ІІ санатты м??алімі Демисенова Гульнар Сииловна
Саба?ты? та?ырыбы: Квадрат те?деуді шешуді? ?дістері.
Саба?ты? ма?саты: 1.Білімділік:Квадрат те?деуд? шешуді? ?рт?рлі тиімді т?сілдерін ?йрету, оларды? ерекшеліктерін танытып, есептер шы?аруда ?олдана білуге ?йрету.
2.Дамытушылы?: О?ушылады? логикалы? ойлау ?абілеттерін дамыта отырып, ой – ?рістерін ке?ейтуге, шы?армашылы?пен ж?мыс істеуге м?мкіндік жасау.
3.Т?рбиелік: Шапша?ды??а, ?з бетімен ж?мыс жасай білуге, ?йымшылды??а т?рбиелеу.
Саба?ты? т?рі: Практикалы?.
Саба?ты? к?рнекілігі: Интерактивті та?та, кубик, ?рт?рлі тапсырмалар.
Саба?ты? жоспары:
1.?йымдастыру б?лімі.
2. Ой тол?ау с?ті.(с?ра?-жауап)
3.Білімі?ді тексер.(де?гейлік тапсырма)
4. «Ойланайы? кім ойшыл?»
5. «Кім жылдам?»(тест)
6. ?орытындылау.
Саба?ты? барысы:
1.?йымдастыру б?лімі.
2. Ой тол?ау с?ті.
Квадрат те?деу туралы не білесі?дер? Ой ?оз?ап білімімізді жина?тайы?.
Квадратты? те?деулер, квадрат те?деуді шешуді? ?дістері, к?бейткіштерге жіктеу, екі м?шені? квадратын айырып алу, формула ар?ылы шешу, виет теоремасы бойынша шешу, графиктік т?сілмен шешу.
3.Білімі?ді тексер.
Топпен ж?мыс істейміз, ?р топтан шы?ып, берілген тапсырманы ?ор?айсы?дар.
І топ. К?бейкіштерге жіктеу, графиктік т?сіл.
ІІ топ. Екім?шені? квадратын айырып алу, коэфиценттеріні? ?асиеттері.
ІІІ топ. Виет теоремасы бойынша.
IV топ. Квадратты? те?деу деп нені айтамыз? Формула ар?ылы шешу.
4.«Ойланайы? кім ойшыл? »
Квадратты? те?деуді ?рт?рлі т?сілмен ?р топтан бір о?ушыдан шы?ып шешу керек.
Х2+8х-9=0
I топ. Екім?шені? квадратын б?ліп алу т?сілі.
ІІ топ. К?бейткіштерге жіктеу т?сілімен.
ІІІ топ. Формула ар?ылы шешу.
IV топ. В иет теоремасын пайдаланып шешу.
5.«Кім жылдам?» Тест.
1) -х2+14х+48 квадрат ?шм?шеден толы? квадратын айыры?ыз.
А) (х+7)2-1 в) (х+7)2+1
С) (х-7)2-1 Д) –(х-7)2+97
2) 2х2-10х+12 квадрат ?шм?шесін к?бейткіштерге жікте?дер.
А) (2х-4)(х+3) В) 2(х-2)(х-3)
С) 2(х+2)(х+3) Д) (х-2)(х-3)
3) х1=25 ж?не х2=-3 деп алып, квадрат ?шм?шені жазы?дар.
А) х2-5,5х+7,5 В) х2-0,5х-7,5
С) х2-5,5х-7,5 Д) х2+0,5х-7,5
4) б?лшегін ?ыс?арты?ыз.
А) С)
В) Д)
5) 7х2-31х-6 те?деуіні? дискриминаитын табы?ыз.
А) 1129 В) 919
С) 793 Д) 1003
6) Берілген те?деулерді? арасынан келтірілген квадрат те?деуді к?рсеті?із.
А) 5х2-29=0 B) -x2+2x-4.8=0
C) x3+x2+12x=0 Д) x2-0,7x-0,75=0
7) 3х2+6,1х-5,4=0 квадрат те?деуін шеші?дер.
А) х1=-2.7; x2= B) х1=2.7; x2=-
C) х1=5.4; x2= Д) х1=5,4; x2=
8) 20х2+х-12=0 те?деуіні? теріс т?бірін табы?дар.
А ) - В) -
С) - Д) -
9) 4х2-9=0 те?деуіні? коэфиценті мен бос м?шесін табы?дар.
А) а=4; в=0; с=9 В) а=-4; в=0; с=9
С) а=4; в=0; с=-9 Д) а=4; в=1;с=9
Бекіту с?ра?тары.
- Квадрат те?деуді? т?бірлеріні? формуласын жаз.
- Дискриминатты ?андай ?ріппен белгілейміз?формуласын жаз.
- Квадрат те?деуді? т?бірлеріні? формуласы.
- Келтірілген квадрат те?деуді? формуласын жаз.
- Толымсыз квадрат те?деуді? формуласын жаз.
?орытынды.
Квадрат те?деуді шешуді? ?рт?рлі ?дістерді ?олдануды? ?тымдылы?ы неде?
Ба?алау.
?й тапсырмасы: №295,№296.
Просмотр содержимого документа
«4»
Сабақтың тақырыбы: Бір айнымалысы бар сызықтық теңдеу.
Сабақтың мақсаты: Білімдік: сызықтық теңдеуді шешу әдістерін меңгерту; теңдеудің шешімдері таба білуге дағдыландыру;
Дамытушылық: Ой – өрісін, ойлау қабілетін дамыту. Шығармашылық ізденіс тапқырлығын, зеректілігін, ойлауға икемділігін дамытуға ықпал ету. Оқушылардың теориялық білімін практикалық шеберлікпен ұштастыру.
Тәрбиелік: Оқушыларды алғырлыққа, шапшаңдыққа, еңбекке, ұйымшылдыққа тәрбиелеу ,ұйымшылдыққа, жинақылыққа еңбекқорлыққа баулу..
Сабақтың түрі: дәстүрлі
Сабақтың типі: жаңа білімді меңгерту
Сабақтың әдісі: көрнекіліктік, сұрақ-жауап.
Пәнаралық байланыс: Қазақ әдебиеті,тарих.
Көрнекілігі: Интерактивті тақта.
Сабақтың барысы: І.Ұйымдастыру.
Оқушылардың сабаққа қатысымы тексеріліп, оқушылар назарын сабаққа аудару.
ІI. Ауызша есептеу
-90-70 -0,4-1,6 2,6-3
:(-4) ∙ (-4) ∙10
∙(-2) -32 ∙ 2,4
+96 : (-2) +100,6
------------ ------------ -----------
? ? ?
Мұнда шыққан сандар нені білдіреді?
ІІІ.Актуалдау.
Біз қазір теңдеулерді шешу барысында қажет болатын жағдайларды қайталаймыз.
1) Жақшаны аш:
3(6-5х) a-(b-c-d) -6(3n+1)
2) Өрнекті ықшамда:
-2∙2,3х 5∙(-6,2а) -2∙(-0,5х)
3) Ұқсас мүшелерді біріктір:
4х-12-2х -6а-2+6а 18-3m-10 0,3x-6-0,2x+2
2. Ауызша сұрау:
1) Теңдеу дегеніміз не?
2) Теңдеудің түбірі деген не?
3) Теңдеуді шешу деген не?
ІҮ. Жаңа сабақ:
Келесі теңдеулердің түбірін табыңдар:
3(х-5)=0 х-5=0 3х=15
Барлығы да х=5
Түбірлері бірдей теңдеулер мәндес теңдеулер делінеді.Ескеретін жағдай кейде теңдеудің түбірлері болмайды.Түбірлері болмайтын теңдеулердің барлығы мәндес теңдеу болады.
Мына теңдеулерге назар аударайық :
5х=-25 -17х=1 3х=0 -2х=-12
Бұлардың барлығы ах=b түріндегі теңдеу, х – айнымалы, а және b – кез-келген сан.
Анықтама: ах=в түріндегі теңдеу бір айнымалысы бар сызықтық теңдеу делінеді.
Мысалы: 3х+0,8 қалай аталады?
-алгебралық өрнек немесе алгебралық қосынды.
Мұндағы 3 саны мен 0,8 санының аталулары?Енді оны мына түрге келтірейік:

 3х+0,8=4х-1,2
3х+0,8=4х-1,2
сол жағы оң жағы
Міне осындай теңдеулер шешу кезінде бір айнымалысы бар сызықтық теңдеуге келтіріледі.
1-қасиет: теңдеудегі қосылғыштың таңбасын қарама-қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді.
2-қасиет: теңдеудің екі жағын да бірдей нөлден өзге бір санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді
Жәутіков Орынбек Ахметбекұлы (1911-1989) - ғалым, физика-математика ғылымдарының докторы, профессор, Қазақстан Ғылым академиясының академигі, Қазақстанның еңбек сіңірген ғылыми және техника қайраткері, Қазақстанның Мемлекеттік сыйлығының лауреаты.Қарағанды облысы Ақтоғай ауданының Қызыларай ауылында дүниеге келген. Негізгі ғылыми еңбектері қозғалыстың орнықтылық теориясына, математика, физика теңдеулеріне, дифференциалдық теңдеулердің шексіз жүйелеріне, теориялық және қолданбалы механикаға, математика тарихы мен оның методологиясына арналған.
Сонымен теңдеулерді шешу үшін: х=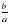
Берілген теңдеулердің шешімдерін табайық:
х=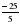 х=
х=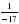 х=
х=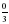 х=
х=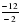
х=-5 х=-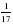 х=0 х=6
х=0 х=6
Жауабы: -5 Жауабы: -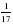 Жауабы: 0 Жауабы: 6
Жауабы: 0 Жауабы: 6
Мысалдар:2,9х+7 = х+1,7; 8х+9= 8х-7 ; 2х+х-5= 3х-5
aх=b теңдеуін шешудің 3 түрлі жағдайы бар:
| а≠0, b≠0 | а=0, b≠0 | а=0, b=0 |
| aх=b x=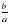 | 0x=b Түбірі жоқ | 0х=0 Шексіз көп шешімі бар |
2х+9=13-х 2х+х=13-9 3х=4 х=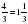 Жауабы:
Жауабы: 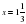
Сонымен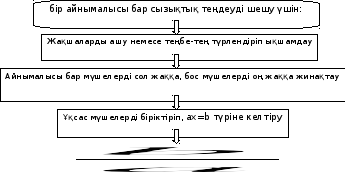 Мысал: 3(х+3)=5х-5 3х+9=5х-5 3х-5х=-5-9 -2х=-14; х=-14 : (-2) х=7
Мысал: 3(х+3)=5х-5 3х+9=5х-5 3х-5х=-5-9 -2х=-14; х=-14 : (-2) х=7
Ү.Бекіту: І тапсырма: Түбірлерін тап:
Теңдеу: 5х=-60; -10х=8; 5х=150; -1,5х=9; -3х=-15
Теңдеу түбірлері: х=-12; х=-0,8; х=30; х=-6; х=5; х=8; х=60; х=-2
ІІ тапсырма: Дұрыс жауабын тап:
3х-1=2(х-2) 3(х+5)=7-5х 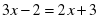
| + (тарих пәнінен ) | + (математика тарихынан) | + (қазақ тілі) |
| Желтоқсан оқиғасының басты тұлғасы Қайрат Рысқұлбековке кейін қандай атақ берілді? | Қазақтан шыққан тұңғыш математик? | Мағыналары бір-біріне қарама-қарсы айтылатын сөздер? |
| а) Халық батыры – х=-15,3 | 1. Жұмаділдаев– х=-8,8 | а) Омоним – х=-1,4 |
| б) Ұлттық батыр – х=9,2 | 2. Жәутіков – х=-1 | а) Антоним – 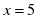 |
| в) Халық қаһарманы – х=-3 | 3. Елубаев – х=3,6 | а) Синоним – х=5,6 |
ІІІ.Оқулықпен жұмыс. (А,В,С деңгейлік тапсырмалар) № 840
В-тобы
№855
1) 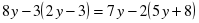
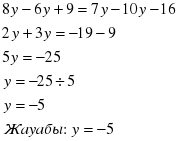
ҮІ. Қорытынды. «Төрт жол өлең»
Теңдік, тәуелсіздік, шешім, таразы тірек сөздерін пайдаланып төрт жол өлең құрау немесе сөйлем жазу.
ҮІІ.Үйге тапсырма. №844 (3,4), №856 (1,2)
ҮІІІ.Бағалау.
Просмотр содержимого документа
«5»
Просмотр содержимого документа
«2»
ІІ санатты мұғалімі Демисенова Гульнар Сииловна
Сабақтың тақырыбы: Квадрат теңдеуді шешудің әдістері.
Сабақтың мақсаты: 1.Білімділік:Квадрат теңдеудң шешудің әртүрлі тиімді тәсілдерін үйрету, олардың ерекшеліктерін танытып, есептер шығаруда қолдана білуге үйрету.
2.Дамытушылық: Оқушыладың логикалық ойлау қабілеттерін дамыта отырып, ой – өрістерін кеңейтуге, шығармашылықпен жұмыс істеуге мүмкіндік жасау.
3.Тәрбиелік: Шапшаңдыққа, өз бетімен жұмыс жасай білуге, ұйымшылдыққа тәрбиелеу.
Сабақтың түрі: Практикалық.
Сабақтың көрнекілігі: Интерактивті тақта, кубик, әртүрлі тапсырмалар.
Сабақтың жоспары:
1.Ұйымдастыру бөлімі.
2. Ой толғау сәті.(сұрақ-жауап)
3.Біліміңді тексер.(деңгейлік тапсырма)
4. «Ойланайық кім ойшыл?»
5. «Кім жылдам?»(тест)
6. Қорытындылау.
Сабақтың барысы:
1.Ұйымдастыру бөлімі.
2. Ой толғау сәті.
Квадрат теңдеу туралы не білесіңдер? Ой қозғап білімімізді жинақтайық.
Квадраттық теңдеулер, квадрат теңдеуді шешудің әдістері, көбейткіштерге жіктеу, екі мүшенің квадратын айырып алу, формула арқылы шешу, виет теоремасы бойынша шешу, графиктік тәсілмен шешу.
3.Біліміңді тексер.
Топпен жұмыс істейміз, әр топтан шығып, берілген тапсырманы қорғайсыңдар.
І топ. Көбейкіштерге жіктеу, графиктік тәсіл.
ІІ топ. Екімүшенің квадратын айырып алу, коэфиценттерінің қасиеттері.
ІІІ топ. Виет теоремасы бойынша.
IV топ. Квадраттық теңдеу деп нені айтамыз? Формула арқылы шешу.
4.«Ойланайық кім ойшыл? »
Квадраттық теңдеуді әртүрлі тәсілмен әр топтан бір оқушыдан шығып шешу керек.
Х2+8х-9=0
I топ. Екімүшенің квадратын бөліп алу тәсілі.
ІІ топ. Көбейткіштерге жіктеу тәсілімен.
ІІІ топ. Формула арқылы шешу.
IV топ. В иет теоремасын пайдаланып шешу.
5.«Кім жылдам?» Тест.
1) -х2+14х+48 квадрат үшмүшеден толық квадратын айырыңыз.
А) (х+7)2-1 в) (х+7)2+1
С) (х-7)2-1 Д) –(х-7)2+97
2) 2х2-10х+12 квадрат үшмүшесін көбейткіштерге жіктеңдер.
А) (2х-4)(х+3) В) 2(х-2)(х-3)
С) 2(х+2)(х+3) Д) (х-2)(х-3)
3) х1=25 және х2=-3 деп алып, квадрат үшмүшені жазыңдар.
А) х2-5,5х+7,5 В) х2-0,5х-7,5
С) х2-5,5х-7,5 Д) х2+0,5х-7,5
4) 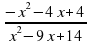 бөлшегін қысқартыңыз.
бөлшегін қысқартыңыз.
А)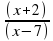 С)
С)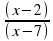
В)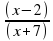 Д)
Д)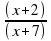
5) 7х2-31х-6 теңдеуінің дискриминаитын табыңыз.
А) 1129 В) 919
С) 793 Д) 1003
6) Берілген теңдеулердің арасынан келтірілген квадрат теңдеуді көрсетіңіз.
А) 5х2-29=0 B) -x2+2x-4.8=0
C) x3+x2+12x=0 Д) x2-0,7x-0,75=0
7) 3х2+6,1х-5,4=0 квадрат теңдеуін шешіңдер.
А) х1=-2.7; x2=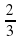 B) х1=2.7; x2=-
B) х1=2.7; x2=-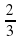
C) х1=5.4; x2=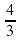 Д) х1=5,4; x2=
Д) х1=5,4; x2=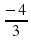
8) 20х2+х-12=0 теңдеуінің теріс түбірін табыңдар.
А ) -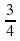 В) -
В) - 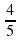
С) -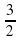 Д) -
Д) -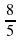
9) 4х2-9=0 теңдеуінің коэфиценті мен бос мүшесін табыңдар.
А) а=4; в=0; с=9 В) а=-4; в=0; с=9
С) а=4; в=0; с=-9 Д) а=4; в=1;с=9
Бекіту сұрақтары.
Квадрат теңдеудің түбірлерінің формуласын жаз.
Дискриминатты қандай әріппен белгілейміз?формуласын жаз.
Квадрат теңдеудің түбірлерінің формуласы.
Келтірілген квадрат теңдеудің формуласын жаз.
Толымсыз квадрат теңдеудің формуласын жаз.
Қорытынды.
Квадрат теңдеуді шешудің әртүрлі әдістерді қолданудың ұтымдылығы неде?
Бағалау.
Үй тапсырмасы: №295,№296.
Просмотр содержимого презентации
«презентация к уроку»

Алгебра. 8 сынып.
Сабақ тақырыбы:
Квадраттық теңдеулерді формула бойынша шешу.

Сабақ мақсаты:
Біліктілік: Квадраттық теңдеулерді формула көмегімен шығаруды үйрету, толымсыз квадраттық теңдеулер туралы алған білімдерін бекіту.
Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру, есеп шығарудың жаңа түрлерін меңгерту және ойдан ой туындатуға, әр сөзді, айтылған ойды дәлелдеуге үйрету.
Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу.

Қайталау сұрақтары
- Қандай теңдеуді квадраттық теңдеу деп атайды?
2. Квадраттық теңдеудегі a, b, c сандары қалай аталады?
3. Қандай теңдеуді толымсыз квадраттық теңдеу деп атайды?
4. Толымсыз квадраттық теңдеулердің неше түрі бар?
5. Толымсыз квадраттық теңдеудің әр түрінің неше түбірі бар болады?
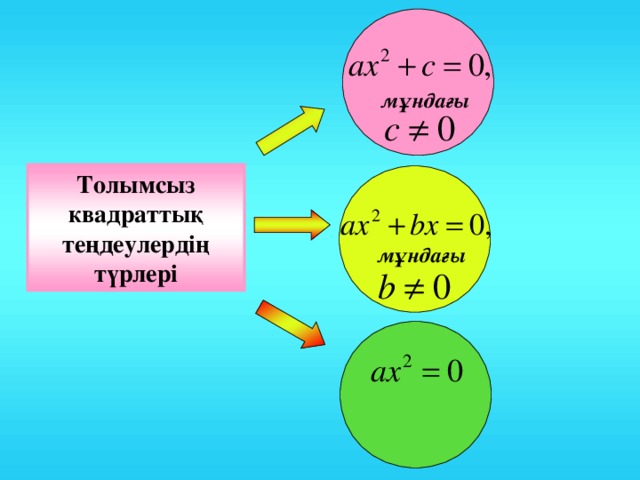
м ұндағы
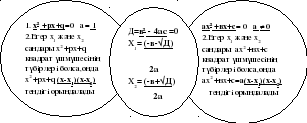
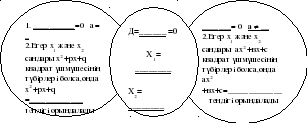
Толымсыз квадраттық теңдеулердің түрлері
м ұндағы
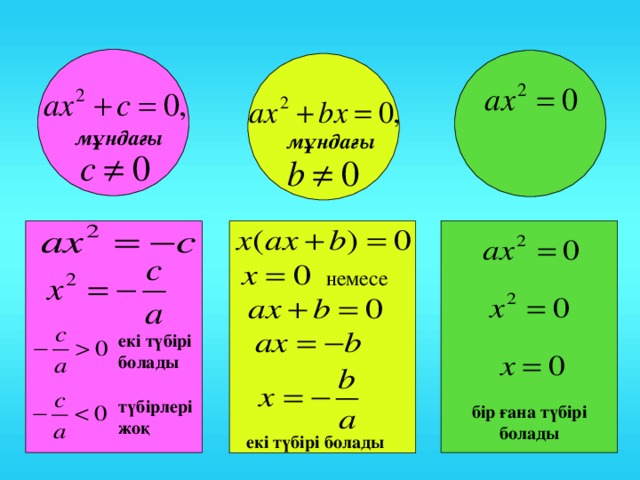
м ұндағы
м ұндағы
немесе
екі түбірі болады
түбірлері жоқ
бір ғана түбірі болады
екі түбірі болады

те ңдеудің екі жағын да -ға бөліп, онымен мәндес болатын келтірілген квадраттық теңдеу шығарып аламыз
Осы теңдеуді түрлендірейік:

те ңдеуімен
те ңдеуі
мәндес. Мұның түбірлерінің саны
бөлшегінің
таңбасына тәуелді болады.
- оң сан болады, сондықтан бұл бөлшектің
болғандықтан,
таңбасы оның алымының, яғни өрнегінің таңбасымен
анықталады. Осы өрнекті квадраттық
теңдеуінің дискриминанты деп атайды . Мұны D әрпімен
белгілейді, яғни Енді екінші теңдеуді
мына түрде жазамыз:

-ға тәуелді мүмкін болатын әр түрлі жағдайларды қарастырайық.
Енді
1. Егер
болса, онда

Сонымен, бұл жағдайда теңдеуінің екі түбірі болады:
Қысқаша былай жазуға болады:
мұны квадраттық теңдеудің түбірлерінің формуласы деп атайды.

2. Егер болса, онда
Бұдан
Бұл жерде теңдеудің бір түбірі болады

3. Егер болса, онда бөлшегінің мәні теріс
болады, сондықтан
теңдеуінің түбірлері жоқ.
Онда теңдеудің де түбірлері жоқ болады.
Сонымен,
екі түбірі болады
бір түбір болады
түбірлері жоқ

1-мысал
Жауабы:

2-мысал
Жауабы:

3-мысал
Жауабы: түбірлері жоқ.

Есеп №1.
Квадраттық теңдеу
a
b
c
Түбірлер
саны

Есеп №2.
Түбірлер
саны
Квадраттық теңдеу
a
b
c
Түбірлері

Деңгейлік тапсырмалар
А
В
В
С
х -тің қандай мәндерінде
х -тің қандай мәндерінде
және
үшмүшесі 1-ге тең мән қабылдайды.
көпмүшелерінің мәндері тең болады.

Тест тапсырмалары
1 . Теңдеуді шешіңіз:
А) 0; 1,5. В) -1,5; 1,5. С) -1,5; 0. D ) 0. Е) 1,5.
2 . Теңдеуді шешіңіз:
А) 0; 1,2. В) -1,2; 1,2. С) -1,2; 0. D ) 0. Е) -1,2.
3 . Теңдеуді шешіңіз:
А) 0; 2. В) -2; 2. С) -2; 0. D ) 0. Е) 2.
4 . Теңдеуді шешіңіз:
А) 1; 6. В) 4; 5. С) 4; 7. D ) -5; 2. Е) -1; 2.
5 . Теңдеуді шешіңіз:
А) 1. В) -1; 0. С) -1; 1. D ) -1. Е) 0.
6 . Теңдеуді шешіңіз:
А) -1; 0. В) Түбірлері жоқ. С) 1. D ) -1. Е) 0.
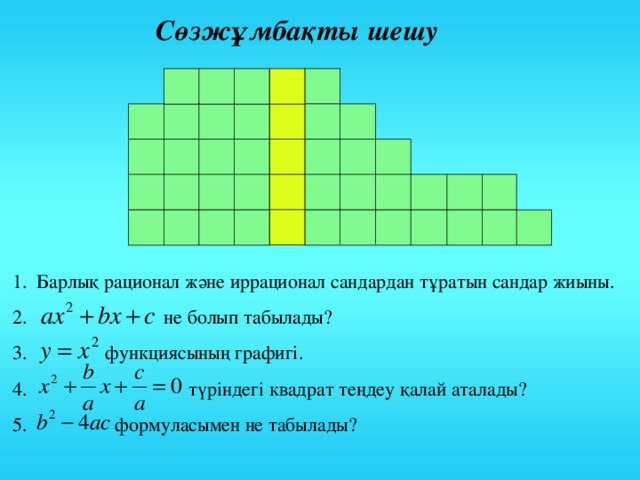
Сөзжұмбақты шешу
- Барлық рационал және иррационал сандардан тұратын сандар жиыны.
- не болып табылады?
- функциясының графигі.
- түріндегі квадрат теңдеу қалай аталады?
- формуласымен не табылады?

Үйге тапсырма:
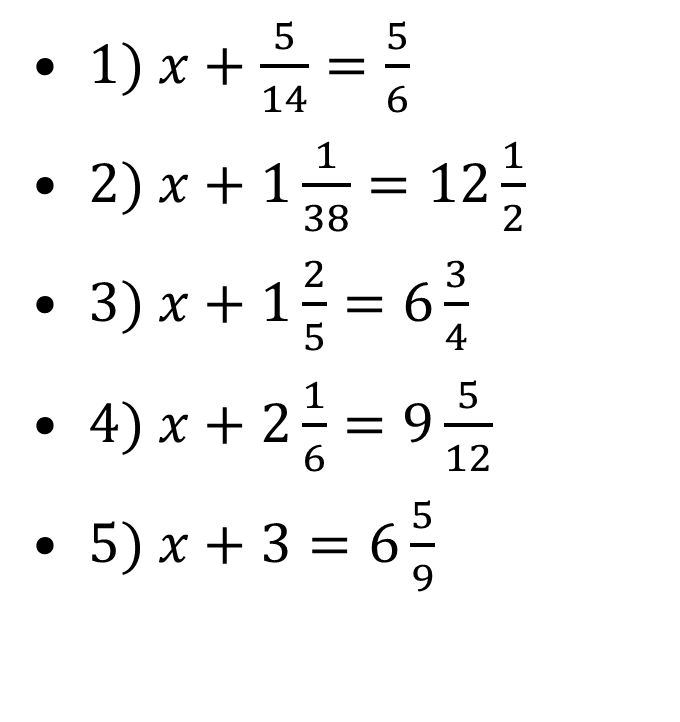
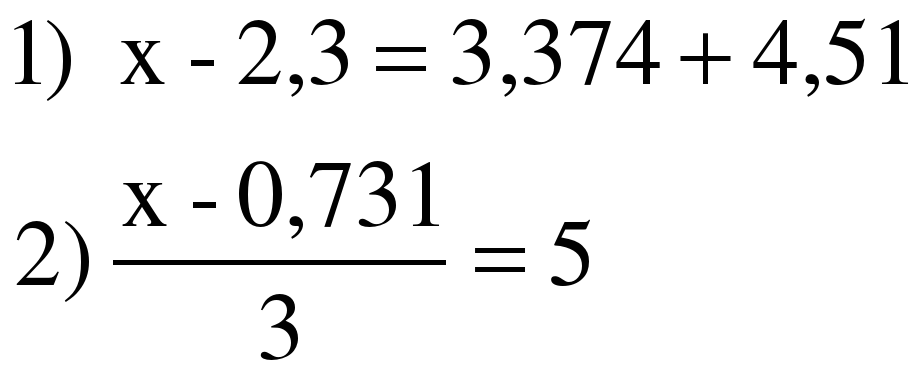
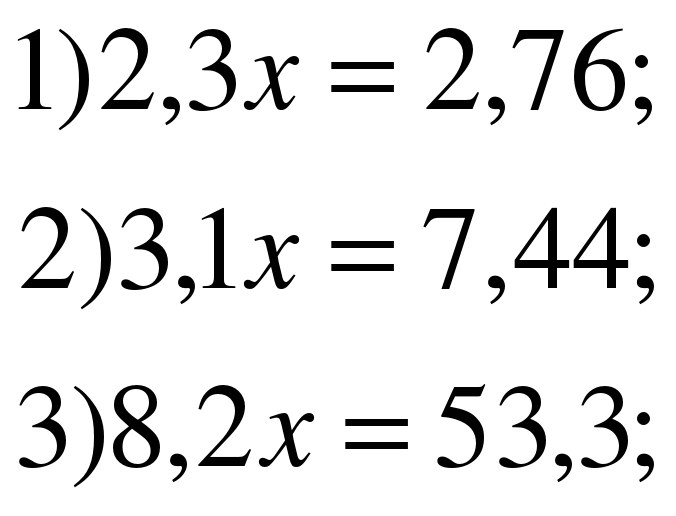
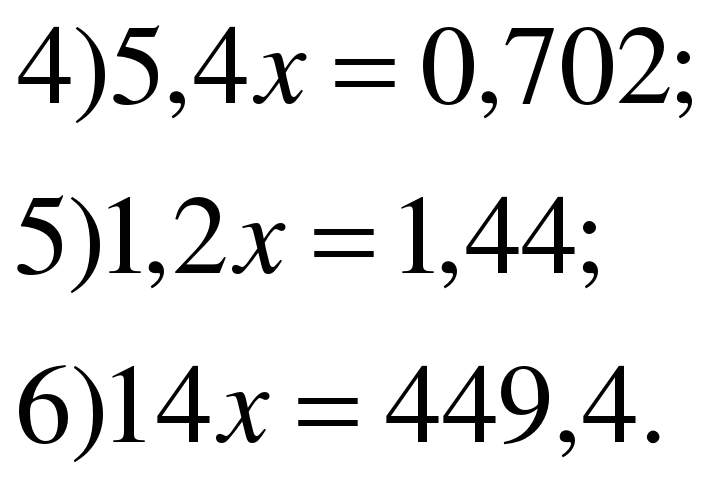



 ефлексия.
ефлексия.

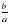
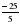 х=
х=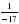 х=
х=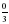 х=
х=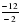
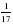 х=0 х=6
х=0 х=6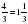 Жауабы:
Жауабы: 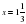
 Мысал: 3(х+3)=5х-5 3х+9=5х-5 3х-5х=-5-9 -2х=-14; х=-14 : (-2) х=7
Мысал: 3(х+3)=5х-5 3х+9=5х-5 3х-5х=-5-9 -2х=-14; х=-14 : (-2) х=7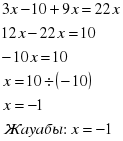
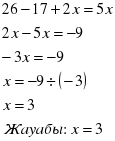
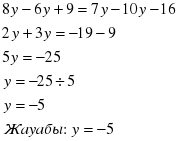
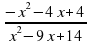 бөлшегін қысқартыңыз.
бөлшегін қысқартыңыз.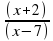 С)
С)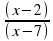
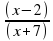 Д)
Д)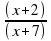
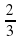
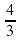
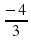
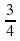 В) -
В) - 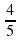
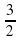 Д) -
Д) -