Акимовка негізгі мектебі » ММ
ГУ « Акимовская основная школа»
Тема урока: «Решение текстовых задач с помощью составления квадратного уравнения»
Подготовила: Гаврилова О.В.
Тема урока: «Решение текстовых задач с помощью составления квадратного уравнения»
Цели урока:
Образовательные.
Задачи урока:
Развивающие.
способствовать умению анализировать условие задач, развитию умения рассуждать, развитию познавательного интереса, умению видеть связь между математикой и окружающей жизнью;
формировать умения чётко и ясно излагать свои мысли;
развивать эмоции учащихся через создание на уроке ситуаций эмоциональных переживаний;
Воспитательные.
Воспитывать умение работать с имеющейся информацией в необычной ситуации;
Воспитывать уважение к предмету, умение видеть математические задачи в окружающем нас мире;
воспитывать внимательность и культуру мышления, самостоятельность и взаимопомощь.
Тип урока: закрепление и расширение ранее полученных знаний.
Форма урока: практикум.
«Уравнение - это золотой ключ, открывающий все математические сезамы».
С. Коваль
Ход урока:
Организационный момент. Вступительное слово учителя (презентация).
Добрый день дорогие ребята! Я рада приветствовать Вас на нашем уроке, и прошу всех вас улыбнуться друг другу и нашим гостям, мысленно пожелать успехов и себе и товарищам. Я хочу немного подсластить наш урок и угостить вас конфетеми. Разбейтесь на группы по цвету фантика.
Мне хочется начать наш урок со слов французского философа Ж.Ж. Руссо (1712-1778гг): « Вы талантливые дети! Когда-нибудь Вы сами приятно поразитесь, какие Вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…» Я желаю Вам уже сегодня убедиться в этих словах.
Тема сегодняшнего урока: “Решение текстовых задач с помощью составления квадратного уравнения”.
Испокон века
Книга растит человека
Урок – это книга, которую можно с интересом читать, перелистывая страницу за страницей, обогащаясь знаниями, «расти» умом. Сегодня мы с вами продолжим читать главу «Квадратные уравнения» − очень важную для изучения курса математики. Будем совершенствовать навыки решения задач; Выработаем умение применять квадратные уравнения для решения алгебраических и геометрических задач; Покажем не только знания, но и свои умения, навыки по этой теме.
Слайд 2. Великий, немецкий ученый А. Эйнштейн говорил о себе: “Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только до данного момента, а уравнения будут существовать вечно”.
Откройте пожалуйста тетради и запишите сегодняшнее число, классная работа.
Актуализация опорных теоретических и практических знаний (слайды ).
Что написано на доске? ах2 + bх + с = 0 (Квадратное уравнение)
Всегда ли имеет корни квадратное уравнение? (Нет, не всегда)
От чего зависит количество корней? (От дискриминанта)
Сколько корней имеет квадратное уравнение, если D 0?
Сколько коней имеет квадратное уравнение если D = 0?
Сколько корней имеет квадратное уравнение, если D
Чему равно: 2 в квадрате?
3 в квадрате?
5 в квадрате?
Угол в квадрате? ( в квадрате все углы прямые).
Итак, ребята, давайте повторим основные понятия и формулы для решения квадратных уравнений. Я предлагаю вам написать математический диктант по теме “квадратные уравнения”.
Математический диктант. (Cлайды )Приложение №1
Ответы на вопросы диктантов записываем на бланках ответов (приложение 3). Записывать только коротко ответы. У каждого варианта будет по 6 вопросов.
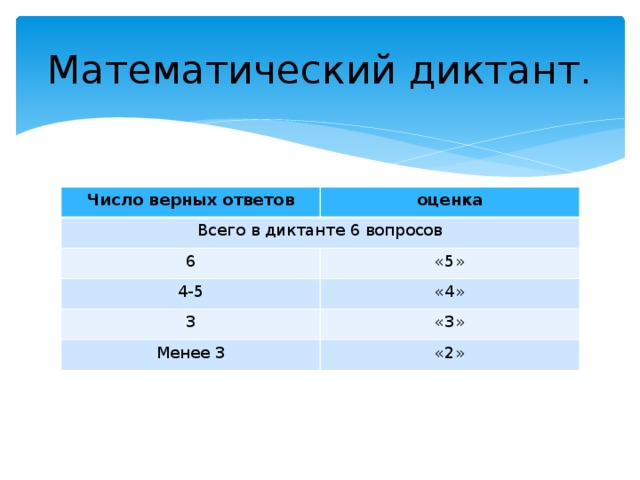
Норма выставления оценок:
| Число верных ответов | Оценка |
| Всего в диктанте 6 вопросов |
| 6 | “5” |
| 5-4 | “4” |
| 3 | “3” |
| менее 3 | “2” |
1.1. Сформулируйте определение квадратного уравнения.
2.1. Какое уравнение называют неполным квадратным уравнением.
1.2. Запишите пример неполного квадратного уравнения.
2.2. Запишите пример квадратного уравнения.
1.3. Запишите, чему равен второй коэффициент в уравнении: 2х2 + х – 3 = 0.
2.3. Запишите, чему равен первый коэффициент в уравнении: -х2 + 4х – 7 = 0.
1.4. Запишите, чему равны: a, b, c в уравнении: - 3х2 + 5х = 0.;
2.4. Запишите, чему равны: a, b, c в уравнении: 5х2 - 8= 0.
1.5. Сколько корней может иметь неполное квадратное вида ах2 + с = 0?
2.5. Сколько корней может иметь неполное квадратное вида ах2 + bх = 0?
1.6. Сколько корней имеет квадратное уравнение, если дискриминант положительный?
2.6. Сколько корней имеет квадратное уравнение, если дискриминант отрицательный?
Давайте проверять ваши работы. Обмениваемся своими бланками ответом с соседом по парте. И сравниваем ваши ответы с ответами на доске (слайд 20). Против правильного ответа ставим “+”, против ошибочного - “-”, если в ответе есть недочет, можно поставить “±”. Выставляем отметки и возвращаем бланки обратно.
Правильные ответы( Слайд):
1. Квадратным уравнением называется квадратное уравнение вида ах2 + bх + с = 0, где х – переменная, а, b, с – некоторые числа, причем а ? 0.
2.1. квадратное уравнение ах2 + bх + с = 0, в котором хотя бы один из коэффициентов b или c равен 0.
1.2. пример 5х2 -4х = 0 или 4х2 – 9 = 0.
2.2. пример 14х2 – 5х – 1 = 0.
1.3. 1
2.3. – 1
1.4. а = - 3, b = 5, с = 0.
2.4. а = 5, b = 0, с = - 8.
1.5. два или не имеет корней.
2.5. два.
1.6. два.
2.6. не имеет корней.
Учитель собирает работы, проходя по классу, сразу по вариантам, чтобы облегчить работу.
Задание: приложение №2
Составьте квадратное уравнение, используя следующие данные:
А) Многие, уходя из кабинета, не выключают свет. Да и дома порой зажигают все лапы, когда в этом нет необходимости. Кто-то может сказать: мелочь! Между тем сосчитайте, сколько за 10 часов расходует одна лампочка в 100 Вт. Ответ переведите в кВт. Полученное число будет первым коэффициентом квадратного уравнения. Ответ: 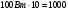 Вт =1кВт, а =1.
Вт =1кВт, а =1.
Б) А что такое капля воды из неплотно закрытого крана? За час теряется 0,6л, а за сутки – .. ? (14,4л воды). В данном числе сложите цифры. Полученное число будет вторым коэффициентом. Ответ: 14.4л, 1+4+4 = 9, в=9.
В) К обеду школа получает 35 кг хлеба, в бачках для отходов остаётся 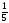 часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом.
часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом.
Ответ: 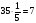 ,
, 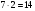 , с=14.
, с=14.
Г) Все коэффициенты положительные числа. Составьте квадратное уравнение, решите его. Ответ: у2+9у+14=0; D=25, у1,2= 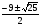 ; у1 = -7,у2 = -2.
; у1 = -7,у2 = -2.
Изучение нового материала( Слайд):
Учитель: Многие задачи алгебры, геометрии, физики приводят к необходимости решения квадратных уравнений. Мы с вами должны научиться проводить анализ задачи, вводить неизвестные величины, находить зависимость между данными задачи и неизвестными величинами.
Задача №1. После выпуска из школы ученики обменялись фотографиями на память. Сколько было выпускников, если они обменялись 870 фотографиями?
Решение.
Сопровождающие вопросы:
О чём говорится в задаче?
Что известно в условии задачи?
Что нужно найти в задаче?
Каким способом можно решить задачу?
Что обозначим за переменную?
Пусть было х учеников, тогда они обменялись (х-1) фотографиями, т.к. ученик сам с собой фотографией не обменивается. Так как всего обменялись 870 фотографиями, то составим уравнение: x(x-1)=870
х=30 и -29
Что обозначили за x?
Все ли решения уравнения будут решением задачи? (-29 не удовлетворяет смыслу задачи) Почему?
Итак, мы рассмотрели решение текстовой задачи с помощью квадратного уравнения.
1. Задача Бхаскары (знаменитый индийский математик XII века):
Решить задачу: «Обезьянок резвых стая,
Всласть поевши, развлекалась.
Их в квадрате часть восьмая,
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
Решение. x – число обезьян, тогда (х/8)2 + 12 = х, х2/64 − х + 12 = 0, х2 − 64х + 768 = 0.
D1 = 1024 − 768 = 256, х1 = 16, х2 = 48.
Ответ: 16 или 48.
4.Физкультминутка.
Коль писать мешает нос,
Значит, это сколиоз
Вас сгибает над тетрадкой,
Позвоночник не в порядке.
Мы ему сейчас поможем:
Руки за голову сложим,
Повороты влево – вправо,
И наклоны влево – вправо,
Ручки к солнцу потянулись,
Мы назад ещё прогнулись,
Повращаем мы плечами,
Чтоб они не подкачали.
Улыбнулись всем, кто рядом.
Вот! Уже другой порядок!
А теперь повыше нос:
Нам не страшен сколиоз.
Сядем ровно, ручки – в руки,
Продолжаем путь к науке.
5. Задание каждой группе: «Зигзаг» - восстановить последовательность этапов алгоритм решения текстовой задачи
| «Зигзаг» (Приложение №3) | Правильный ответ |
| 1.Установить связь известных фактов с неизвестными 2.Записать ответ 3.Внимательно изучить условие задачи 4.Исключить корни уравнения, неудовлетворяющие смыслу задачи 5.Ввести переменную 6.Решить полученное уравнение 7.Вернуться к вопросу задачи, сделать необходимые вычисления (при необходимости) 8.Составить уравнение, исходя из смысла условия задачи 9.Выяснить, что известно в задаче Ответ: 391586472 | Внимательно изучить условие задачи Выяснить, что известно в задаче Установить связь известных фактов с неизвестными Ввести переменную Составить уравнение, исходя из смысла условия задачи Решить полученное уравнение Исключить корни уравнения, неудовлетворяющие смыслу задачи Вернуться к вопросу задачи, сделать необходимые вычисления (при необходимости) Записать ответ |
Обсуждение, выявление ошибок, коррекционная работа
Выдача каждой группе готового алгоритма решения текстовой задачи
6.Решешие задач приложение №4
Каждая группа получает задачу с решением, в котором есть пропуски, которые необходимо заполнить (приложение №4):
| 1 группа Первое число больше другого на 10. Найдите эти числа, если их произведение равно 56. Уравнение: x(x+10)=56 Корни: -14; 4 | 2 группа Ширина прямоугольника на 3 см меньше его длины. Найдите ширину и длину прямоугольника, если их площадь равна 130 см2 Уравнение: x(x-3)=130 Корни: -10; 13 |
Стратегия «Карусель» - по часовой стрелке в периодом в 3 минуты один ученик переходит в соседнюю группу, чтобы объяснить решение свой задачи другим учащимся
После «Карусели» у учащихся в тетради должно быть по 2 задачи
7.Работа с оценочным листом (рефлексия)
Выполнение индивидуального задания (приложение №1: оценочный лист)
Работа с критериями успешности
Написание комментария по итогам урока, изложение оставшихся вопросов по теме
Что мы сегодня повторили на уроке?
А что нового мы с вами сегодня узнали на уроке?
Кто доволен своей работой сегодня?
Какой этап урока вам понравился больше всего?
Хочется отметить, что никто из Вас не отнесся к работе равнодушно, и если у кого-то не всё получилось, не огорчайтесь: “Дорогу осилит идущий ”.
8.Подведение итогов урока
9.Постановка д/з, инструктаж
Задача 1. Сумма цифр двузначного числа равна 8. Если цифры этого числа переставить, то получится число, меньшее искомого на 18. Чему равно искомое число? Ответ: 53
Задача 2. Составьте уравнение к задаче, приняв за х меньшее из чисел: Одно из чисел на 12 больше другого, а их произведение равно 315. Найдите эти числа.
Задача 3. Один из катетов прямоугольного треугольника на 6 см меньше гипотенузы, а другой на 3 см больше первого. Найдите гипотенузу, если площадь треугольника равна 54 см2.
 Ответ:
Ответ: 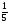 часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом.
часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом. 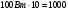 Вт =1кВт, а =1.
Вт =1кВт, а =1.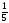 часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом.
часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом. 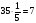 ,
, 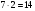 , с=14.
, с=14.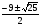 ; у1 = -7,у2 = -2.
; у1 = -7,у2 = -2.






 0 ? Сколько корней имеет квадратное уравнение, если D = 0 ? Сколько корней имеет квадратное уравнение, если D = 0 ? Чему равно: 2 в квадрате? 3 в квадрате? 5 в квадрате? Угол в квадрате?" width="640"
0 ? Сколько корней имеет квадратное уравнение, если D = 0 ? Сколько корней имеет квадратное уравнение, если D = 0 ? Чему равно: 2 в квадрате? 3 в квадрате? 5 в квадрате? Угол в квадрате?" width="640"