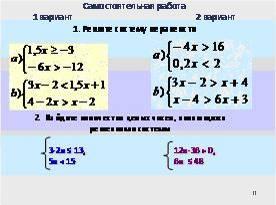Технологическая карта к уроку алгебры 8 класса "Решение систем неравенств с одной переменной"

Личностные

Метапредметные

Предметные

Умение аргументировать свою точку зрения, общаться в коллективе, слушать собеседника и вести диалог.

Развивать активность и находчивость при решении задач,.

Увидеть роль и место математики в других дисциплинах и окружающей жизни;

уметь обрабатывать информацию; выбирать способы решения неравенств в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности

уметь решать линейные неравенства и системы;

графически изображать множество их решений, а также записывать решения в виде числового промежутка;

производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение).

№

Этап

УУД

Деятельность

ИКТ, наглядность

Время

Учителя

Обучающегося

1.

Организационный

Регулятивные УУД

Структурирование знаний;

Прогнозирование;

Формулирование проблемы;

Целеполагание;

Коммуникативные УУД:

Умение выражать свои мысли;

Личностные УУД: Умение выделять нравственный аспект поведения

Познавательные УУД:

Поиск и выделение информации;

Смысловое чтение;

Построение логической цепи рассуждений;

Структурирование знаний;

Выдвижение гипотез и их обоснование

Коммуникативные УУД:

Учебное сотрудничество;

Регулятивные УУД

Коррекция-внесение необходимых дополнений и корректив.

Регулятивные УУД

Оценка-выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

Познавательные УУД:

Поиск и выделение необходимой информации. Структурирование знаний.

Построение логической цепи рассуждений. Осознанное и произвольное построение речевого высказывания в устной форме;

Регулятивные УУД

Оценка-выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

Планирование, прогнозирование

Личностные УУД:

Развитие познавательных интересов.

Регулятивные УУД

Планирование своей деятельности в группе для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция

Коммуникативные УУД:

Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в обсуждении

Регулятивные УУД

Планирование своей деятельности в группе для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция

Коммуникативные УУД:

Планирование учебного сотрудничества со сверстниками; участие в обсуждении

Личностные : развитие критического (креативного) мышления, умения логического построения выводов, гипотез, умение находить и доказывать ошибки.

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.

Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД

Приветствую учащихся,

организую начало урока.

(Двух учеников вызываю – становятся слева и справа. Показываю коробку (с одной стороны желтая, с другой красная. ) Что это ? (Если необходимо, задаю наводящие вопросы). Вы можете достоверно и правильно сразу ответить на этот вопрос? а что нужно сделать, чтобы точно ответить на мой вопрос?

Как вы думаете, уважаемые философы, что я хотела этим опытом вам сказать?

Напомните тему, которую мы изучаем и попробуйте сформулировать цель и задачи урока.

Записываем в тетрадях тему урока, число сегодняшнее.Попробуйте поставить себе прогнозируемую оценку за урок.

Приветствуют учителя, настраиваются на урок

Высказывают разное- то, что видят со своей стороны.

«Нужно посмотреть со всех сторон, а еще внутрь заглянуть- что там находится?»

Чтобы правильно ответить на вопрос, на проблему нужно взглянуть со всех сторон,- чтобы получить верное представление.

Формулируют тему урока, цель урока.

Ставят оценки в лист самооценки.

Презентация

(Слайд 1)

Слайд2

2 мин.

2.

3

4

5

6

7

8

9

10

11

12

Мотивация и актуализация знаний

Проверка домашнего задания

Применение знаний

Решение проблемного вопроса

Восприятие и осмысление учащимися нового материала.

Проверка пониманий.

Физминутка

Решение задач из ОГЭ

Небольшая интеллектуальная пауза

Рефлексия (подведение итогов урока)

Синквейн

Информация о домашнем задании, инструктаж по его выполнению.

Самостоятельная работа (если осталось время)

Для повторения теории темы, ее понимания и умения применять проведем тестирование с последующей проверкой и беседой по теории темы. Поиграем в «Верю - не верю». Каждое задание теста предполагает ответ «Да» или «Нет». «Да» -1 «Нет» - 0.

В результате выполнения теста получится какое-то число.

Вопросы теста:

1)Является ли число 12 решением неравенства 2х10?

2) Является ли число -6 решением неравенства 4х12?

3) Является ли неравенство 5х-154х+14 строгим?

4) Существует ли целое число принадлежащее промежутку [-2,8;-2,6]?

5) При любом ли значении переменной а верно неравенство а² +4 о?

6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?

Кто смог решить дома № 883? Такие задания встречаются на ОГЭ.

Постановка проблемы: что такое допустимые значения переменной и как решать задачи на нахождение допустимых значений переменной?

Давайте вместе проанализируем и применим наш прием «З - Х- У» («З»- знаем, «Х- хотим узнать, «У»-узнали

- Что мы знаем?

Устные дополнительные вопросы

1.Сформулируйте основные свойства неравенств, используемые при решении и доказательстве неравенств и их систем?

2.Что называется решением системы неравенств?

3.Алгоритм решения системы неравенств?

(Уточнить алгоритм - на слайде)

- Что мы хотим узнать?

- Ну а на вопрос «Что узнали?» ответим позднее.

Применим наши знания для решения задач. Решаем по группам №882 и передаем другой группе на проверку или дополнение.

Вернемся к № 883. Кто пойдет к доске?

– Сколько ограничений надо учесть?
– Они должны выполняться одновременно?
– Вы знакомы с символом, который в алгебре указывает на одновременное выполнение заданных условий? (Это знак системы).

- А вот в № 884 стоит вопрос «Найти область определения». Это чем-то отличается от предыдущего вопроса, как вы думаете, или нет?

Несколько упражнений для отдыха и разминки перед следующей работой

Работа с заданиями из ОГЭ по данной теме на применение полученных знаний (групповая работа)

1 ученик демонстрирует математический софизм- докажет нереальное неравенство. Вначале возьмем верное неравенство

65. Так? Умножим обе части неравенства на 5, а потом из обеих частей вычтем 6². 6*5- 6 ² 5*5- 6 ² . Пока все правильно? Вынесем слева общий множитель за скобки 6(5-6), а справа разложим по формуле разности квадратов, получим: 6(5-6) (5-6)(5+6). Теперь обе части сократим на скобку (5-6), получим 611. Где ошибка?

-Что нового узнали сегодня на уроке?

-Кто хорошо понял тему ?

-Кому нужно еще потренироваться?

Давайте продумаем синквейн к данному уроку. Итак, понятие «Система неравенств». Составьте 2 прилагательных к нему, три глагола, выразите чувство или крылатую фразу, а также синоним.

А я к синквейну и нашей теме подобрала слова писателя Александра Володина. Надеюсь, вы правильно их поймете и сделаете какой-то вывод для себя.

Сегодня мы говорили о решении систем неравенств с одной переменной. На следующем уроке мы продолжим и научимся решать двойные неравенства Еще раз повторите теоретический материал п.35 стр. 184-187 и решите

№ 885(а,б) – 883(г).

Спасибо всем за урок!

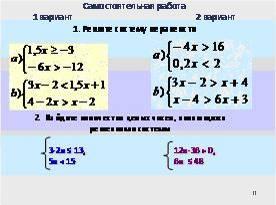
Слушают учителя.

Учащиеся устно выполняют предложенные задания, записывают ответы в виде 1 и 0.

Самопроверка

Ставят оценки в лист самооценки в №1.

2 ученика (из «слабых») на доске пишут «Памятку-шпаргалку»

Фронтальная работа

Ответы учащихся:

1.Мы знаем как решать неравенства

2.Как решить систему неравенств.

3.Как записать промежутки, которые являются решением неравенства или системы

Самопроверка

Ставят оценки в лист самооценки в №2.

- Как находить допустимые значения выражения?

Групповая работа и методика «Карусель».

Каждый ставит себе оценку в № 3 за работу в группе.

Решают задачу, анализируют, высказывают свое мнение, делают вывод

Вступают в диалог, составляют неравенства

Делают упражнения

Выполняют сначала индивидуально, затем в группе обсуждают и выдают общий ответ.

Высказывают свое мнение.

Каждый ставит себе оценку в № 4 за работу

Отвечают на вопросы своего товарища, пытаются найти ошибку в доказательстве неравенства.

Отвечают на вопросы

Выставляют себе итоговые оценки за урок

Составляют, придумывают слова к синквейну с понятием «система неравенств» или проще к слову «неравенство»

Записывают домашнее задание

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

5 мин.

7 мин.

10 мин

4 мин

7 мин

5 мин

3 мин

2 мин