| 1. Мотиваци онно-организацион ный момент | Ребята, урок я начну с высказывания Г.Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать». Я хочу, чтобы вы на уроке думали и рассуждали. | Учащиеся настраиваются на работу | Создание эмоционального настроя на урок | КУУД: планирование учебного сотрудничества с учителем и сверстниками |
| 2. Актуализация знаний | Какую тему мы проходили на прошлом уроке? Координаты вектора Какие вектора называются координатными? Какие вектора наз. коллинеарными? коллинеарны ли единичные вектора? (нет). Значит, можно любой вектор разложить по координатным вектора. Запишите это разложение. Как называются коэффициенты разложения? (координатами данного вектора). В каких скобках записываются координаты вектор? (в фигурных).
Откройте тетради и запишите дату. Классная работа. 1. Выпишите координаты вектора 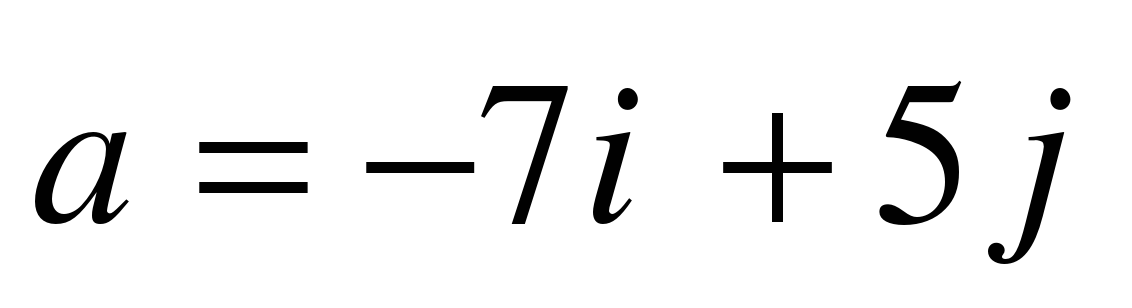 ; ; 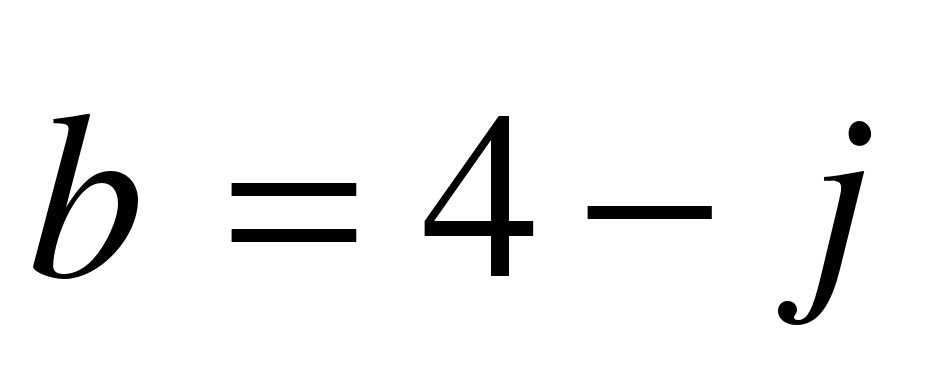 2. Запишите разложение по координатным векторам 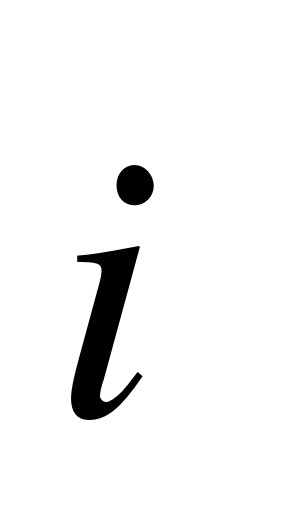 и и 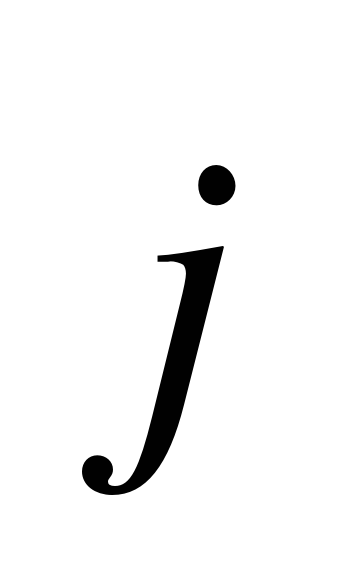 : : 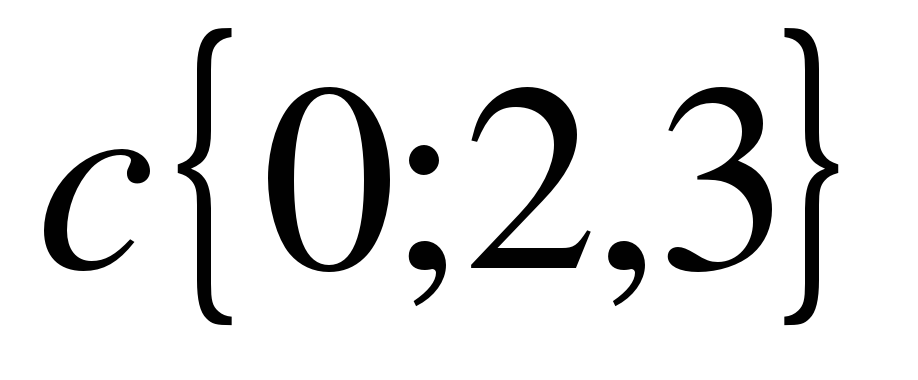 ; ; 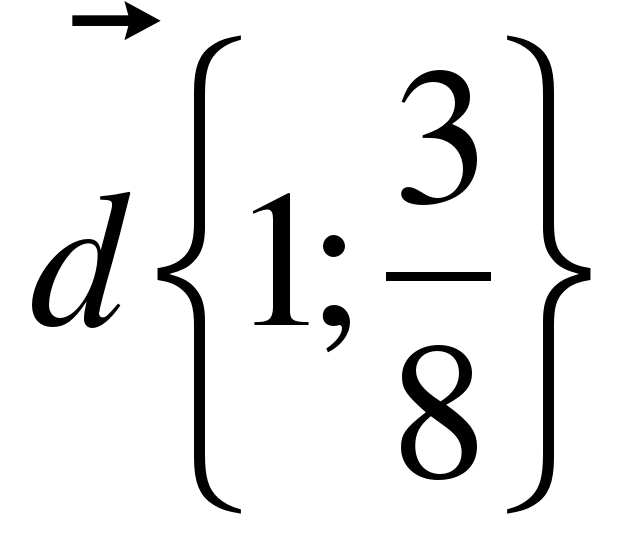 | Отвечают на вопросы и записывают основную систему понятий в тетради | Выявляет уровень знаний. Определяет типичные недостатки | РУУД: - оценка (выделение и осознание обучающимся того, что уже усвоено и что нужно усвоить; оценка результатов работы).
ПУУД: осуществлять анализ, синтез, сравнение, делать выводы Формы работы: фронтальная. Система оценивания: самоконтроль
|
| 3. Постановка учебной задачи | Какую цель мы ставили на этот урок? Применение знаний для решения простейших задач методом координат. Итак, цель сегодняшнего урока? Тема урока та же? Да, метод координат. Запишите тему урока.
| Выделяют известную часть и неизвестную. Ставят цель урока, формулируют тему урока | Создает проблемную ситуацию. Побуждает к формулированию цели. | ЛУУД: формирование готовности к сотрудничеству; РУУД: целеполагание (постановка учебной задачи на основе того, что известно и, что еще неизвестно); ПУУД: общеучебные: самостоятельное выделение - формулирование цели; логические: формулирова- ние проблемы. |
| 4-5. Решение учебной задачи (построение проекта выхода из затруднения). Первичное закрепление | (Ученик у доски посильнее) 1. Дано:  , , 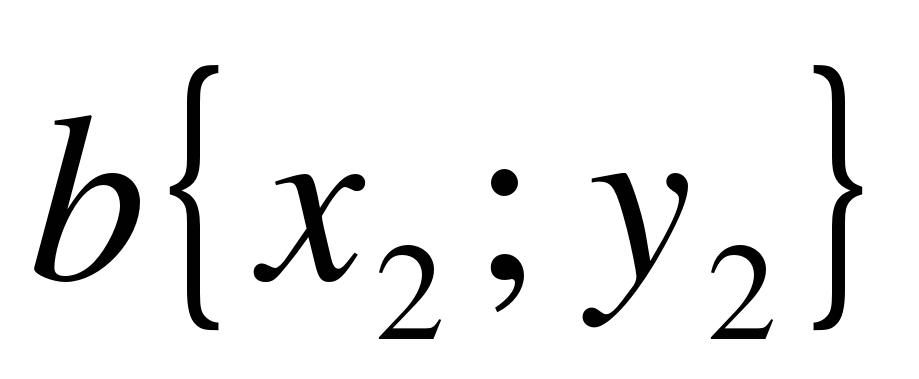 Доказать:  Доказательство: (наводящий вопрос: как данные вектора разложить по координатным векторам  и и 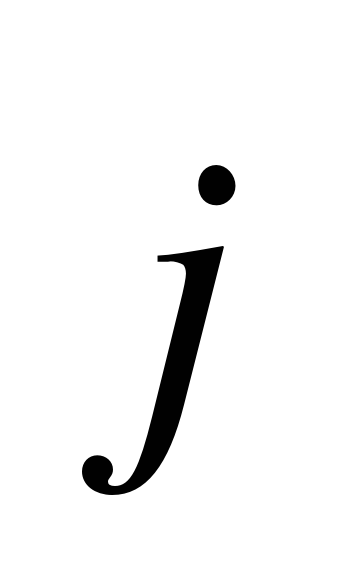 ). ). 
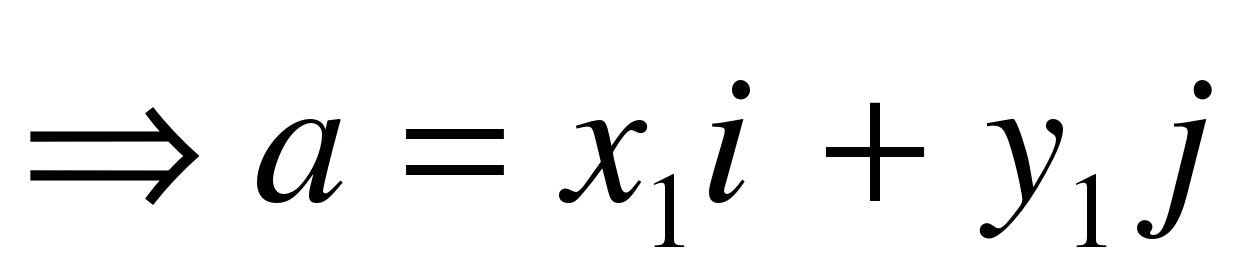 , ,
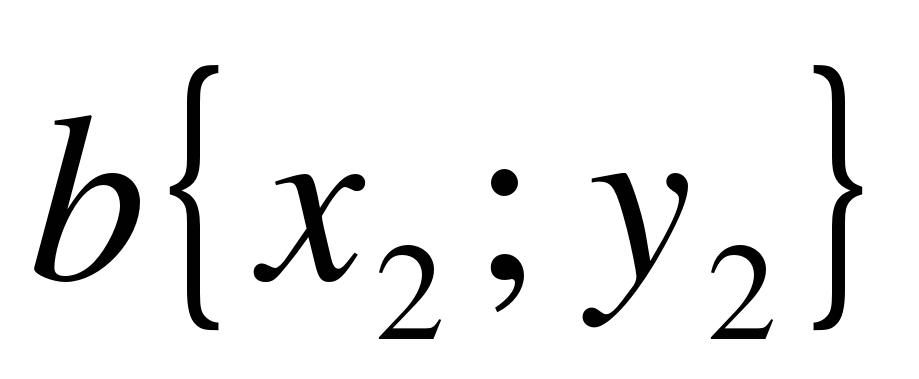
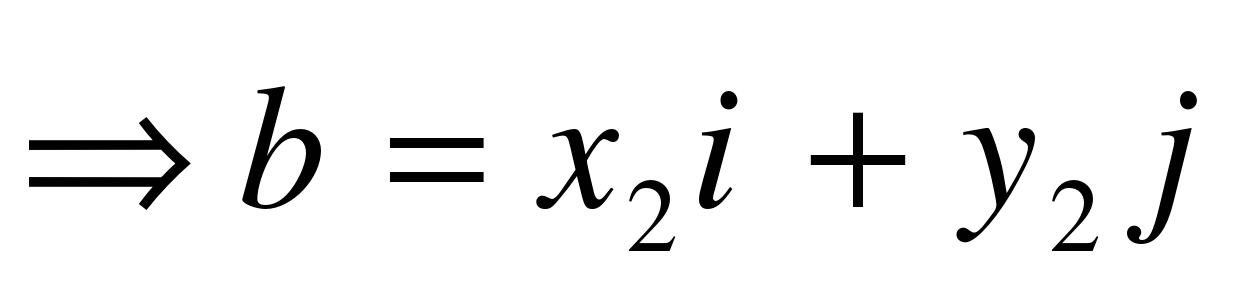 , ,
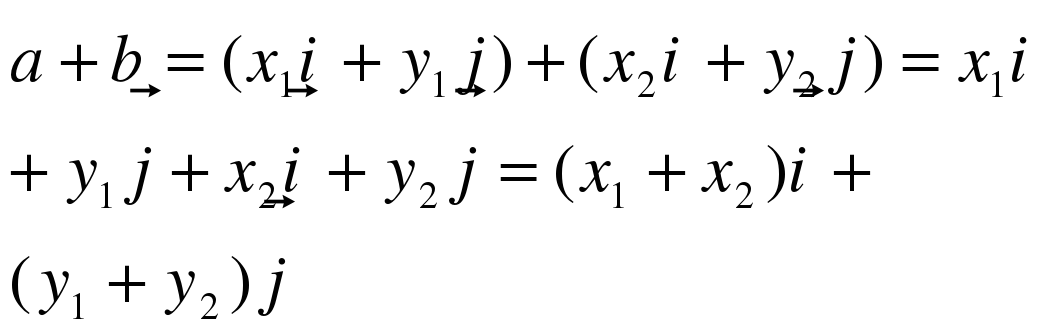 Вывод: Координаты суммы двух векторов: Вывод: Координаты суммы двух векторов:  . Что и требовалось доказать. Скажите, а это правило можно применять только для суммы двух векторов? Да. . Что и требовалось доказать. Скажите, а это правило можно применять только для суммы двух векторов? Да.
Сформулируйте правило нахождения каждой координаты суммы двух или более векторов: Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Проговорите правило вслух; шепотом; про себя; друг другу.
(2 ученик, послабее): № 922 (в)
2. Дано:  , , 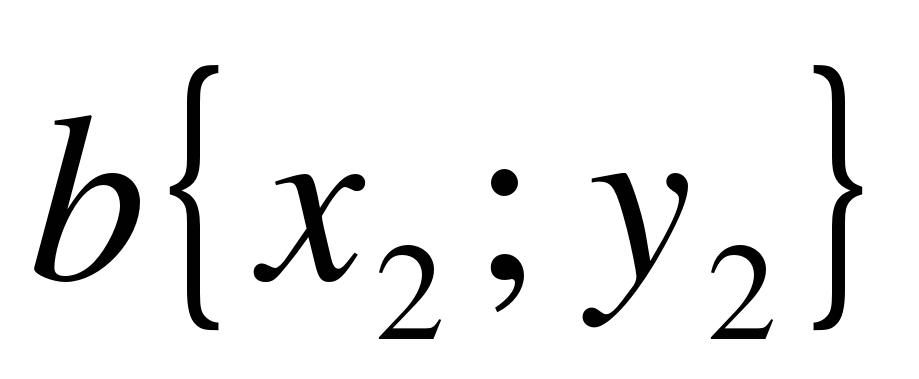 Доказать:  Дать 2-3 минуты на обдумывание доказательств в парах, одного из учащихся попросить выполнить задание за доской, а затем заслушать всем классом его решение и обсудить правильность решения Доказательство:  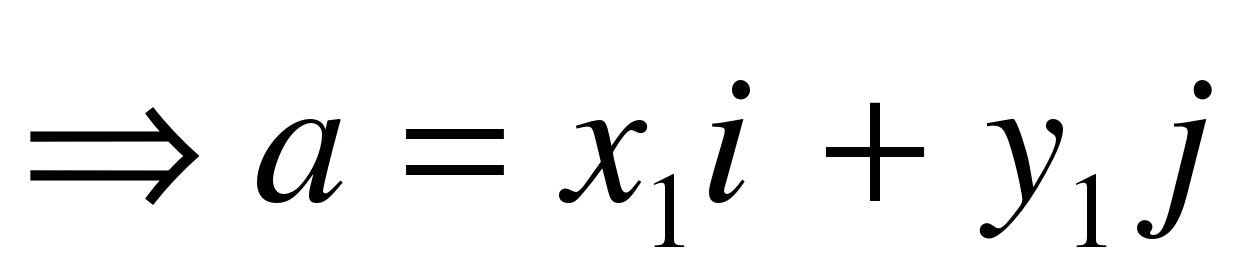 , ,
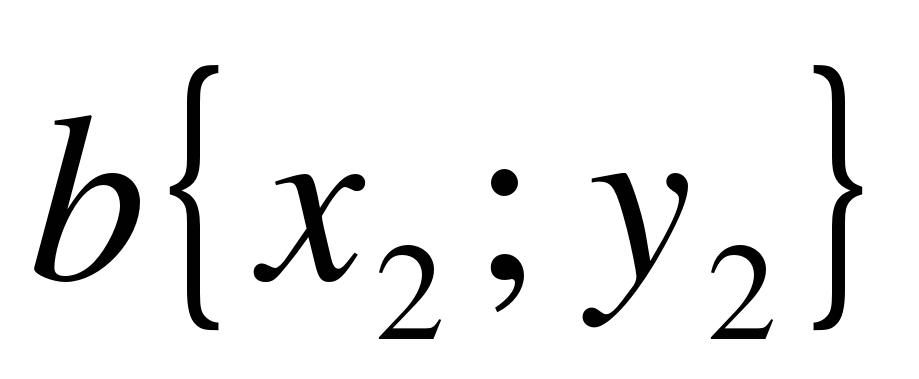
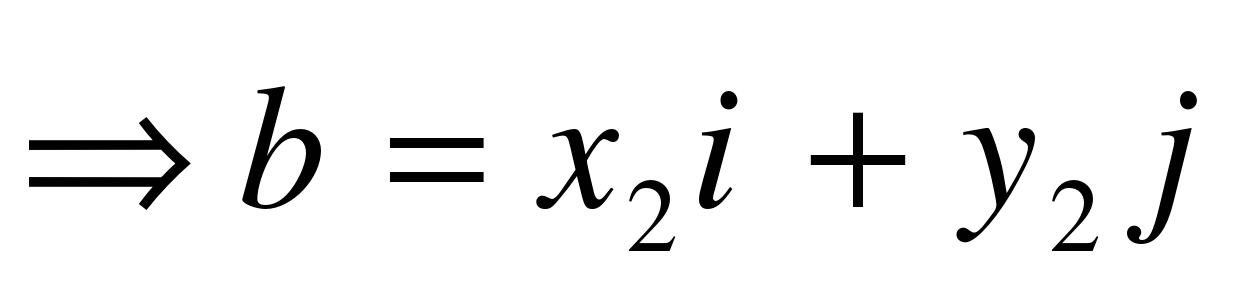 , ,
 Вывод: Координаты разности двух векторов: Вывод: Координаты разности двух векторов: 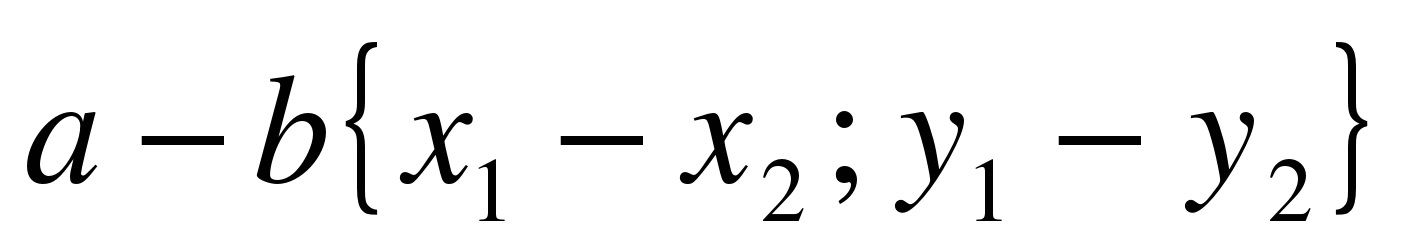 . Что и требовалось доказать. . Что и требовалось доказать.
Сформулируйте правило нахождения каждой координаты разности двух векторов: Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Проговорите правило вслух; шепотом; про себя; друг другу. ( 4 ученик за доской): № 923 (г) 3. Дано: 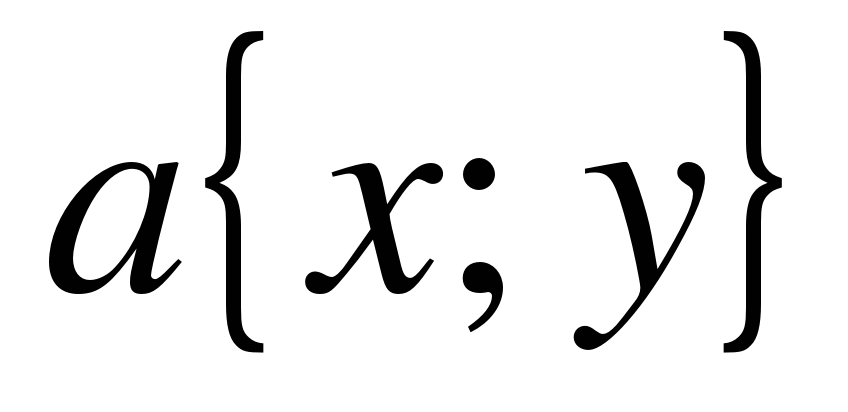 Доказать: 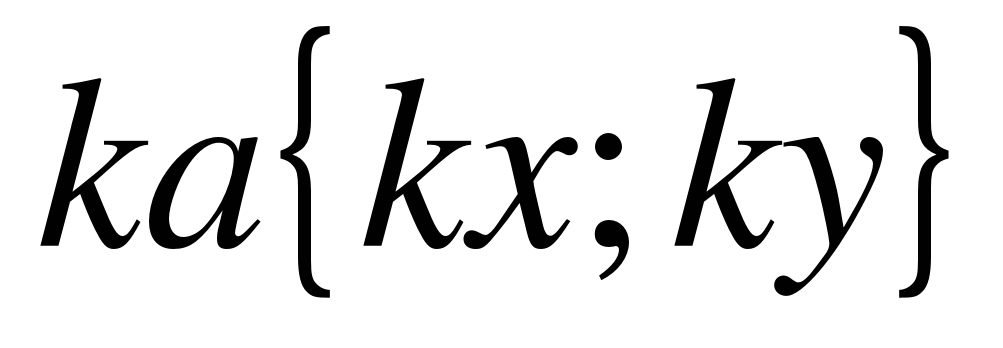 . Самостоятельно доказать с последующей проверкой. . Самостоятельно доказать с последующей проверкой. Доказательство: 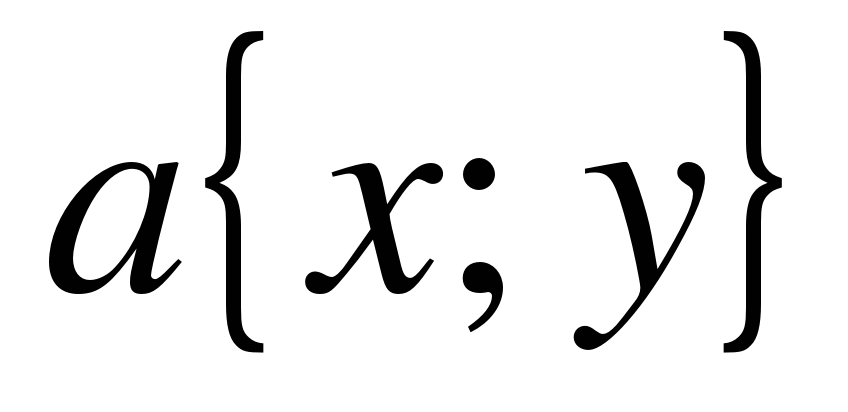 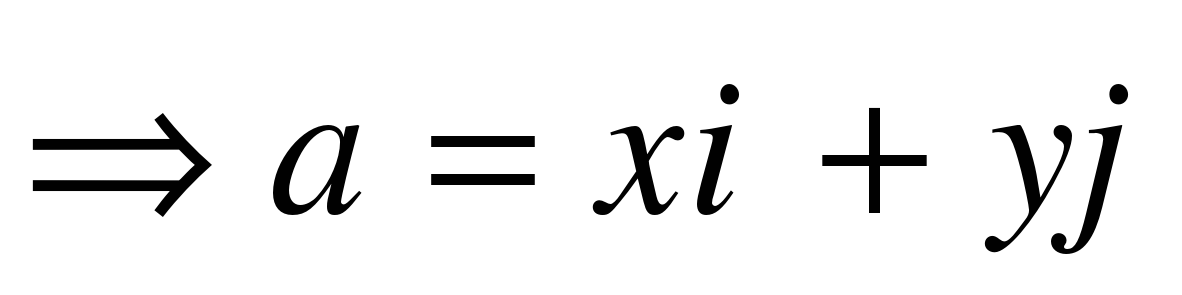 , ,
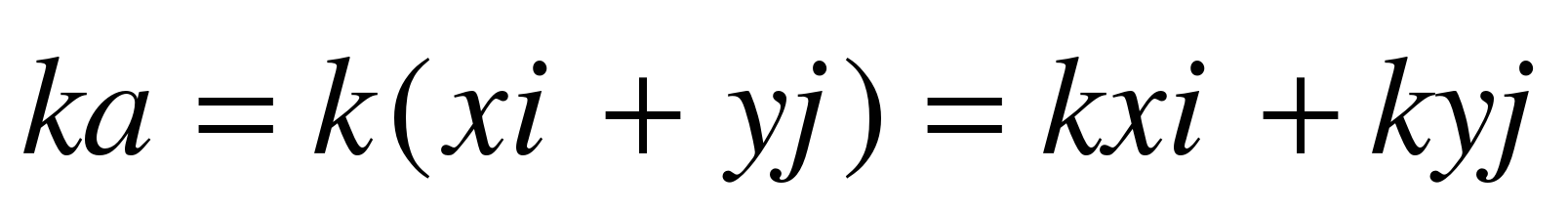 , следовательно , следовательно 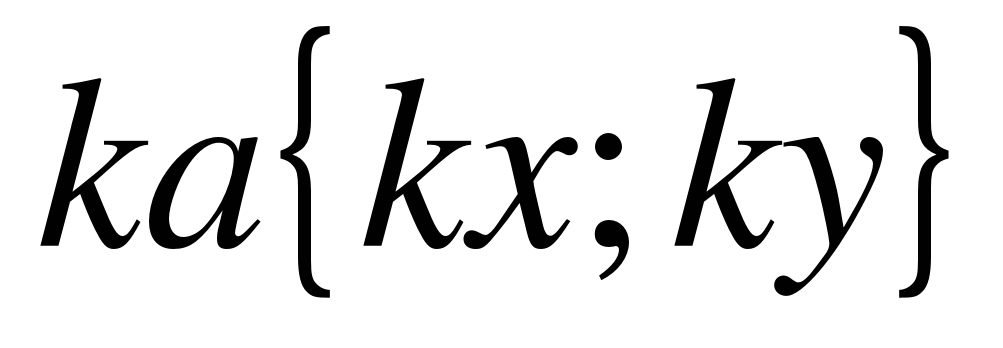 . .
Сформулируйте правило нахождения каждой координаты произведения вектора на число: Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Проговорите правило вслух; шепотом; про себя; друг другу. Ученик за доской №924 (- ) ) Вместе: № 926 (в)
| Отвечают на вопросы, выводят правила нахождения координат суммы, разности векторов, координат произведения вектора на число.
Решают типовые задания с проговариванием алгоритма вслух | Организует учащихся по исследованию проблемной ситуации.
Устанавливает осознанность восприятия. Первичное обобщение. |
ПУУД: логические решение проблемы, построение логической цепи рассуждений, доказательство, выдвижение гипотез и их обоснование. КУУД: инициативное сотрудничество в поиске и выборе информации
РУУД: контроль, оценка, коррекция. ПУУД: общеучебные – умение осознанно и произвольно строить речевое высказывание, рефлексия способов и условий действия.
|
| 6. Физминутка | Один из учеников проводит физминутку. Тихо сели, вновь за дело. | Выполняют действия, ориентируясь на показ движений учителем. | Организация физминутки | РУУД: осуществляют пошаговый контроль своих действий, ориентируясь на показ движений учителем |
| 7. Домашнее задание | Учебник: п.87(пересказ); Вопросы 8 стр 249; №922 ( б), № 923 (б), №924 (для -3 ), № 926 (б, г) ), № 926 (б, г)
| Записывают домашнее задание, задают вопросы, если есть. | Поясняет домашнее задание | РУУД: планирование деятельности. |
| 7. Рефлексия деятельности (итог урока) + Самостоятельная работа (с самопроверкой по эталону) | Вот и кончился урок. Подведём теперь итог. Выставить оценки учащимся, работающим у доски и учащимся, активно работавшим в течение всего урока. Какую цель мы сегодня перед собой ставили?
А сейчас проведем небольшую самостоятельную работу. Оценка «5» выставляется, если все верно выполнено; «4» - три вычислительная ошибка, ход работы верен; «3» - два задание верно выполнено 1 вариант: Даны векторы  и и 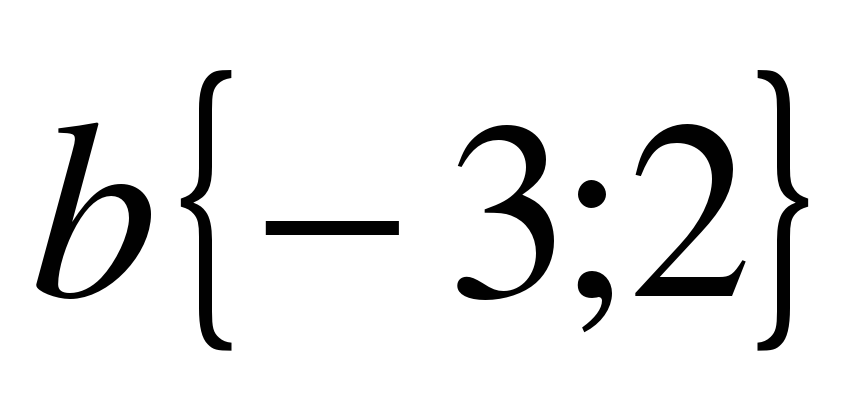 . Найдите координаты векторов: . Найдите координаты векторов: 1) 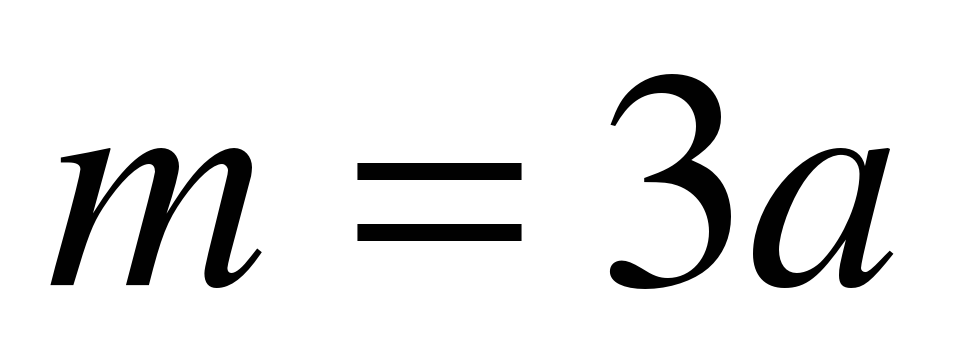 ; 2) ; 2) 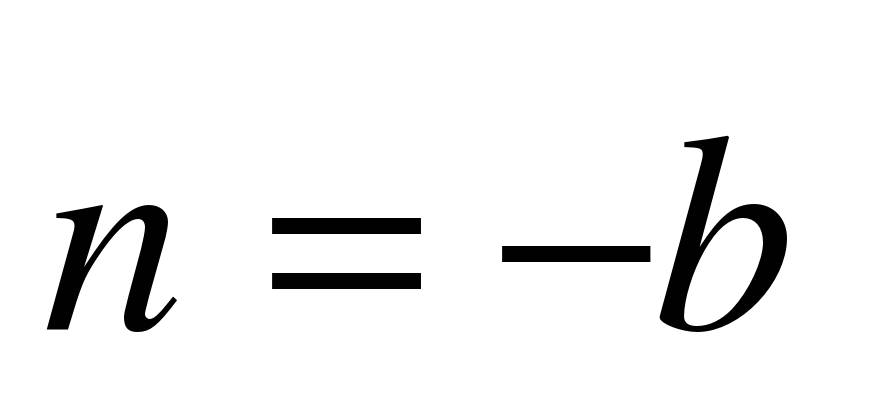 ; ; 3)  ; 4) ; 4) 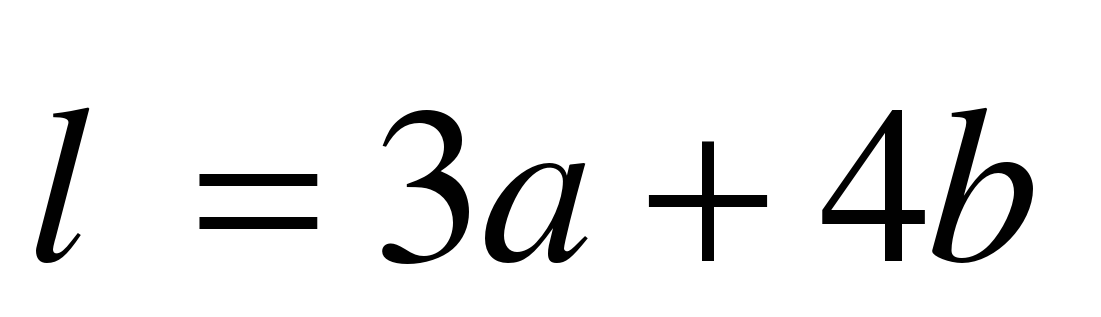 . . 2 вариант Даны векторы 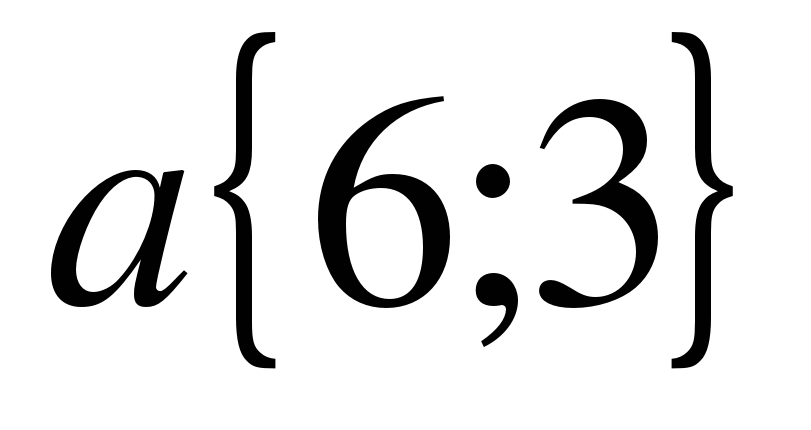 и и 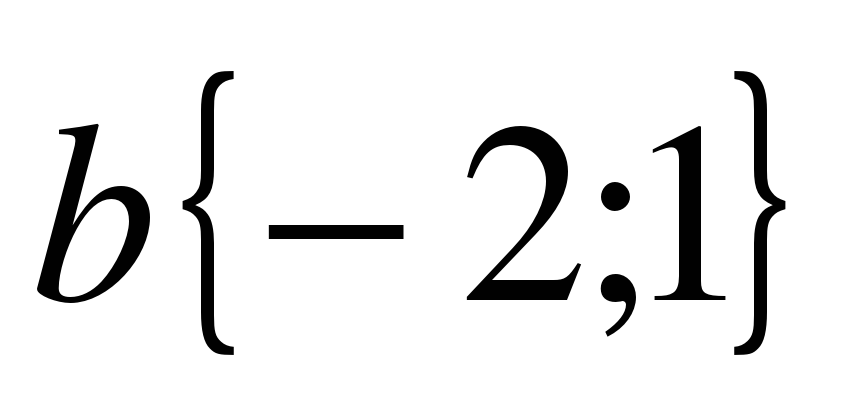 . Найдите координаты векторов: . Найдите координаты векторов: 1) 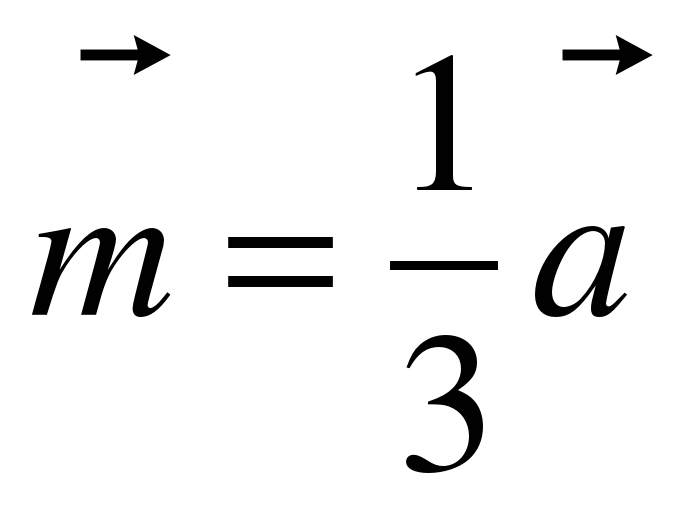 ; 2) ; 2) 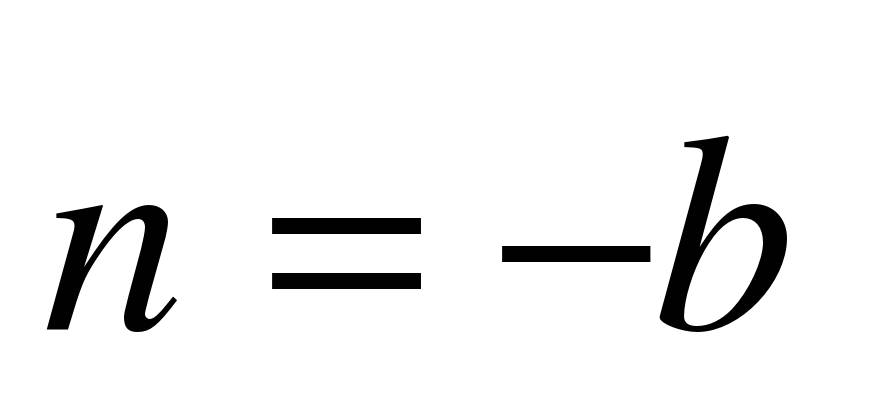 ; ; 3) 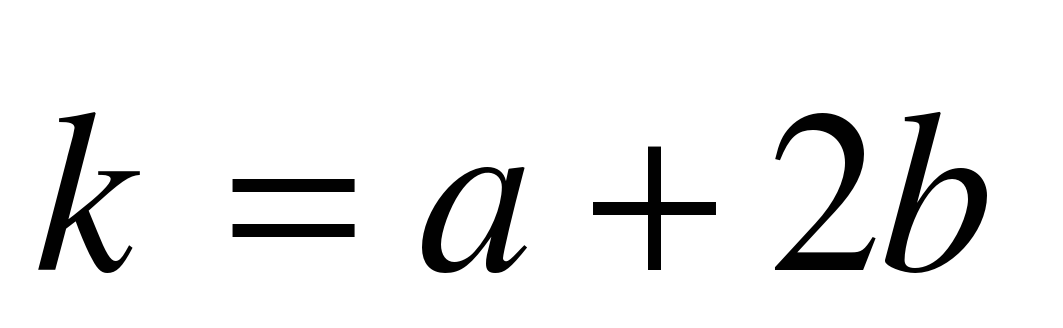 ; 4) ; 4) 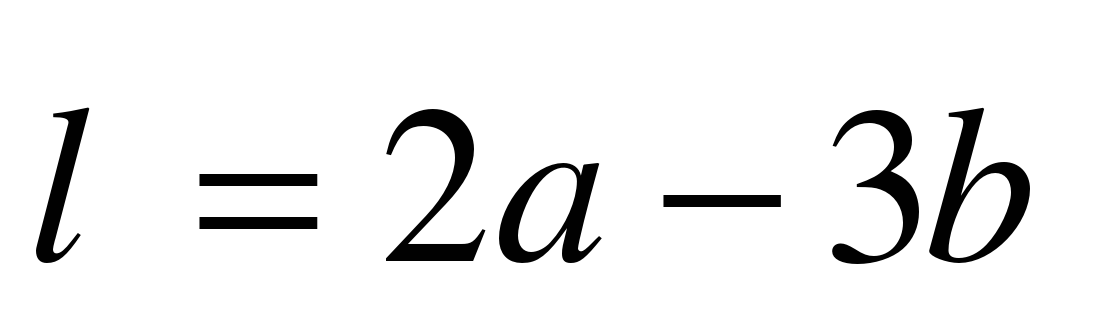 . . Ответы: 1 вариант: 1) 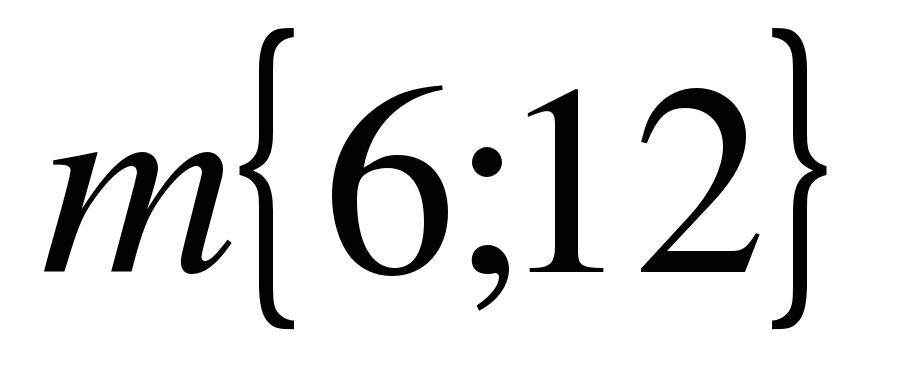 ; ; 2) 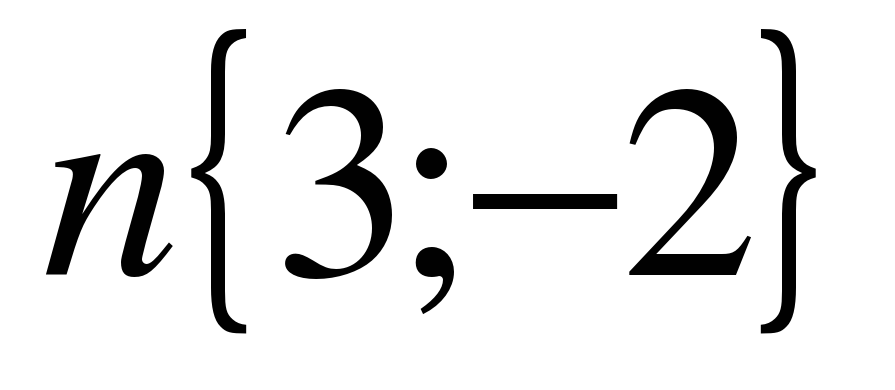 ; 3) ; 3)  ; 4) ; 4) 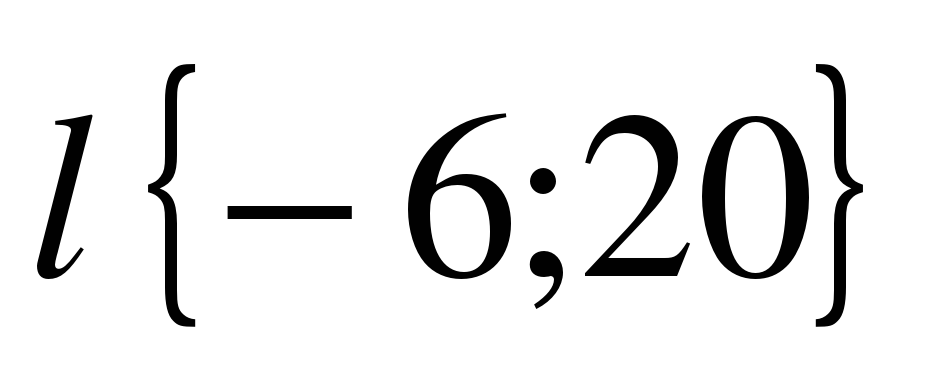 . . 2 вариант: 1) ; 2) ; 3) ; 4) Спасибо за урок! | Соотносят цель и результаты, ставят цель на следующий урок. Осуществляют самооценку собственной учебной деятельности. Приобретают навык рефлексии результатов деятельности.
Решают самостоятельную работу. Осуществляют самопроверку, пошагово сравнивая с эталоном | Организует рефлексию
Организует деятельность по применению новых знаний | КУУД: умение с достаточной полнотой и точностью выражать свои мысли. .
РУУД: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению. Осознание качества и уровня усвоения. ЛУУД: готовности оценить свой учебный труд. |
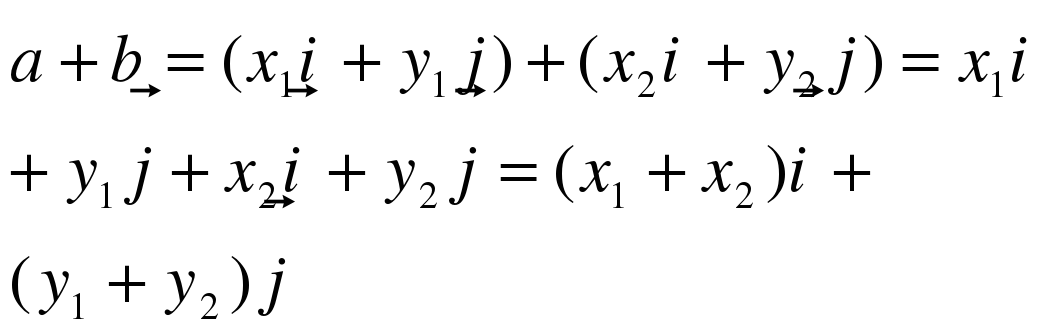 Вывод: Координаты суммы двух векторов:
Вывод: Координаты суммы двух векторов:  Вывод: Координаты разности двух векторов:
Вывод: Координаты разности двух векторов: 















