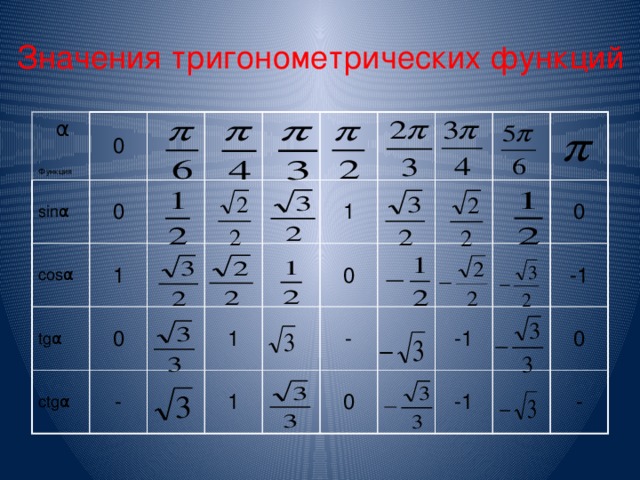
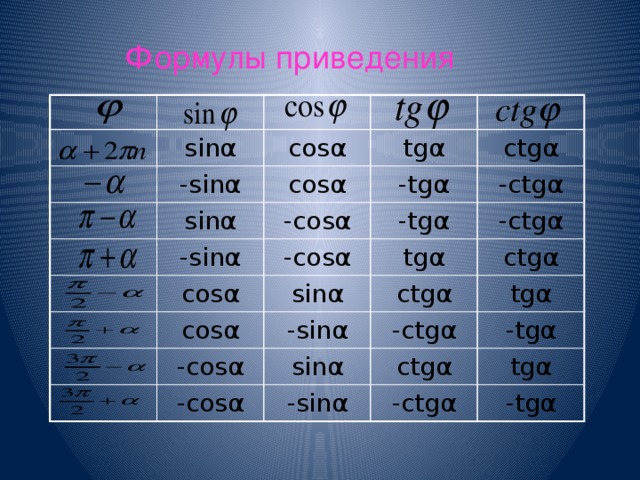
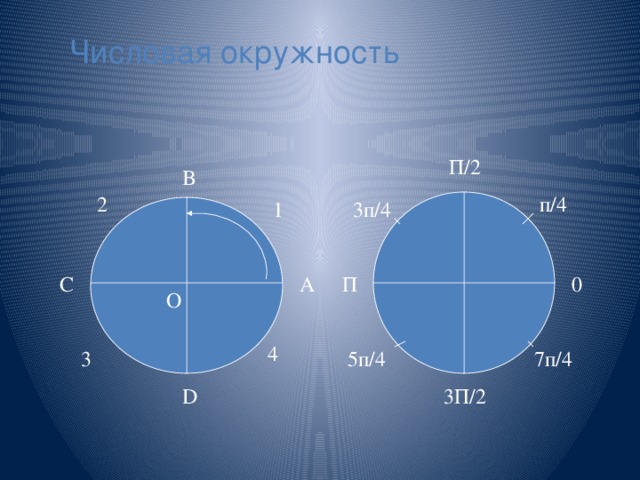
СТРУКТУРА ШКОЛЬНОГО КУРСА ТРИГОНОМЕТРИИ
История тригонометрии как науки
Тригонометрия, как и любая научная дисциплина, возникла из потребностей практической деятельности человека. Различные задачи астрономии, мореплавания, землемерия, архитектуры привели к необходимости разработки способа вычисления элементов геометрических фигур по известным значениям других их элементов, найденных путем непосредственных измерений. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: 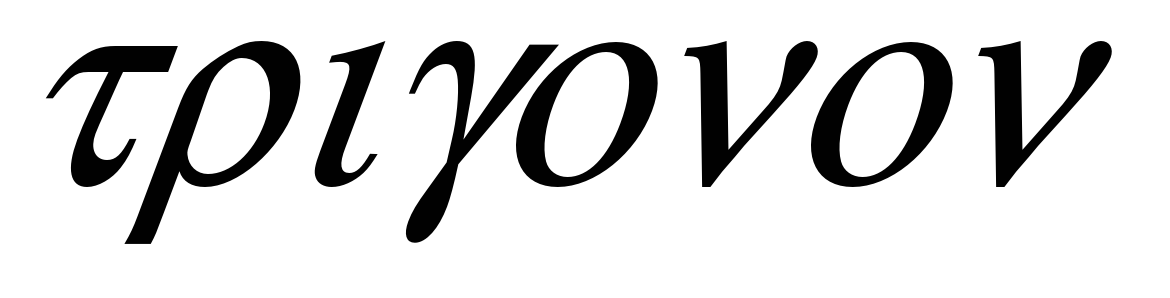 (тригонон) — треугольник,
(тригонон) — треугольник,  (метрейн) — измерение.
(метрейн) — измерение.
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии. Постепенно в геометрии и астрономии установились понятия синуса, косинуса и тангенса угла. По существу, ими оперировали еще древние математики, рассматривая отношение отрезков в треугольниках и окружностях.
Накопившийся материал астрономических наблюдений потребовал математической обработки. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во II в. до н.э. Гиппарх является автором первых тригонометрических таблиц. Эти таблицы до нас не дошли, но они вошли (в усовершенствованном виде) в сочинение «Великое построение» (Альмагест) знаменитого александрийского астронома Клавдия Птолемея, жившего во второй половине II в. н.э. В этих таблицах, в течение многих веков служивших средством для решения треугольников, давались значения хорд окружности для различных значений соответствующего центрального угла. Единицей измерения хорд служила 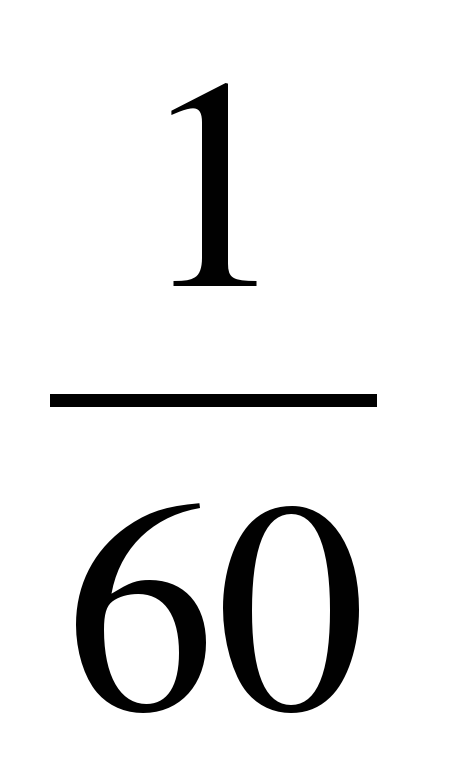 часть радиуса.
часть радиуса.
Эти таблицы, говоря современным языком, являются таблицами значений удвоенного синуса половины соответствующего центрального угла. В них были даны значения хорд для всех углов (через каждые полградуса) от 0° до 180°. Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в самостоятельную науку, а считалась частью астрономии.
Важный вклад в развитие тригонометрии был внесен индийской математикой в период V-ХП вв. н.э. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», что буквально означало «половина тетивы лука». Индийцы составили таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 0° до 90° (через каждые 3°45'). Эти таблицы были точнее таблиц Птолемея. Об их высокой точности говорит тот факт, что для синуса и косинуса 3°45' были вычислены значе-
ния  и
и  , отличающиеся от истинных менее чем на 10 -8.
, отличающиеся от истинных менее чем на 10 -8.
Индийским математикам были известны соотношения, которые в современных обозначениях пишутся так:
sin2 x + cos2 x = 1; cos  = sin
= sin  (900 -
(900 -  )
)
В XI –ХIII вв. в трудах математиков Средней Азии, Закавказья, Ближнего Востока и Индии началось формирование тригонометрии как отдельной науки. И в дальнейшем потребности географии, геодезии, военного дела способствовали развитию тригонометрии как науки. Особенно усиленно тригонометрия развивалась в средние века, в первую очередь на юго-востоке: в Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насирад-Дин ат-Туси, ал-Каши, ал-Бируни), в Арабии (Ахмад, ибн-Абдаллах, ал-Баттани). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насирад-Дину Мухаммаду ат-Туси (1201-1274), написавшему «Трактат о полном четырехугольнике». Работы ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела математики. Однако в их трудах еще не было необходимой символики, и поэтому развитие тригонометрии происходило медленно.
С XV в. и в Европе появляются работы, посвященные вопросам тригонометрии. Немецкий ученый Иоган Мюллер (1436-1476), известный в науке под именем Региомонтан, издал труд «Пять книг о треугольниках всех видов», сыгравший важную роль в развитии тригонометрии. В нем дано систематическое изложение тригонометрии как самостоятельной научной дисциплины. Региомонтан составил таблицы синусов с точностью уже до 10-7. В его таблицах радиус круга принимался за 107вместо числа кратного 60, то есть, по сути, был совершен переход от шестидесятеричной системы измерения к десятичной. В 1595 г. появился труд Варфоломея Питискуса «Тригонометрия, или Краткий обзорный трактат о решении треугольников».
В ХV - ХVII в. в Европе было составлено и издано несколько тригонометрических таблиц. Над их составлением работали крупнейшие ученые: Н. Коперник (1473-1543), И. Кеплер (1571-1630), Ф. Виет (1540-1603) и др. В России первые тригонометрические таблицы были изданы в 1703 г. при участии Л.Ф. Магницкого.
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (1707-1783). Эйлер стал рассматривать значения тригонометрических функций как числа — величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи sin  , cos
, cos  , tg
, tg  , ctg
, ctg  . Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
. Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н.И. Лобачевского.
Современная точка зрения на тригонометрические функции как на функции числового аргумента во многом обусловлена развитием физики, механики, техники. Эти функции легли в основу математического аппарата, при помощи которого изучаются различные периодические процессы: колебательные движения, распространение волн, движения механизмов, колебание переменного электрического тока. Как показал Ж. Фурье (1768-1830), всякое периодическое движение с любой степенью точности можно представить в виде суммы простейших синусоидальных (гармонических) колебаний. Если в начале развития тригонометрии соотношение sin2 x + cos2 x = 1 лишь выражало зависимость между площадями квадратов, построенных на сторонах переменного прямоугольного треугольника с гипотенузой равной 1, то в последующем это соотношение стало отражать также сложение двух колебательных движений с происходящей при этом интерференцией.
Таким образом, на первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное и столь же важное значение имеет изучение свойств тригонометрических функций. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн.
В этот период даны обобщения многим терминам тригонометрии и, в частности, выведены соотношения для sin ( 1+
1+ 2.+ …+
2.+ …+  n), tg n
n), tg n , где n - натуральное число, и др. Функции sin x и cos x рассматриваются теперь как суммы степенных рядов:
, где n - натуральное число, и др. Функции sin x и cos x рассматриваются теперь как суммы степенных рядов:
sin x = x - 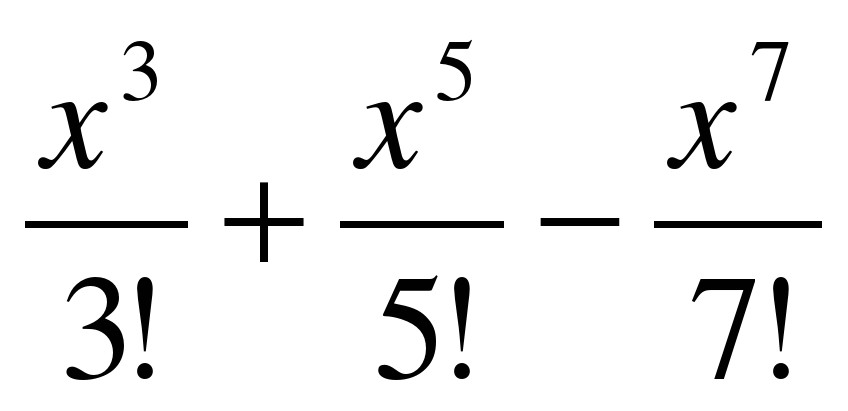 + …
+ …
cos x = 1 -  + …
+ …
Одновременно развивается учение о тригонометрических функциях комплексного переменного.