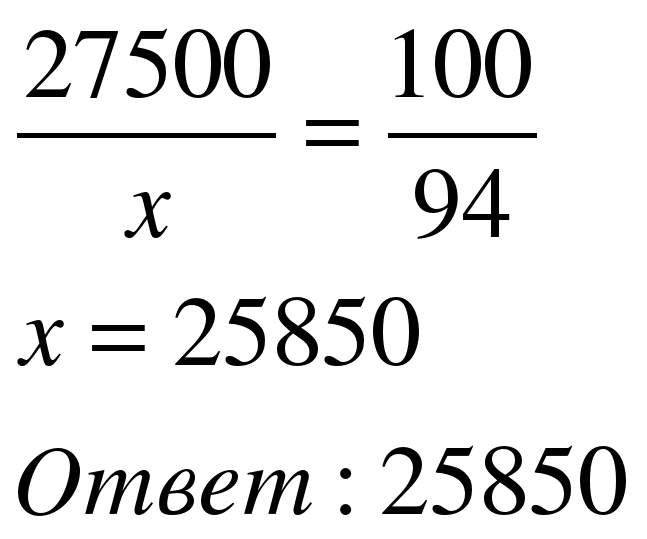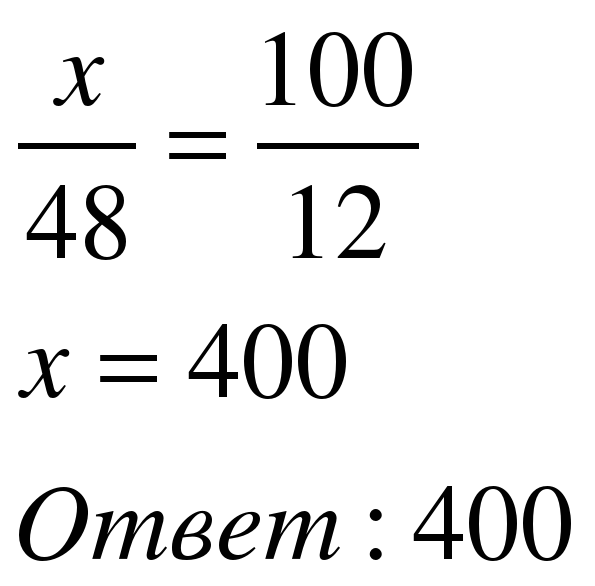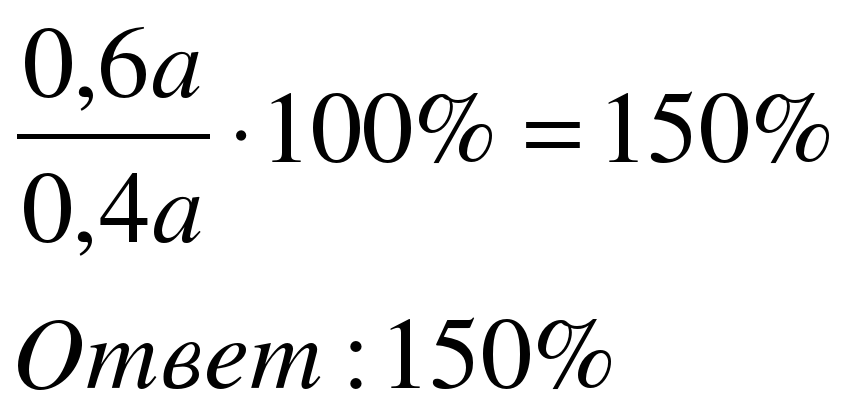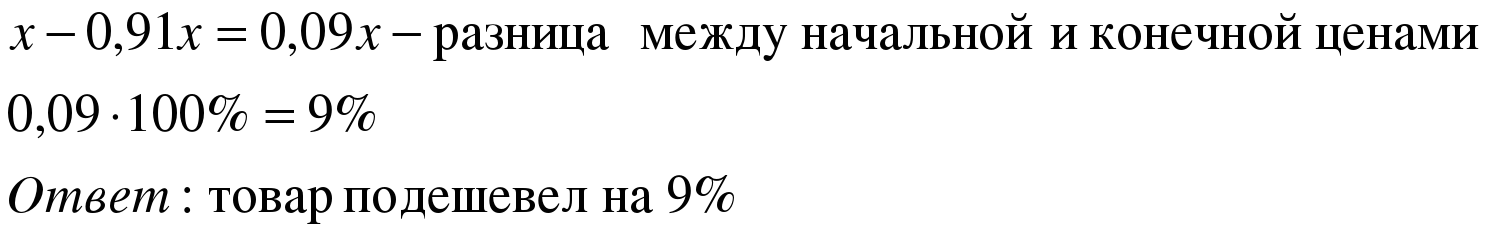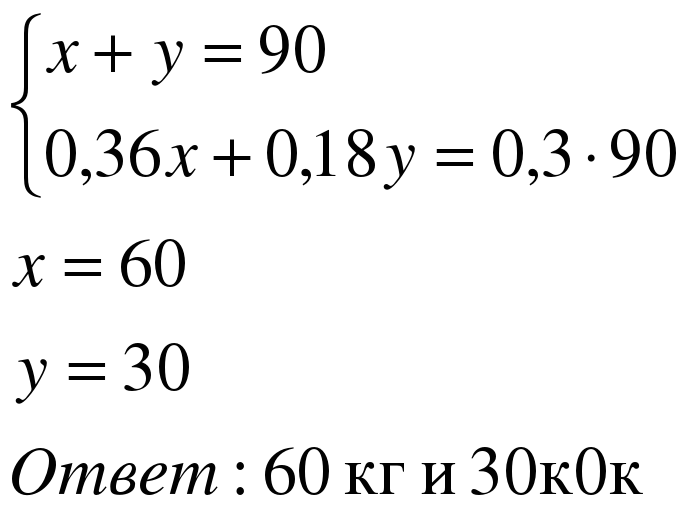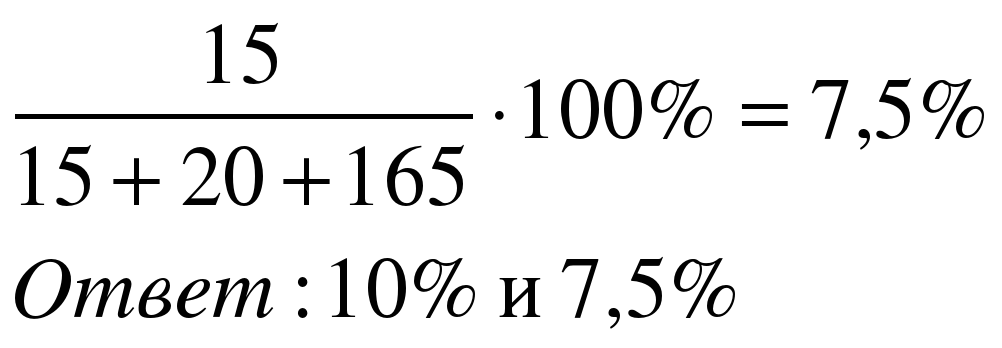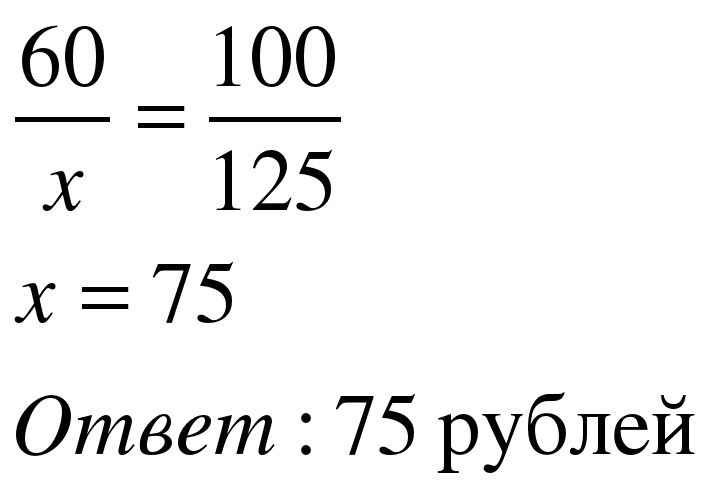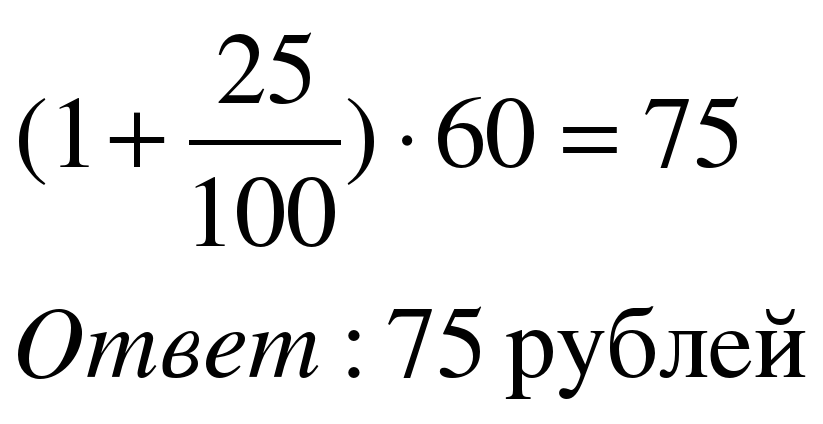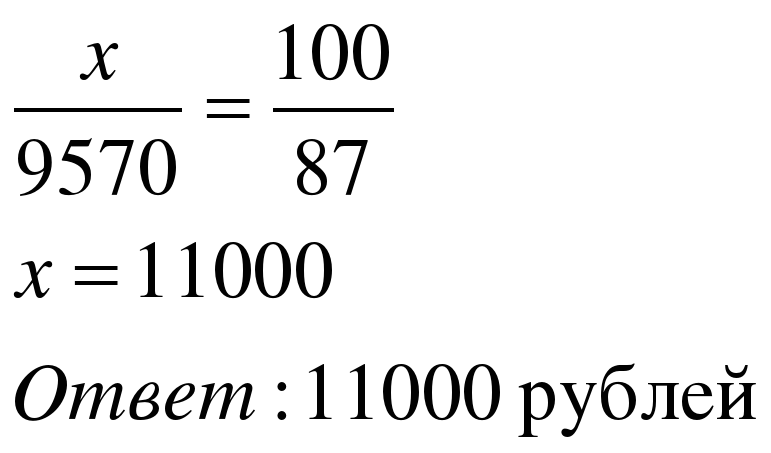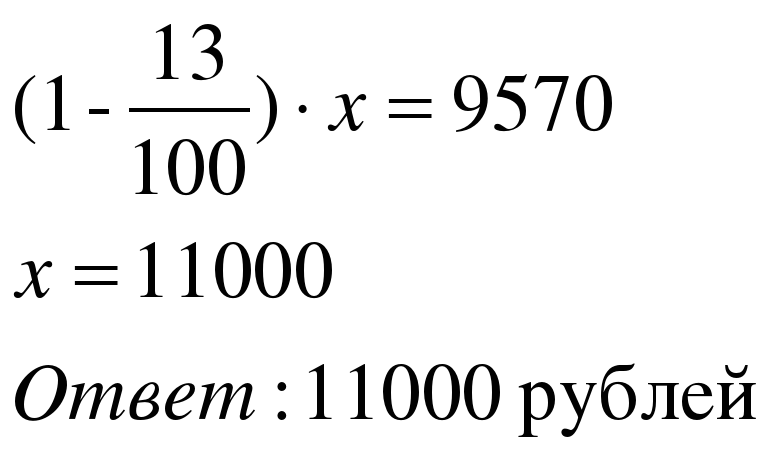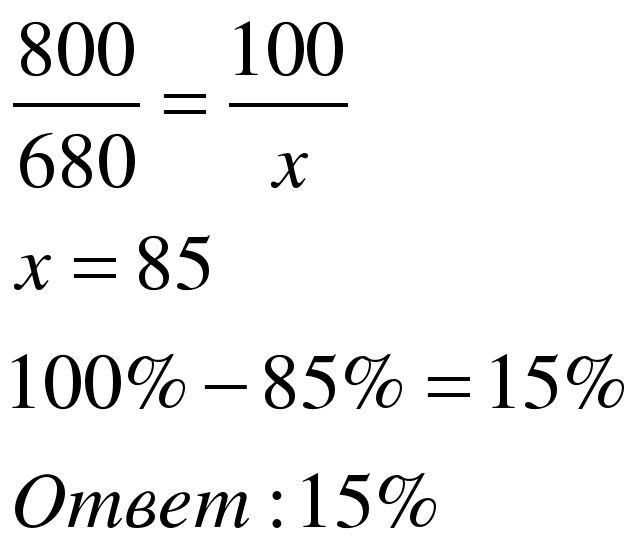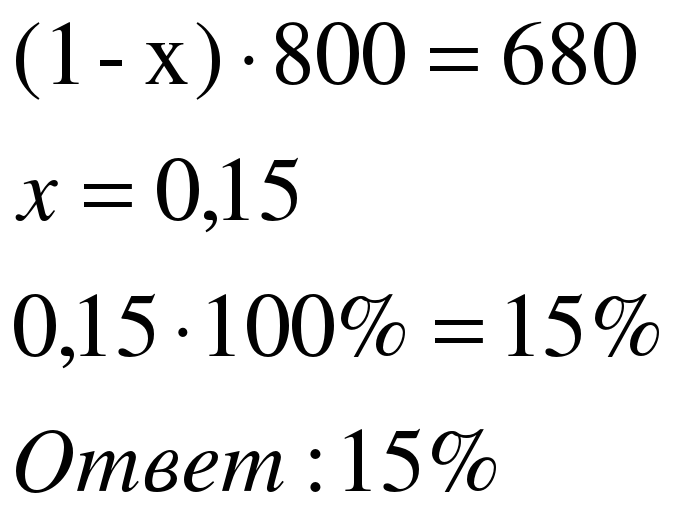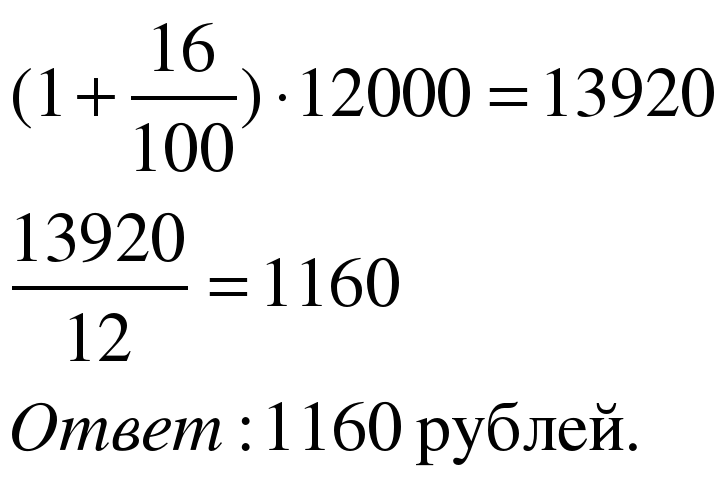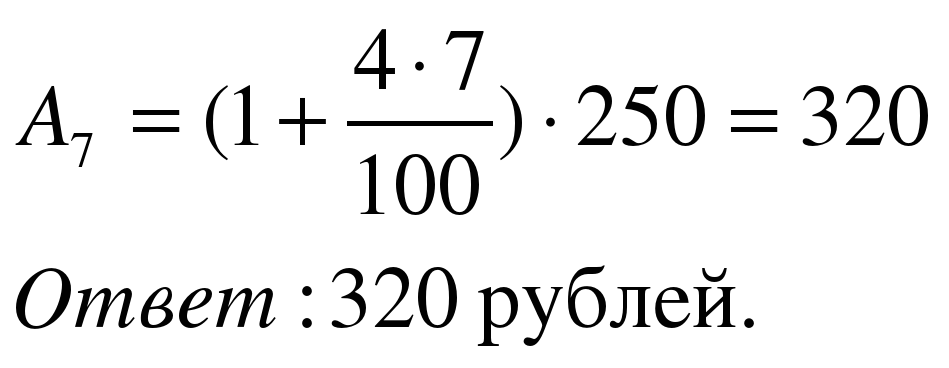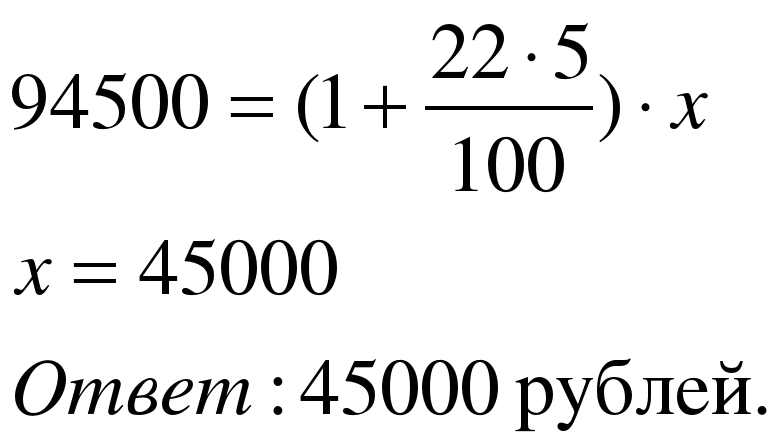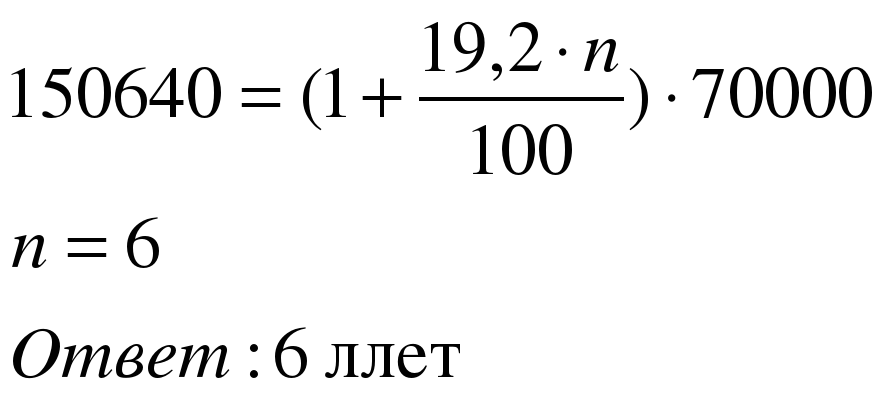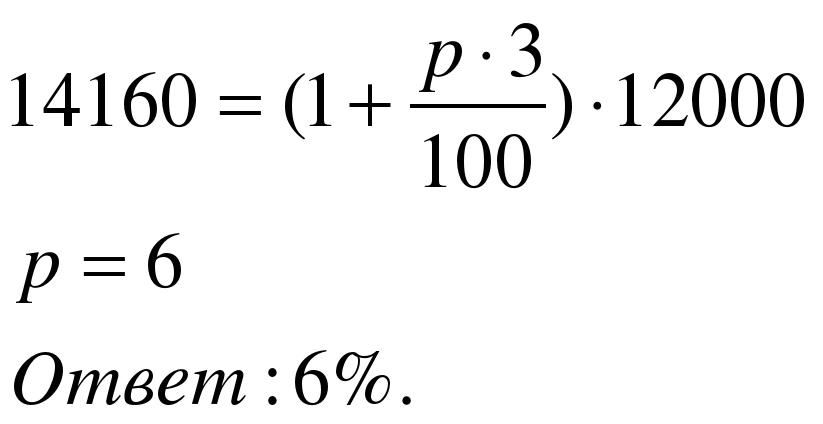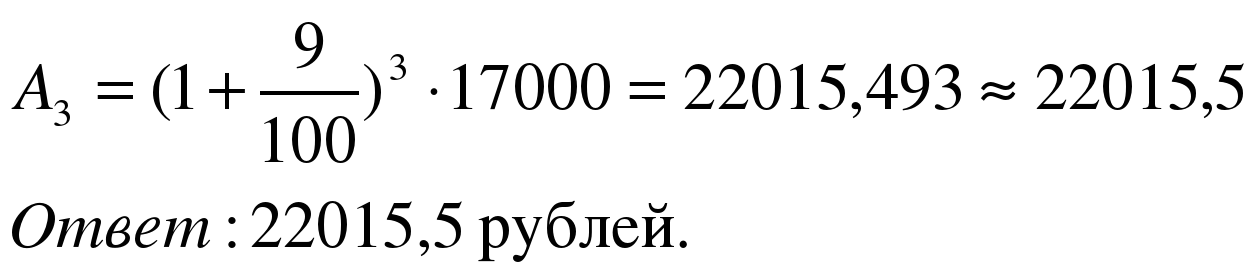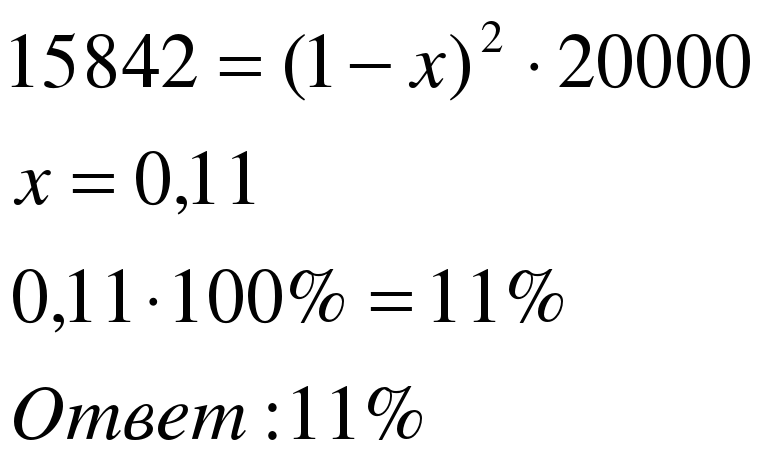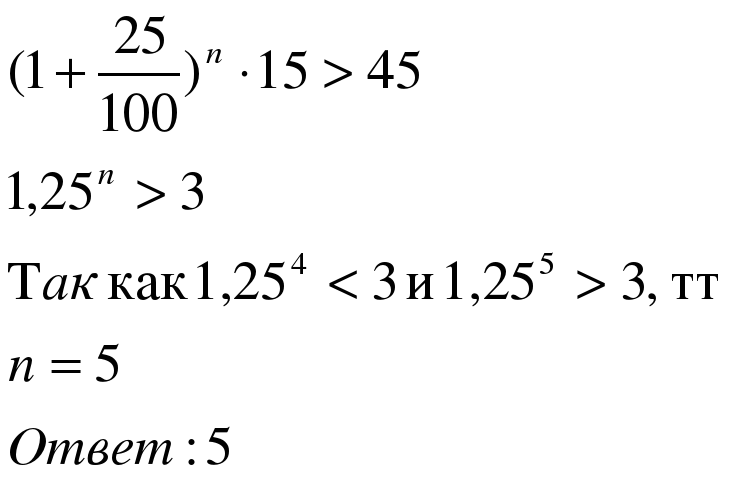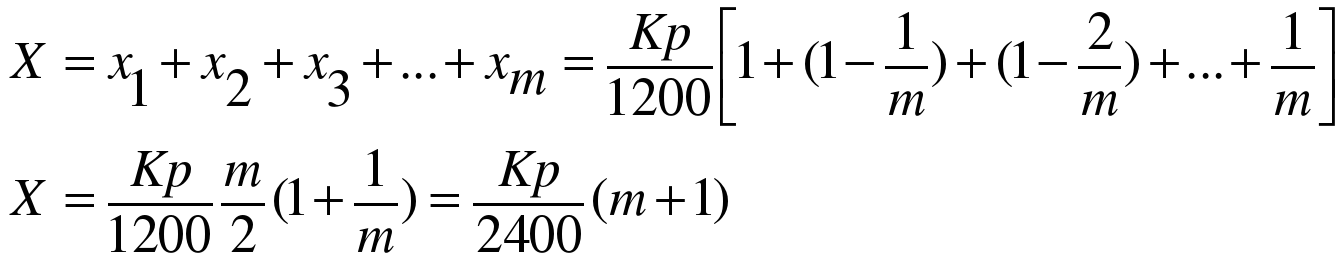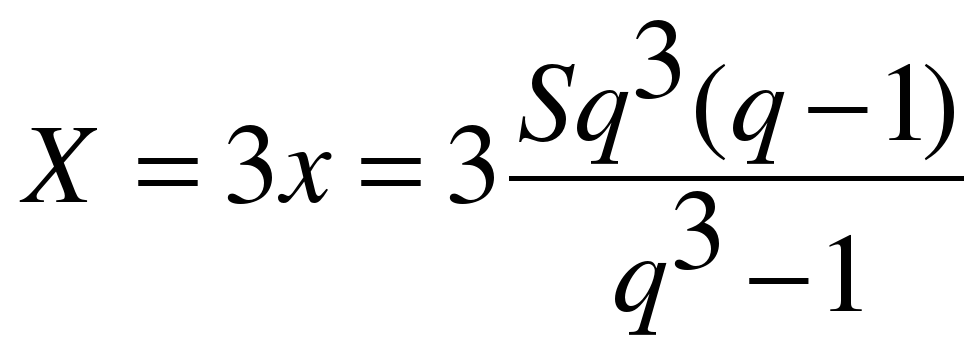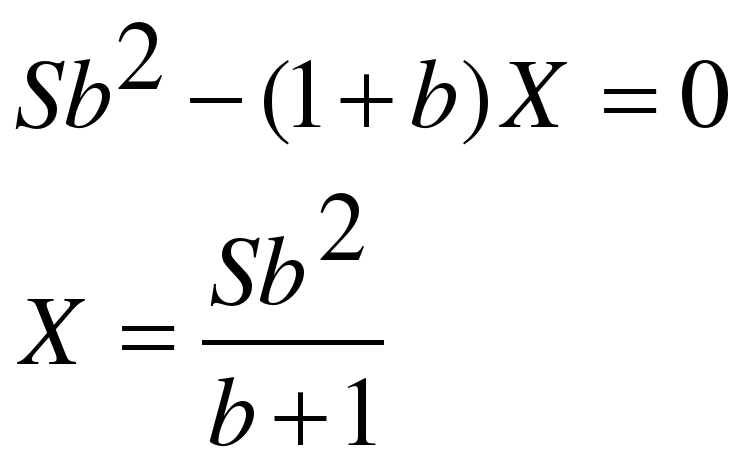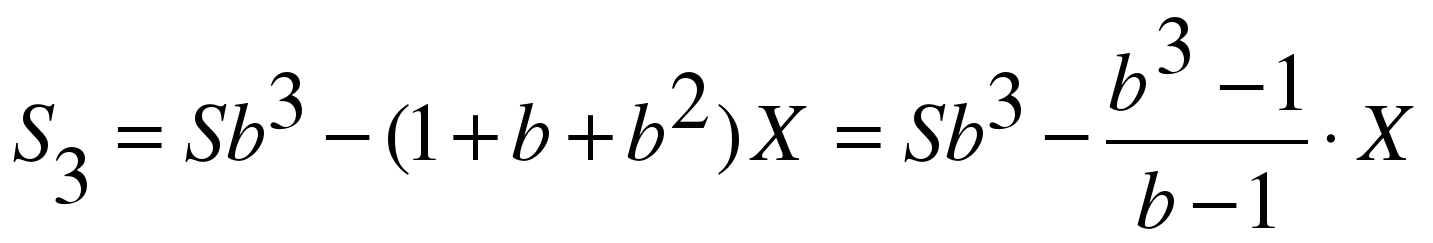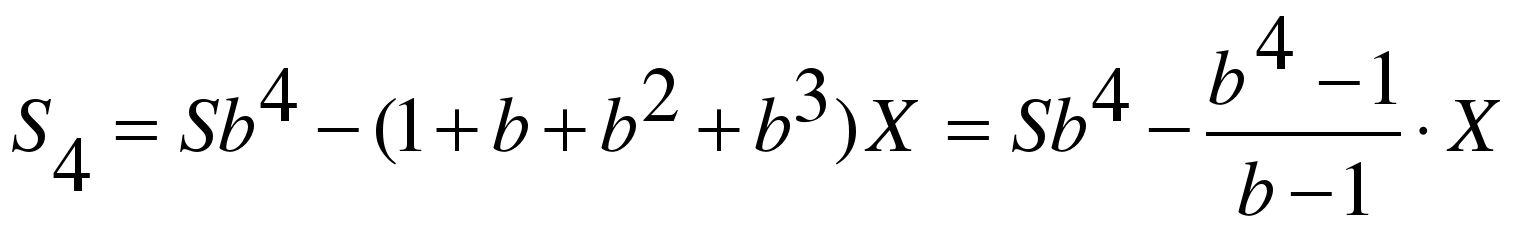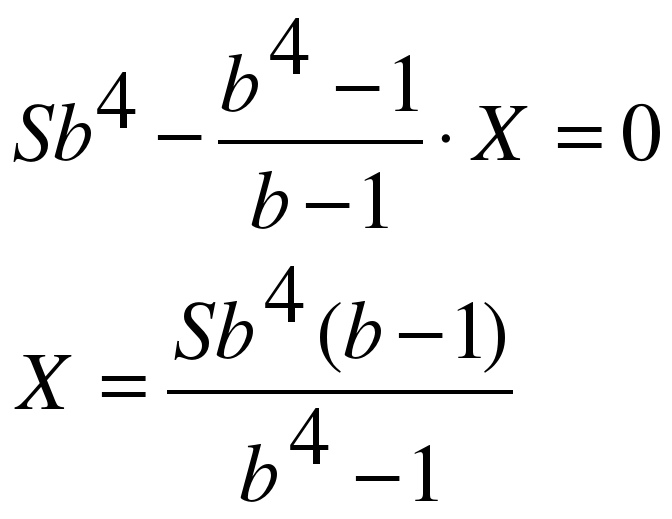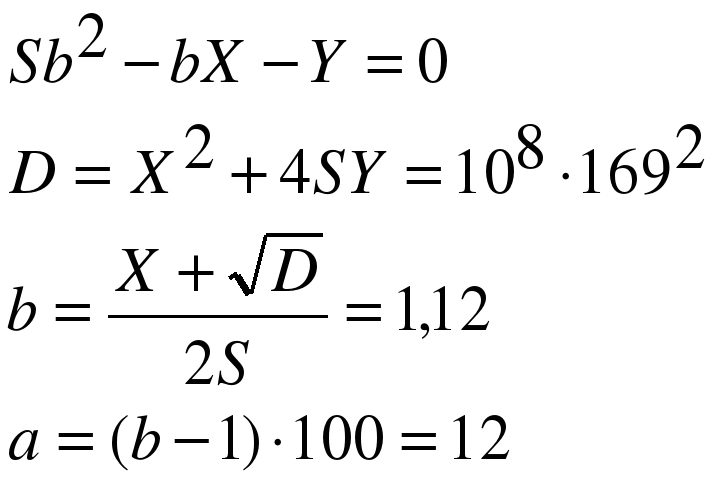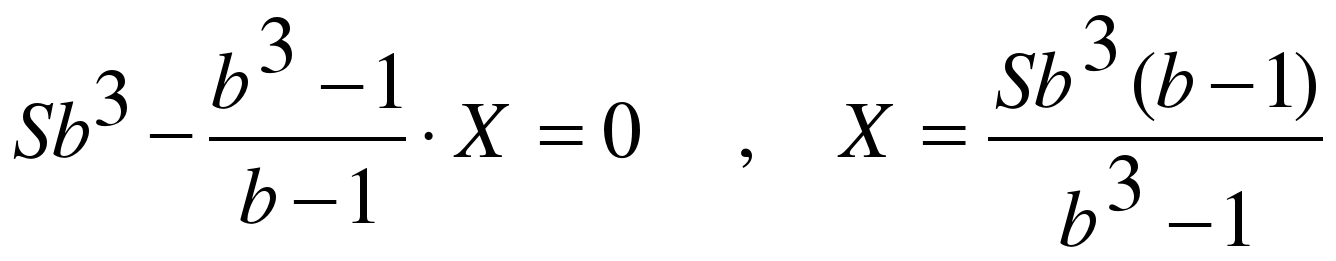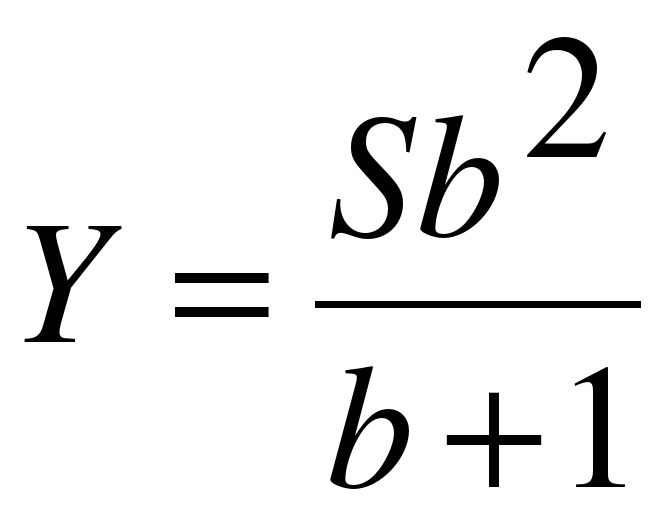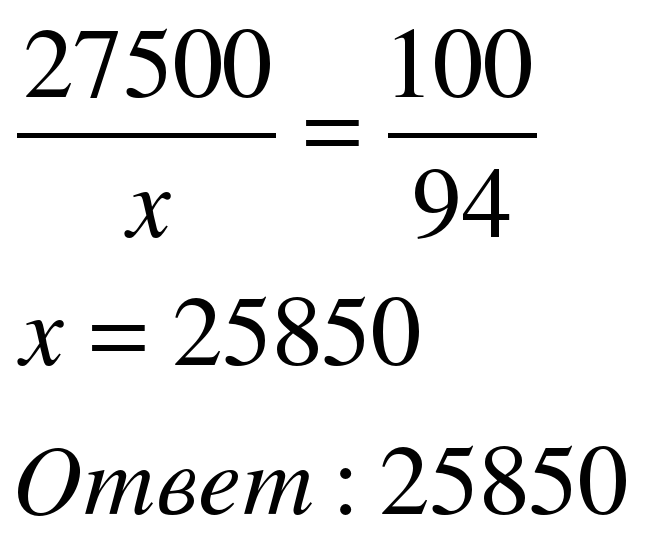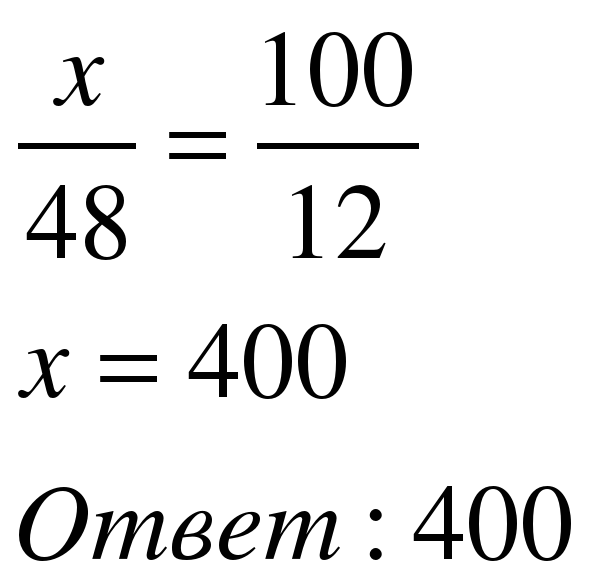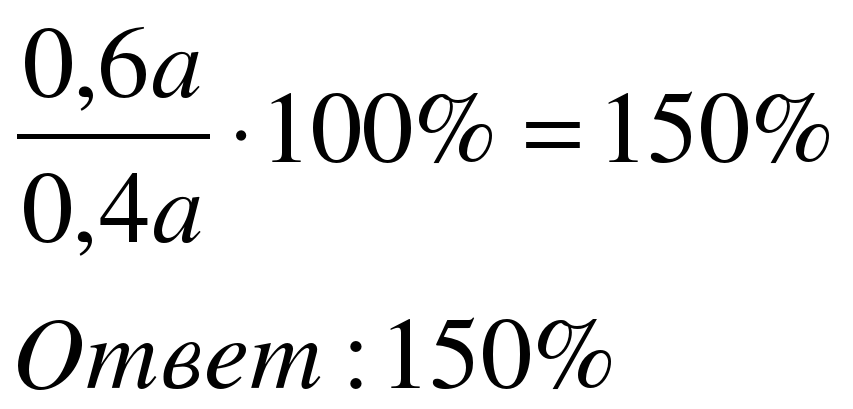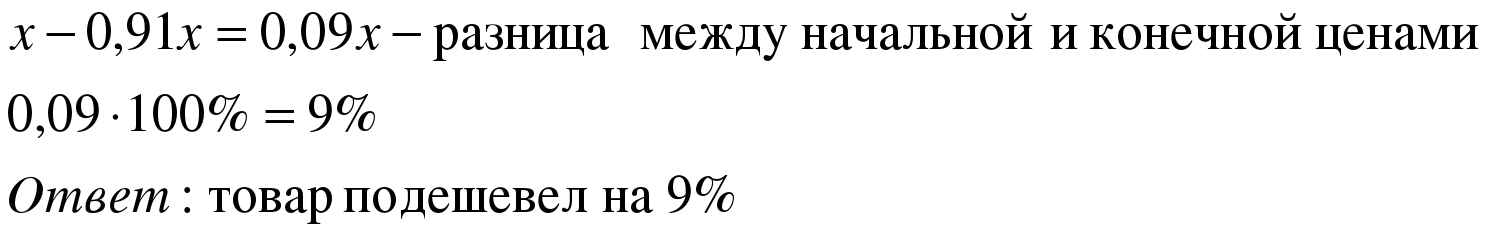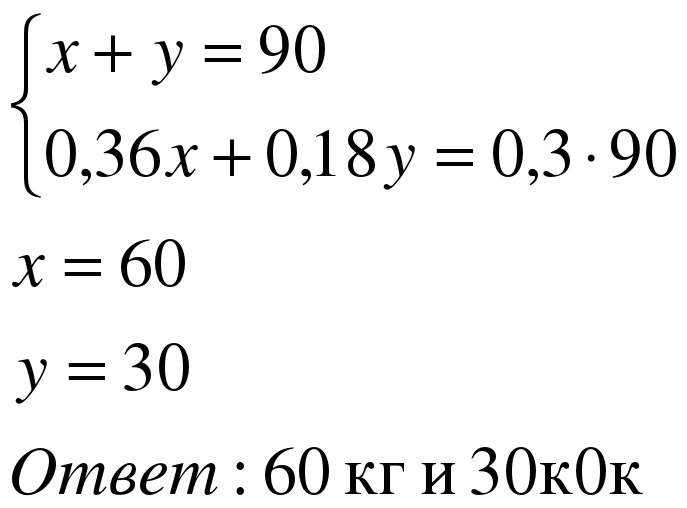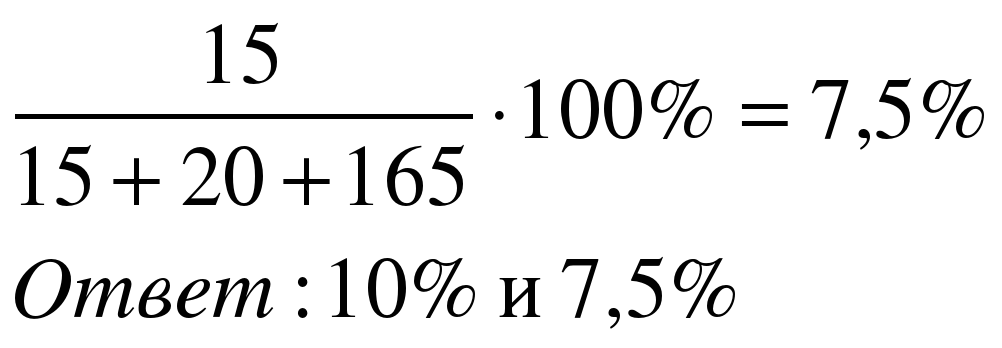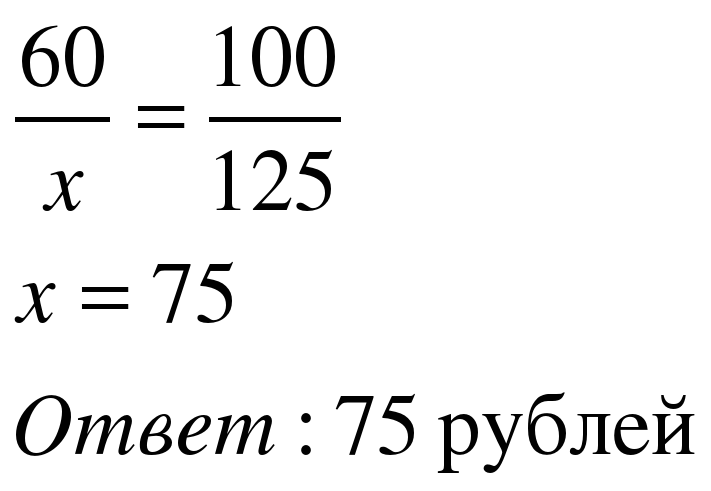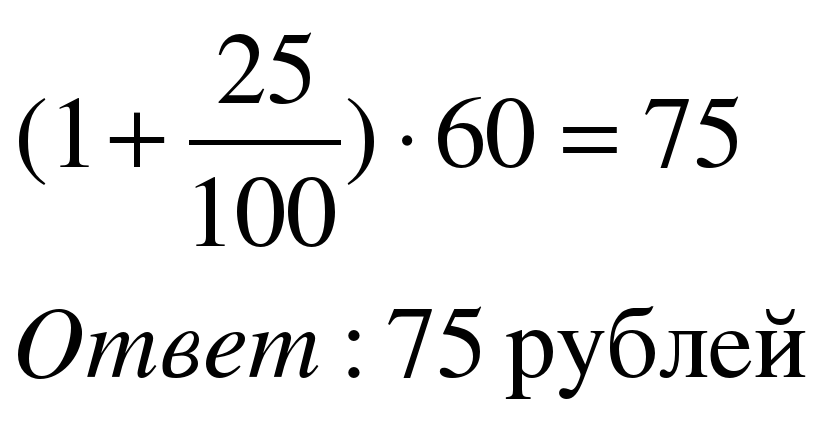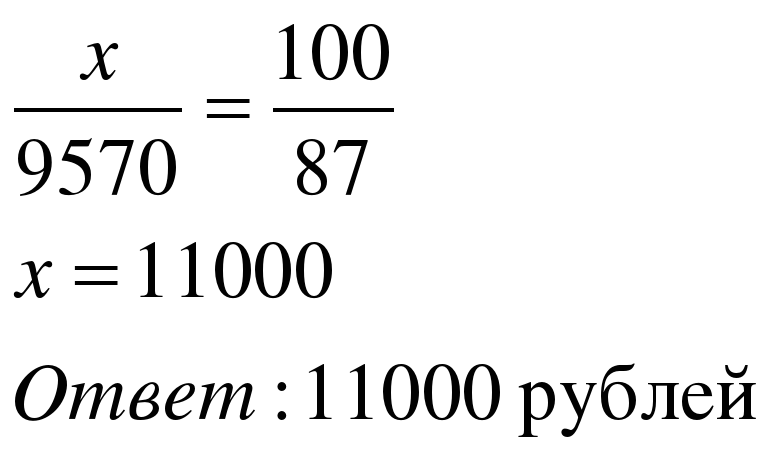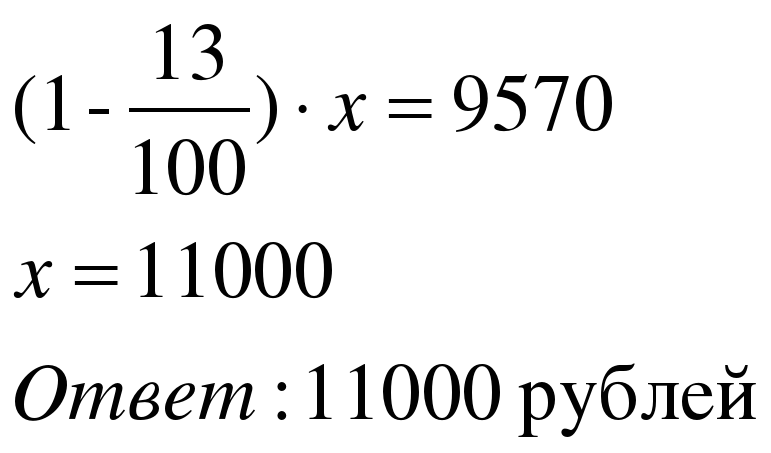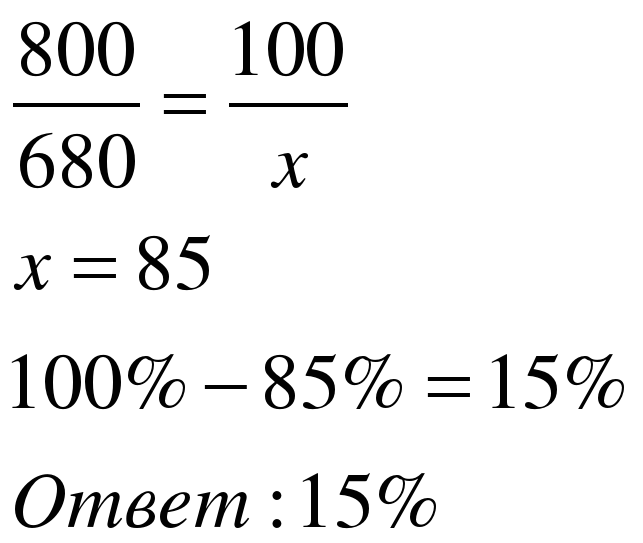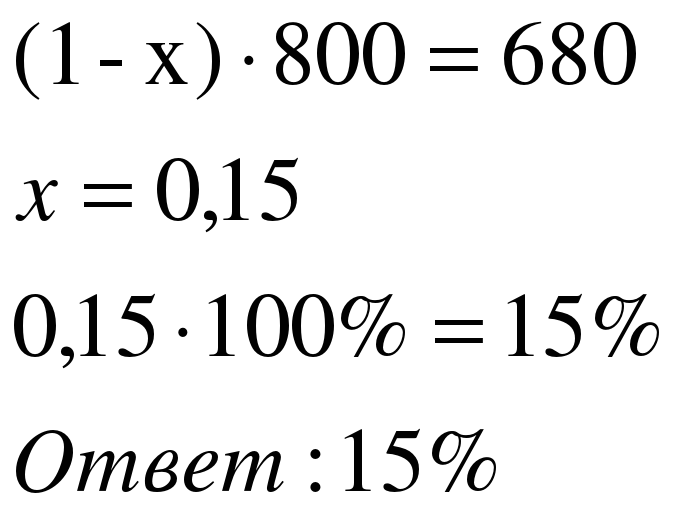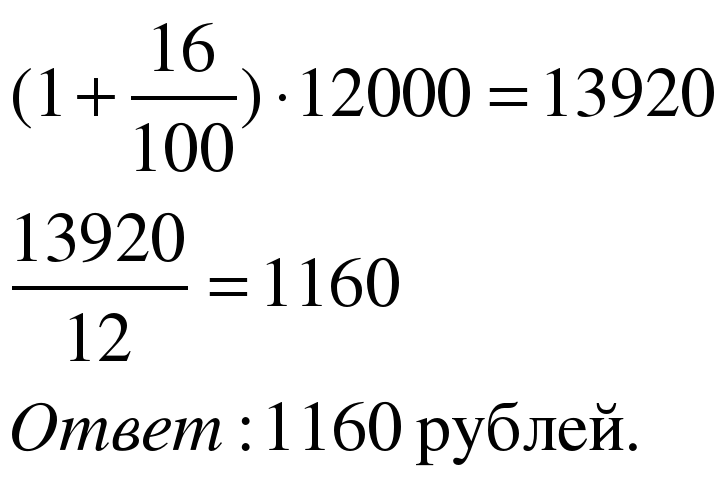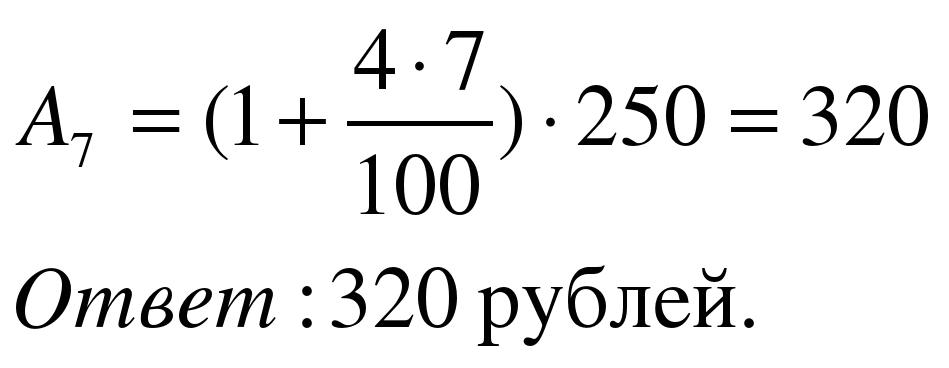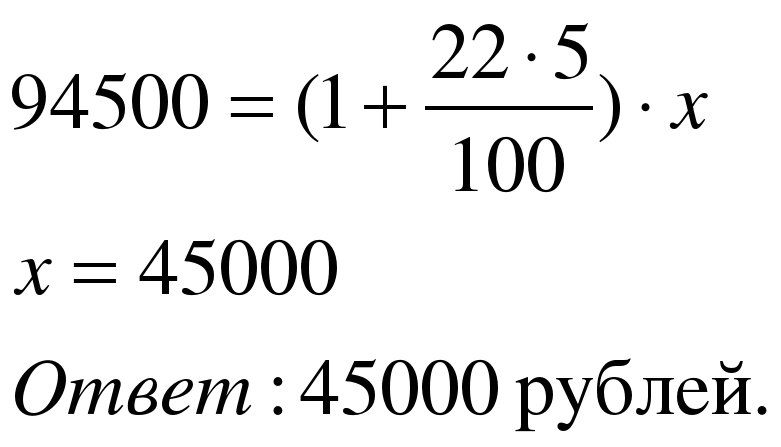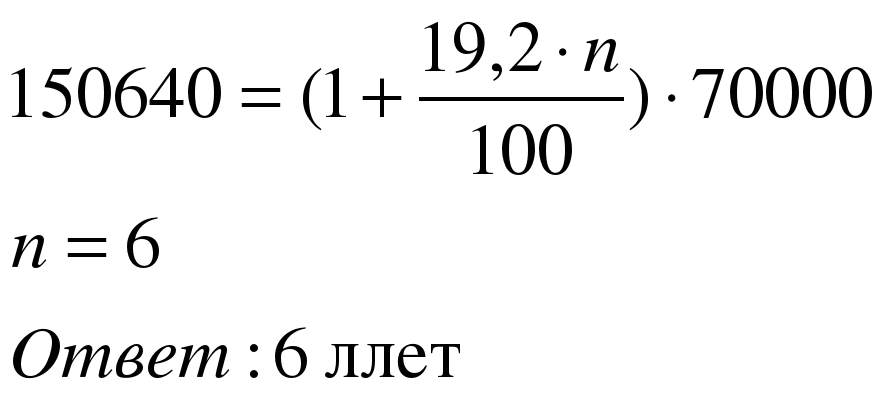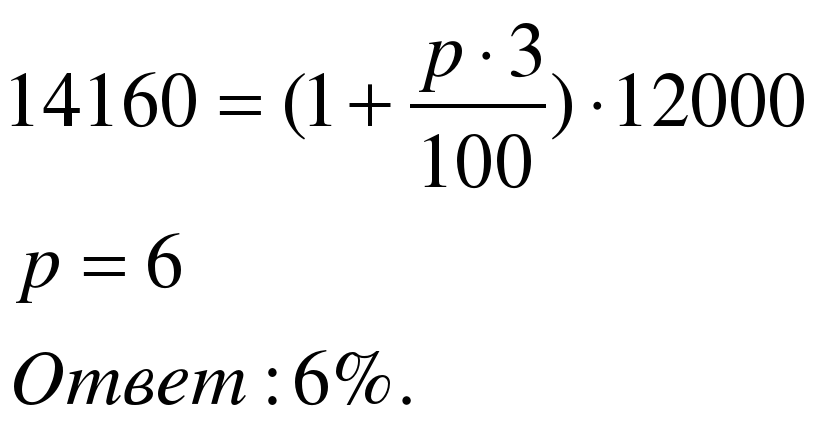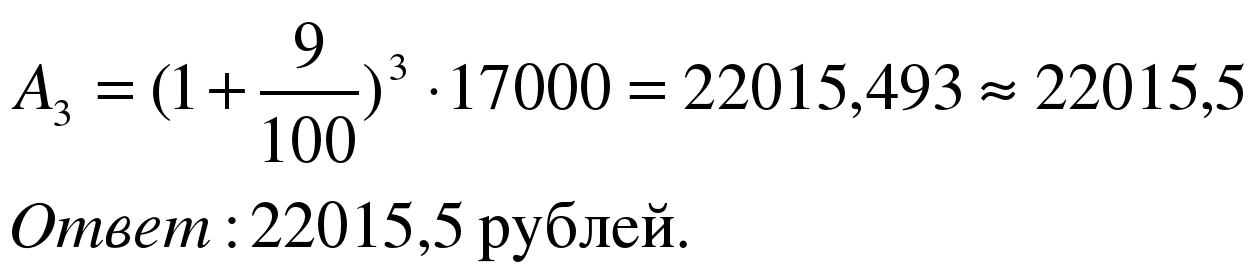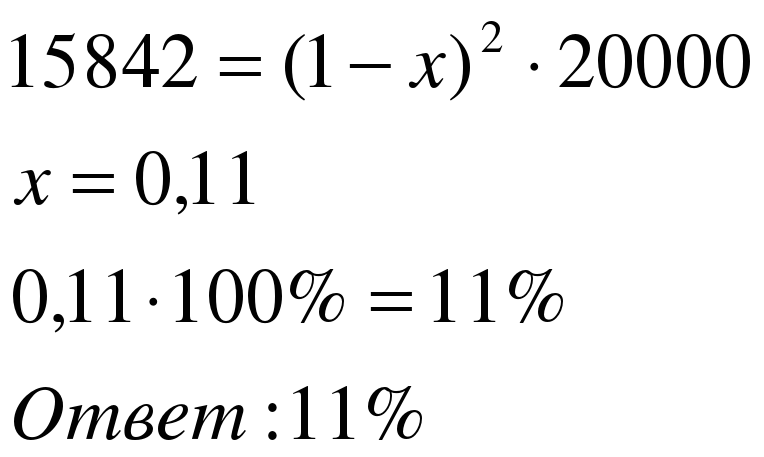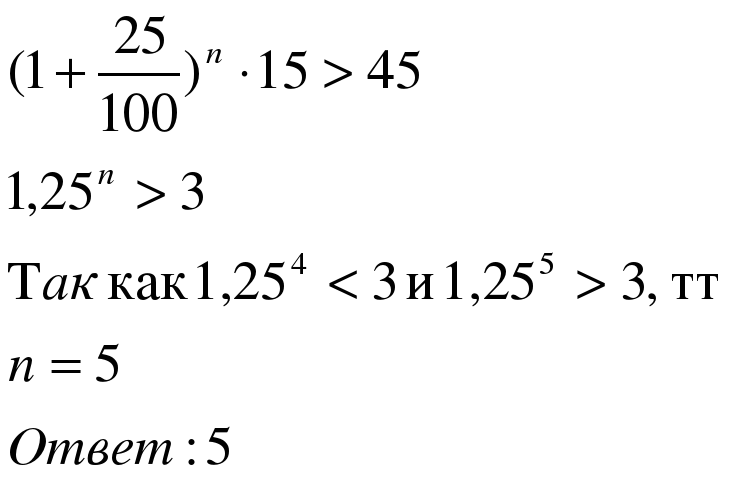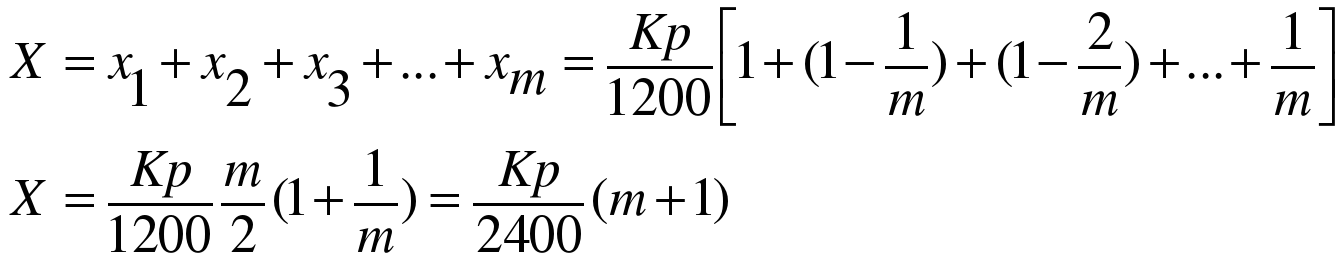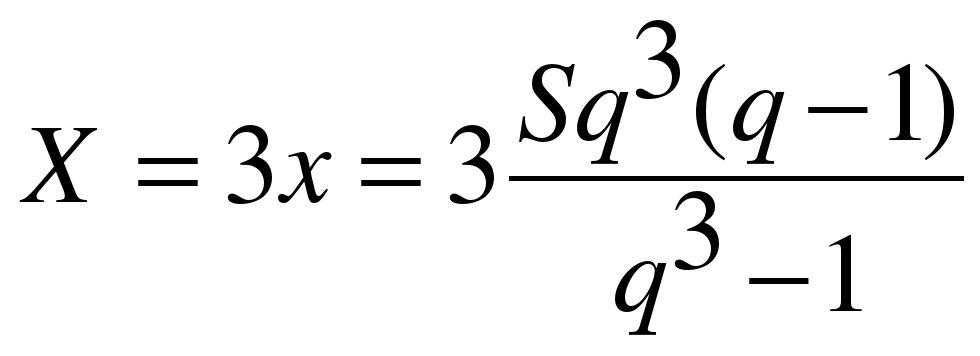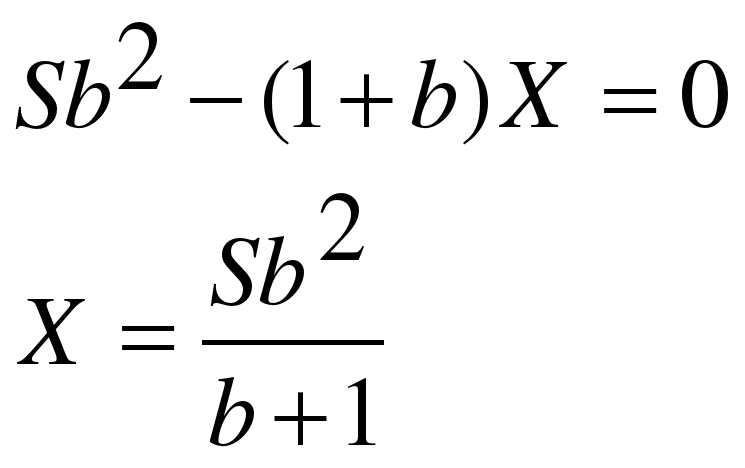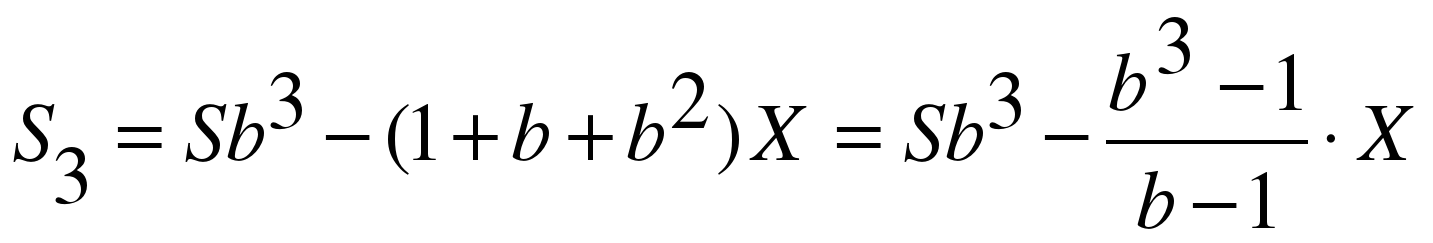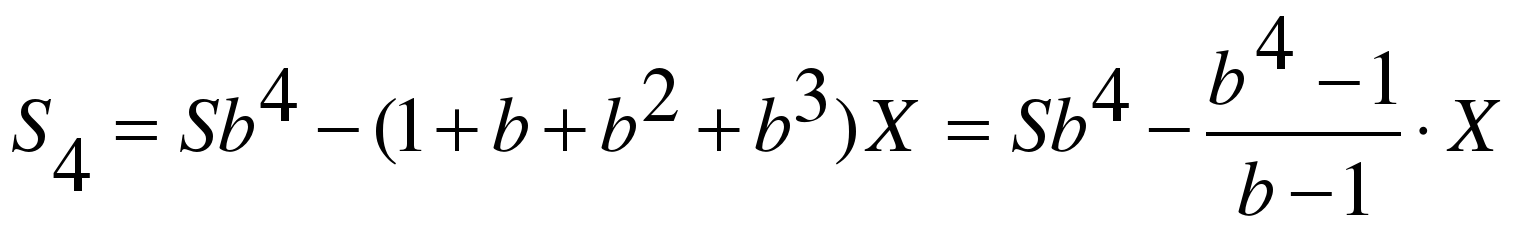С 2015 года вариант ЕГЭ по математике в новом формате содержит новое задание высокого уровня, представляющее собой практико ориентированную задачу. Использование подобных задач в варианте предполагает проверку умения учащихся обращаться с целыми числами, т.е. умения использовать при решении таких задач элементов теории делимости целых чисел, действий со степенями с натуральным показателем, знания и умения обращаться с процентами, сложными банковскими процентами и долями.
Прежде чем переходить к решению задач такого вида необходимо напомнить теоретический материал и рассмотреть подготовительные задачи.
СОДЕРЖАНИЕ
Занятие 1. «Простейшие задачи на проценты»
Занятие 2. «Решение задач на проценты»
Занятие 3. «Процентное изменение величины».
Занятие 4. «Формула простых процентов»
Занятие 5. «Формула сложных процентов»
Занятие 6. «Кредиты»
Занятие 1. «Простейшие задачи на проценты».
Теоретический аспект
Процент – сотая доля (часть) целого.
Пусть число а составляет к % от числа в. Алгебраически это можно записать так
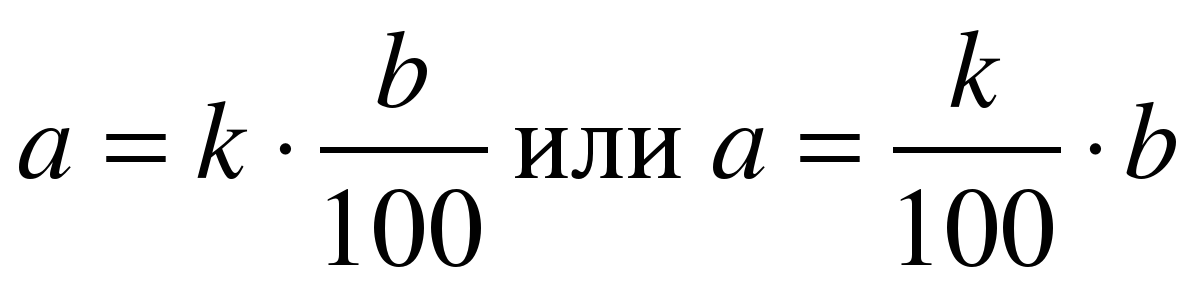
Последняя запись удобна тем, что одного взгляда достаточно для того, чтобы сказать, какой процент от числа в составляет число а.
Например из записи а = 0,61в сразу видно, что число а составляет 61% от числа в.
Практические задачи
Задача 1. Только 94% из 27500 выпускников города правильно решили задачу №1. Сколько человек правильно решили задачу №1?
Решение:
| 1 способ Примем 27500 выпускников за 100%. Составим пропорцию 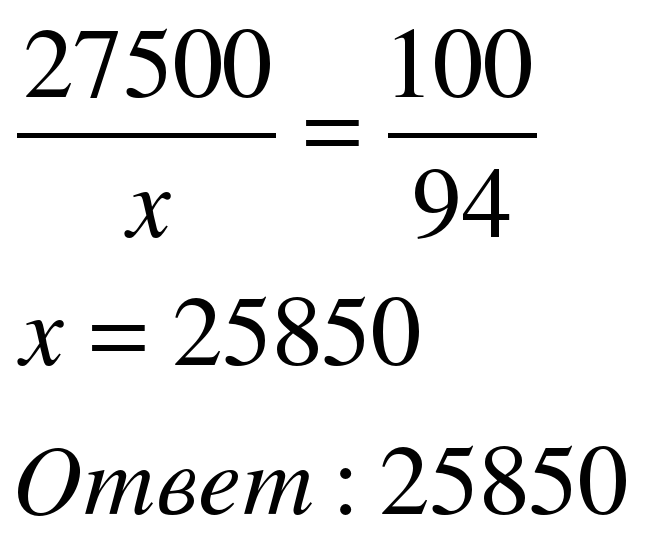
| 2 способ 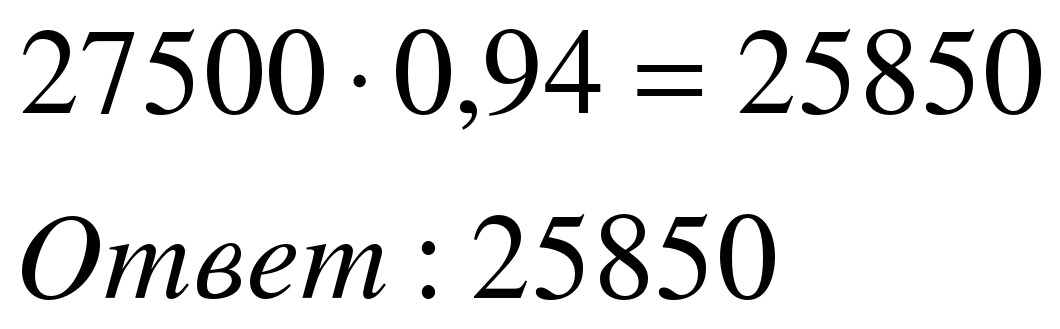
|
Задача 2. Призерами городской олимпиады по математике стали 48 учеников, что составило 12% от числа участников. Сколько человек участвовало в олимпиаде?
Решение:
| 1 способ Примем количество участников за 100%. Составим пропорцию 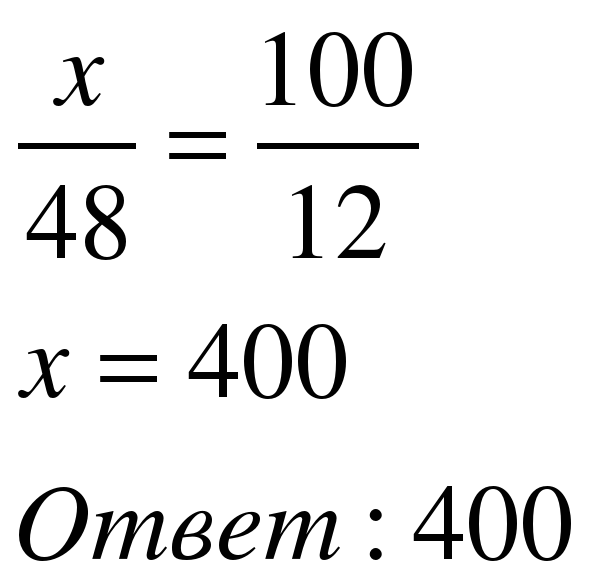
| 2 способ 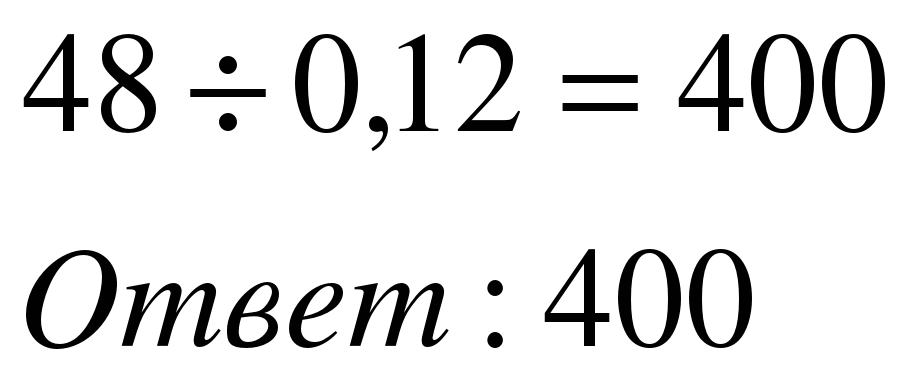
|
Задача 3. Число мальчиков в школе составляет 40% от общего числа учащихся. Каково процентное отношение числа девочек к числу мальчиков?
Решение:
| Примем количество учеников за а, тогда 0,4а – мальчики, 0,6а – девочки Составим отношение 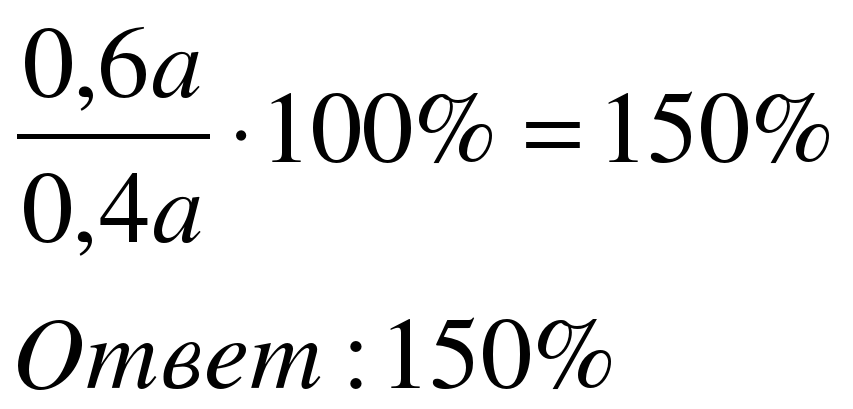
|
|
Задача 4. Один из договоров о годичном страховании имущества от несчастных случаев предусматривает оплату 2,16% страховой сумы при скидке 30% для постоянных клиентов. Определить величину страхового платежа для повторного страхования дачного домика на сумму 20 000 рублей?
Решение:
Задача 5. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
| Так как прибавление зарплаты мужа увеличивает общий доход семьи на 67%, то зарплата мужа составляет 67% от общего дохода семьи. Так как уменьшение стипендии дочери втрое соответствует уменьшению общего дохода семьи на 4%, то 2/3 стипендии дочери составляют 4% общего дохода семьи, вся стипендия дочери составляет 6% общего дохода. На долю зарплаты жены приходится 100% - 67% - -6% = 27% 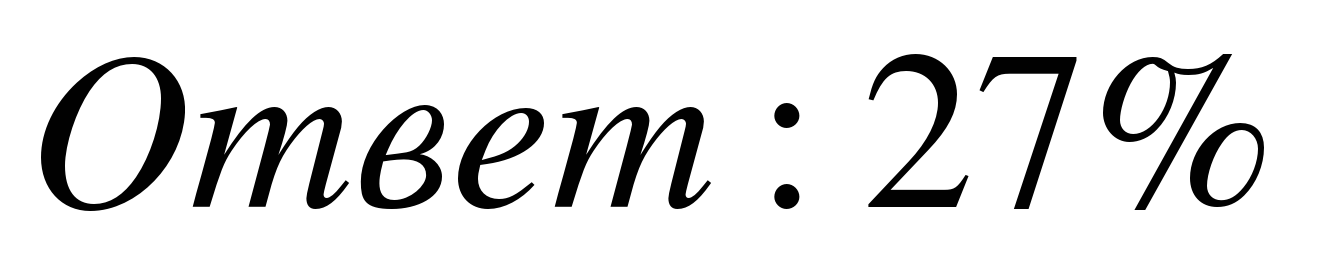
|
Занятие 2. «Решение задач на проценты».
Теоретический аспект
Процент – сотая доля (часть) целого.
Пусть число а составляет к % от числа в. Алгебраически это можно записать так
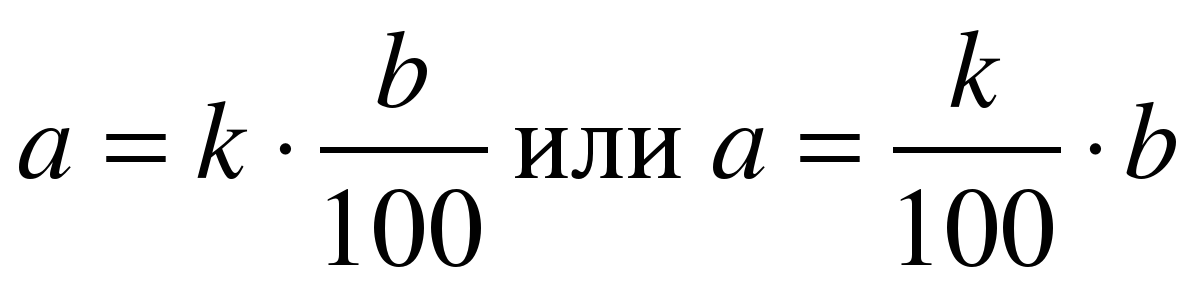
Последняя запись удобна тем, что одного взгляда достаточно для того, чтобы сказать, какой процент от числа в составляет число а.
Например из записи а = 0,61в сразу видно, что число а составляет 61% от числа в.
Практические задачи
Задача 1. Товар подорожал на 30%, а затем подешевел на 30%. Как изменилась цена товара?
Решение:
| Примем первоначальную цену товара за х, тогда 1,3х – новая цена (после подорожания на 30%), 0,7*1,3х = 0,91х – новая цена (после удешевления). 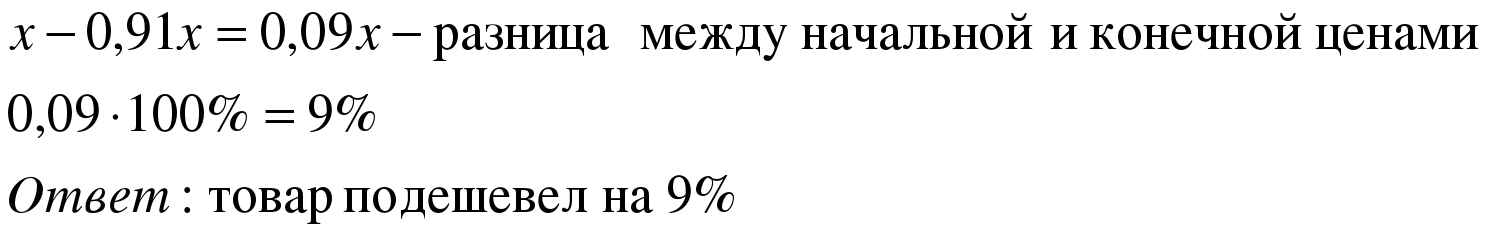
|
|
Задача 2. На первом заседании парламента присутствовало 40% от списочного состава депутатов, на втором – 55%. Сколько процентов депутатов присутствовало на обоих заседаниях?
Решение:
| В этой задаче нельзя дать определенный ответ. Если все присутствующие на первом заседании были и на втором, то на двух заседаниях было 40% депутатов. Если же никто из посетивших первое заседание не пришел на второе, то на двух заседаниях было 0% депутатов. Понятно, что пересечением этих групп может быть любое целое число депутатов от 0% до 40%.
|
|
Задача 3. Сколько нужно взять сливок жирностью 36% и жирностью 18%, чтобы получить 90 кг сливок с содержанием 30% жира?
Решение:
| Примем количество сливок с жирностью 36% за х, а с жирностью 18% - за y. Тогда 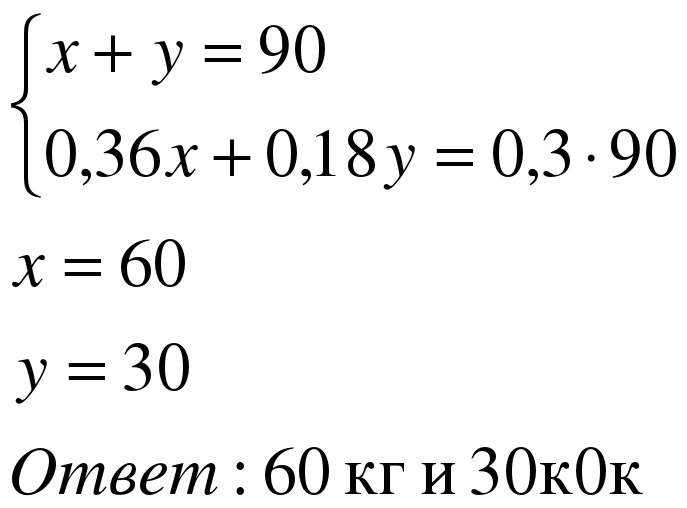
|
|
Задача 4. Товар подорожал на 10%, а затем еще на 20%. Как изменилась цена товара?
Решение:
| Примем первоначальную цену товара за х, тогда 1,1х – новая цена (после подорожания на 10%), 1,2*1,1х = 1,32х – новая цена (после подорожания на 20%). 
|
|
Задача 5. В растворе содержится 15 г сахара, 20 г соли и 165 г воды. Определите, каково процентное содержание соли и сахара в растворе?
Решение:
| Процентное содержание соли в растворе: 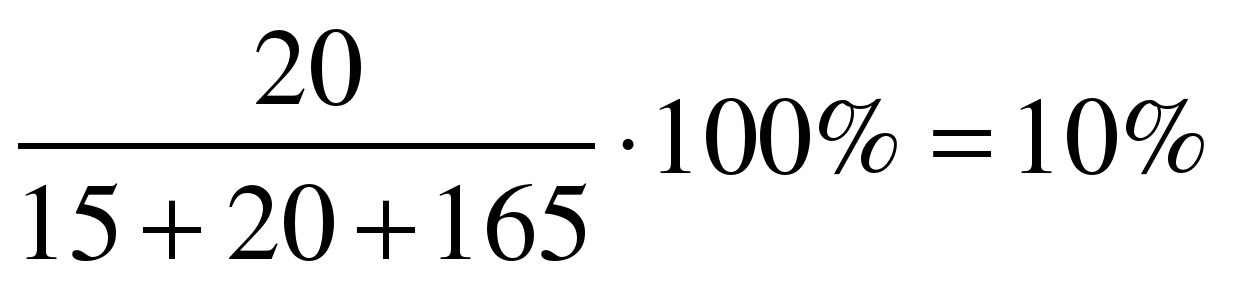 Процентное содержание сахара в растворе: 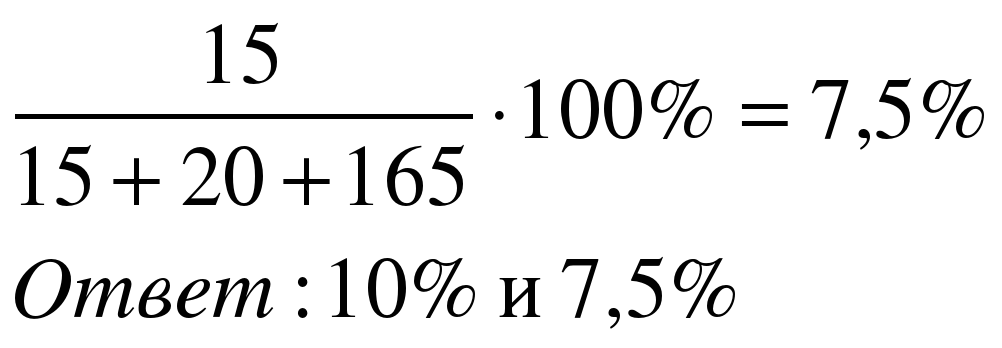
|
|
Дополнительные задачи (домашнее задание):
1. В бутылку с 20 г 72%-й уксусной эссенции добавили 140 г воды. Каково процентное содержание уксусной кислоты в получившемся растворе?
2. Магазин продал одному покупателю 25% полотна, второму – 30% остатка, а третьему – 40% нового остатка. Сколько процентов полотна осталось?
3. В одном городе Канады 70% жителей знают французский и 80% - английский язык. Сколько процентов жителей знают оба языка?
Занятие 3. «Процентное изменение величины».
Теоретический аспект
Пусть некоторая величина А, меняющаяся со временем, имеет в начальный момент значение А0, а через промежуток времени А1.
Если значение А1 больше (меньше) значения А0 на р%, то можно составить пропорцию:
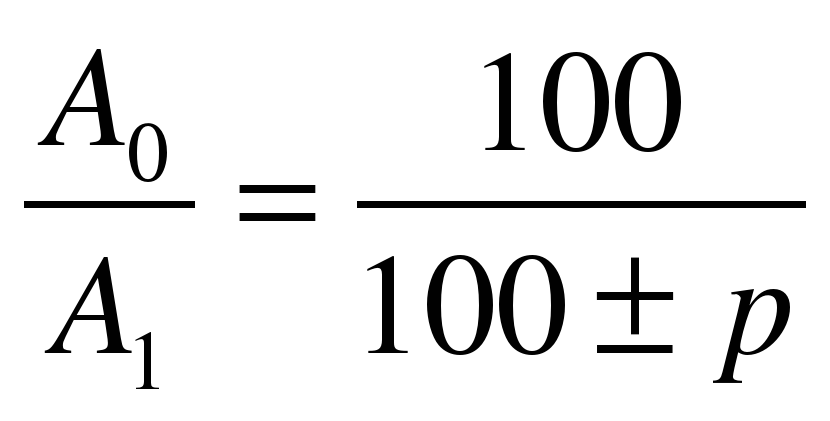
Из этого равенства можно выразить любую из переменных, в частности
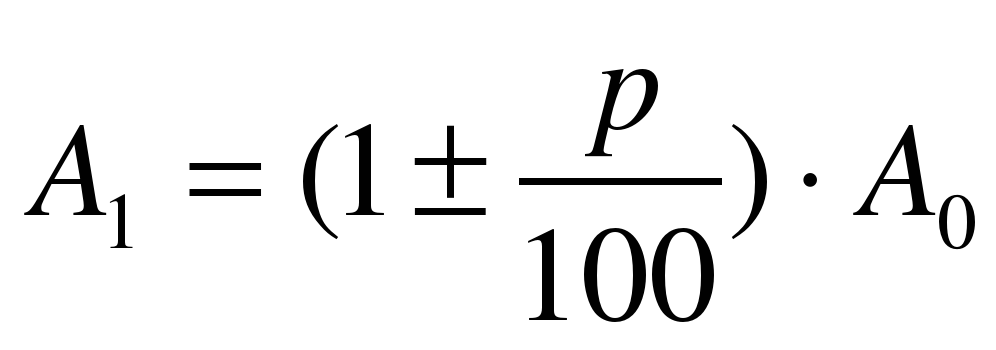
Величину р называют процентным «приростом» величины А.
Практические задачи
Задача 1. В сентябре 1кг слив стоил 60 рублей. В октябре сливы подорожали на 25%. Сколько рублей стоил 1кг слив после подорожания в октябре?
Решение:
| 1 способ Примем первоначальную цену 60 руб за 100%. Составим пропорцию 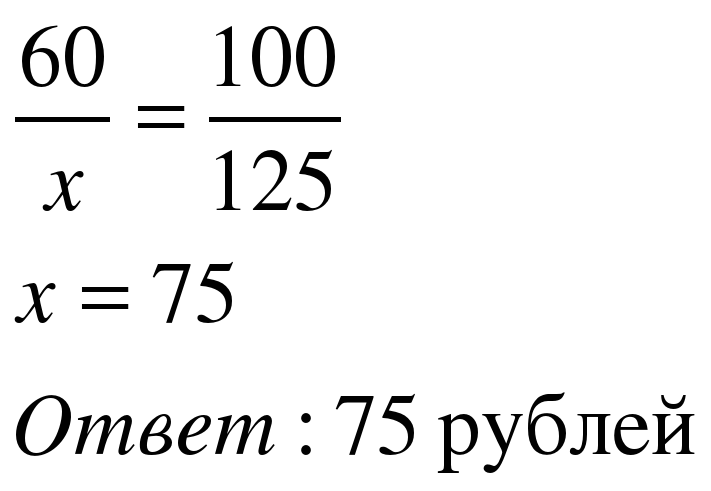
| 2 способ Применим формулу
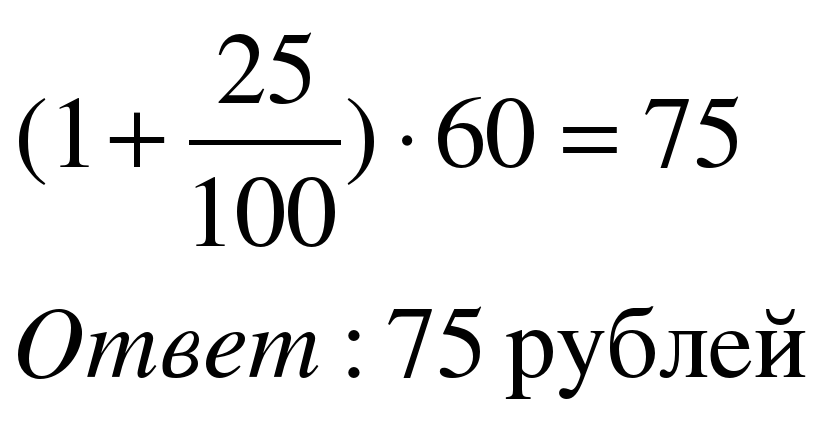
|
Задача 2. Налог на доходы составляет 13% от заработной платы. После удержания налога Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
Решение:
| 1 способ Примем заработную плату х рублей за 100%. Составим пропорцию 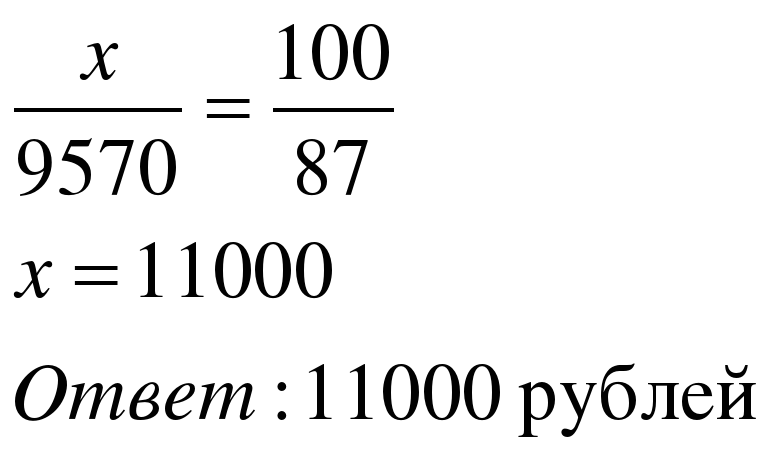
| 2 способ Применим формулу
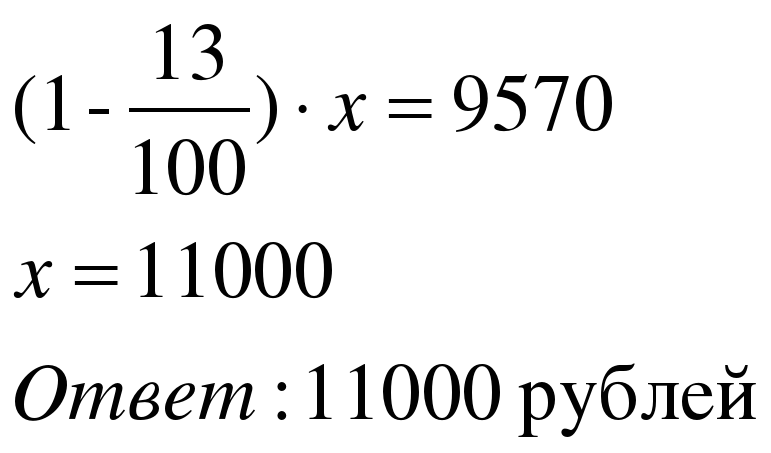
|
Задача 3. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Решение:
| 1 способ Примем цену футболки 800руб. за 100%. Составим пропорцию 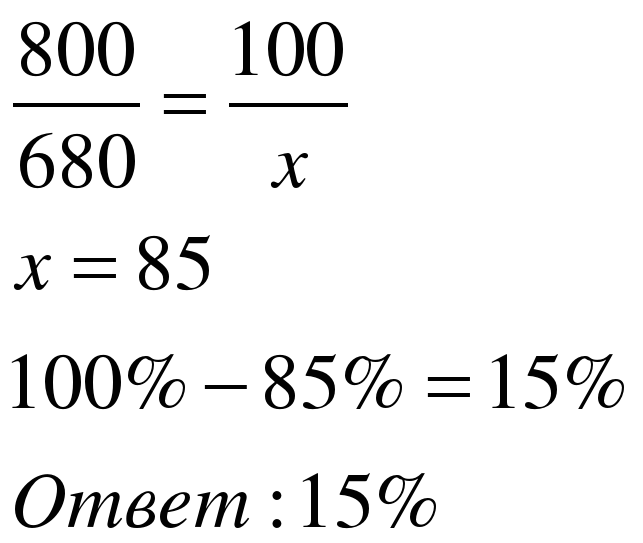
| 2 способ Применим формулу
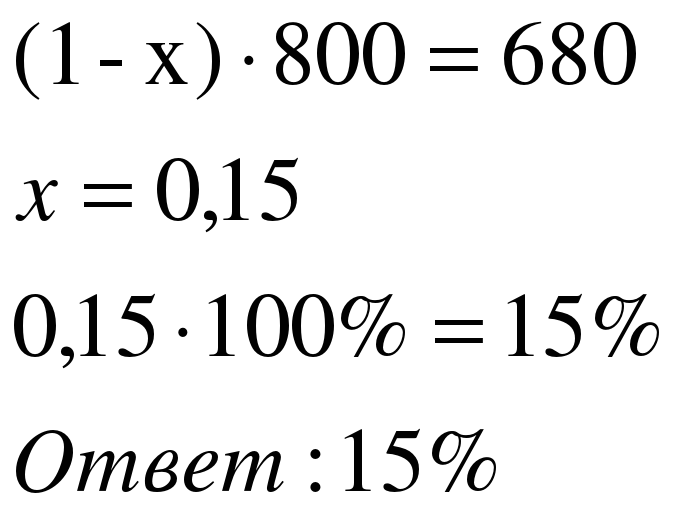
|
Задача 4. Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Решение:
| 1 способ
| 2 способ Применим формулу
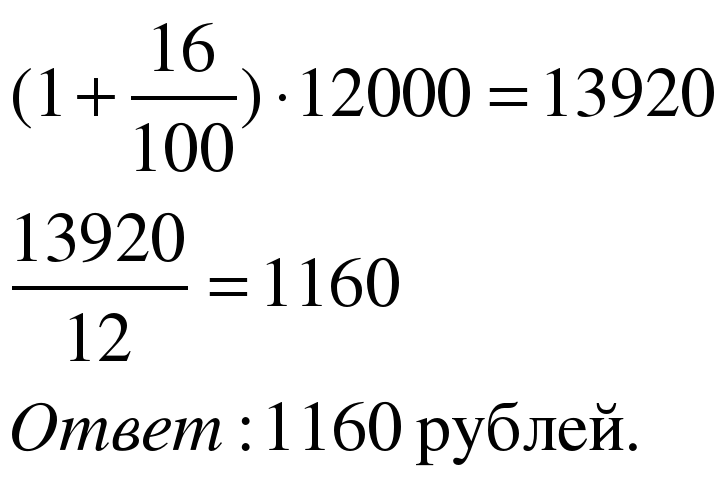
|
В некоторых задачах величины связаны формулой и ставится вопрос, как процентное изменение одних величин влияет на процентное изменение других величин.
Задача 5. За некоторый период времени количество акций Иванова увеличилось на 15%. На сколько процентов увеличилась общая стоимость акций Иванова, если цена каждой акции увеличилась на 20%?
Решение:
|
| Цена одной акции | Количество акций | Общая стоимость |
| Было | S0 | n | S0n |
| Стало | 1,2 S0 | 1,15n | 1,38 S0n |
Общая стоимость акций увеличилась в 1,38 раз, т.е на 38%.
Ответ: 38%.
Задача 6. Производительность труда рабочего при выполнении определенной работы увеличилась на 25%. На сколько процентов сократилось время для выполнения этой работы?
Решение:
|
| Работа | Производительность | Время |
| Было | А | N | 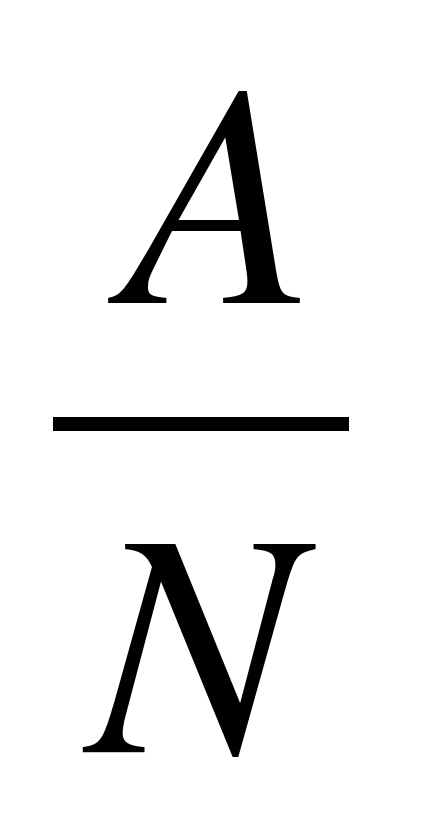
|
| Стало | А | 1,25N | 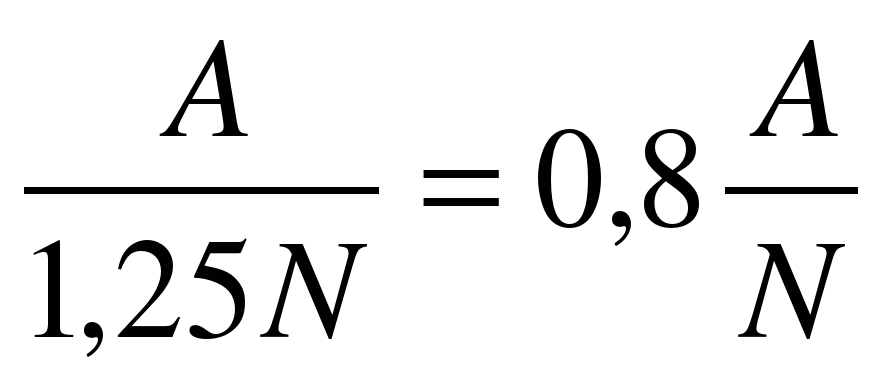
|
Новое время работы составило 80% от старого времени, т.е. сократилось на 20%.
Ответ: 20%.
Занятие 4. «Формула простых процентов».
Теоретический аспект
Если величина А через равные промежутки времени t1 имеет процентный прирост р только на первоначальное значение А0, то в момент времени tn = nt1 ее значение An будет равно.
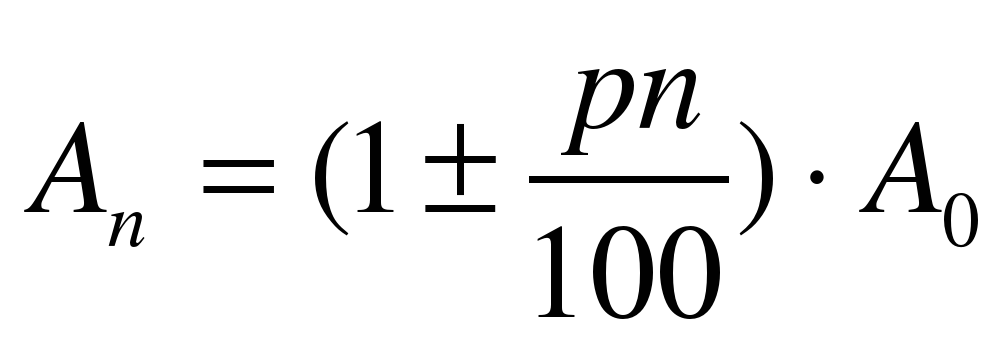
Формулу простых процентов используют, например, для начисления штрафов. Также удобно применять начисление простых процентов тогда, когда по истечении каждого года вкладчик снимает со своего счета проценты, начисленные за этот год.
Практические задачи
Задача 1. Занятия ребенка в музыкальной школе родители оплачивают в Сбербанке, внося ежемесячно 250 рублей. Оплата должна производиться до 15-го числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько денег придется заплатить родителям, если они просрочат оплату на неделю?
Решение:
Применим формулу
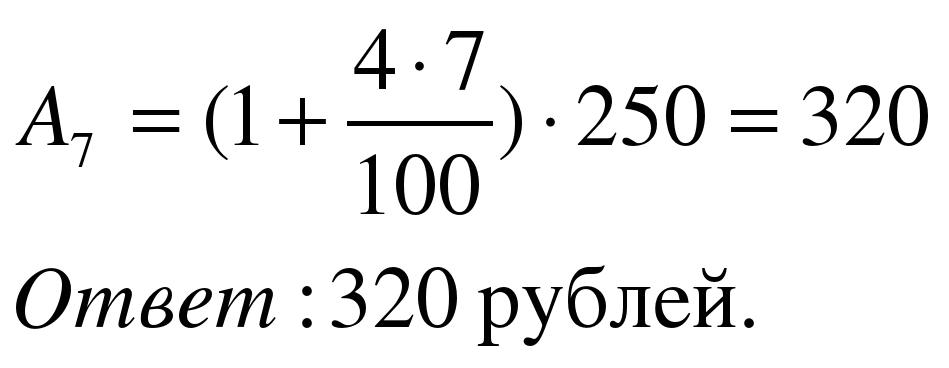
Задача 2. Какую сумму положили в банк под простые проценты по ставке 22% годовых, если через 5 лет вклад достиг 94500 рублей?
Решение:
Применим формулу
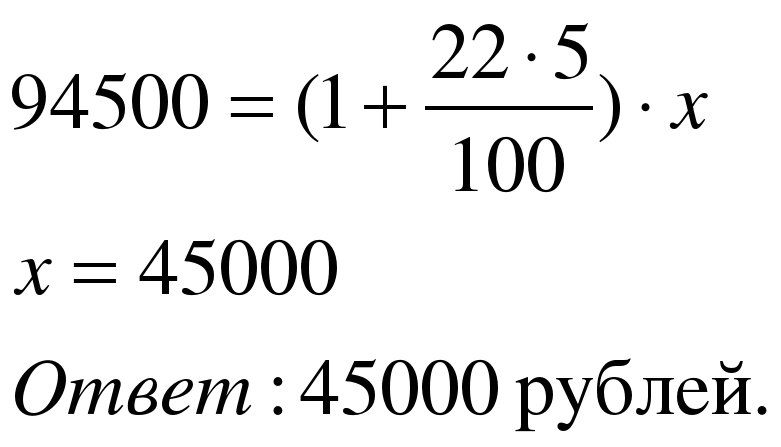
Задача 3. Сколько лет лежал в банке вклад 70 000 рублей, если по ставке 19,2% годовых простых процентов он достиг величины 150 640 рублей?
Решение:
Применим формулу
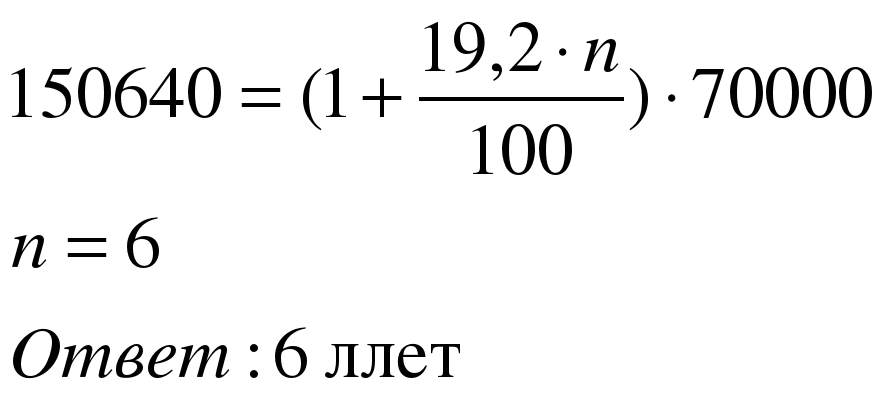
Задача 4. Какую годовую ставку простых процентов выплачивает банк, если вклад 12 000 рублей через 3 года достиг величины 14 160 рублей?
Решение:
Применим формулу
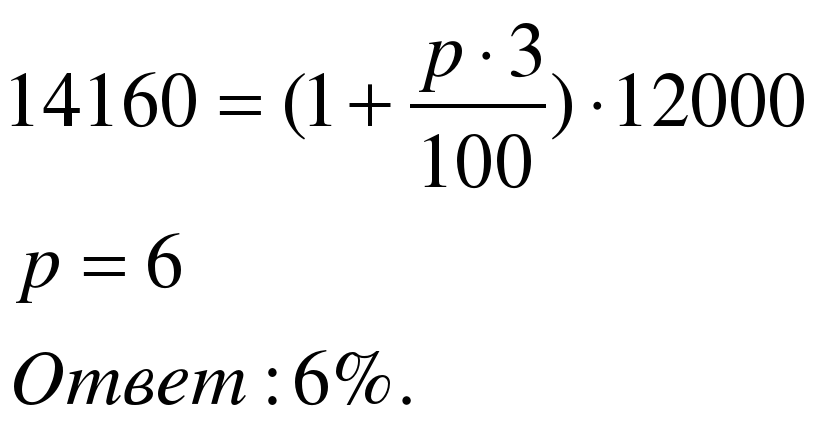
Занятие
5. «Формула сложных процентов».
Теоретический аспект
Если величина А через равные промежутки времени t1 имеет процентный прирост р, и процент начисляется на измененную величину, то в момент времени tn = nt1 ее значение An будет равно.
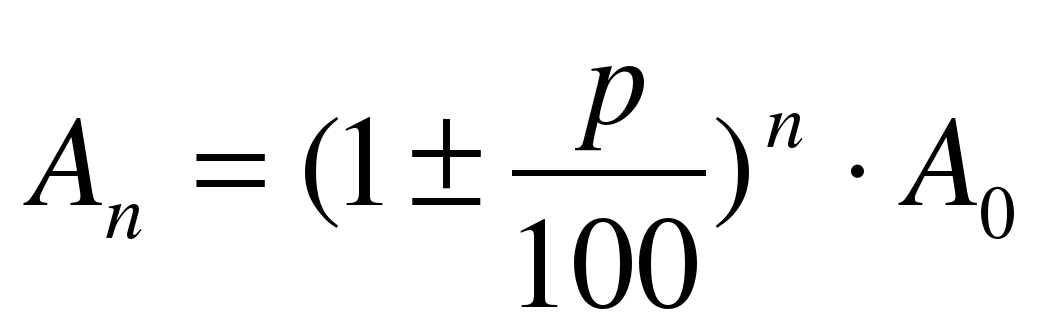
Практические задачи
Задача 1. Один из видов срочных вкладов предусматривает начисление 9% прибыли через год хранения денег в банке. Если спустя этот срок счет не закрывается, то договор автоматически продлевается на тех же условиях (пролонгируется). Какая сумма будет на счете через три года при первоначальном вкладе 17 000 рублей? Результат округлите до десятых.
Решение:
Применим формулу
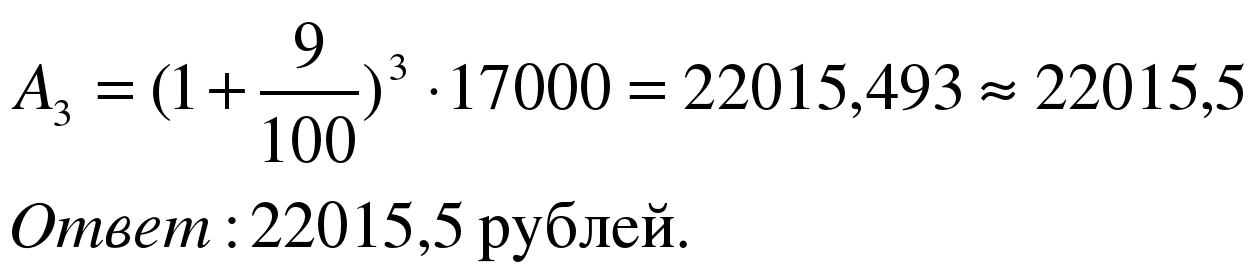
Задача 2. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определить, на сколько процентов каждый год уменьшалась цена, если холодильник, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рубля.
Решение:
Применим формулу
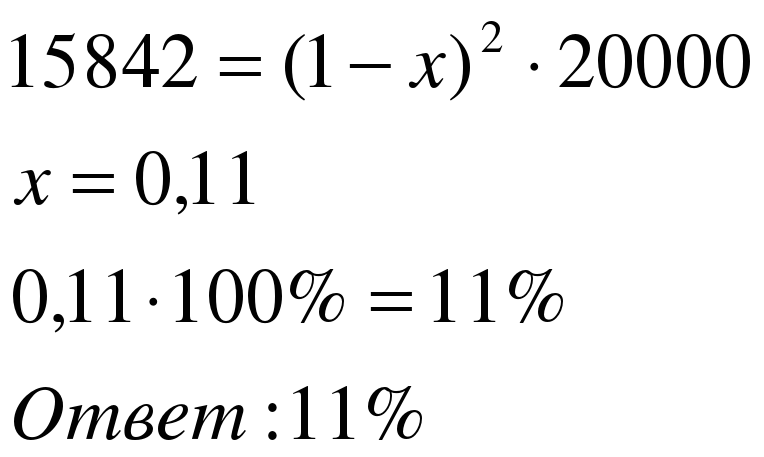
Задача 3. Начальный капитал акционерного общества составляет 15 млн рублей. Ежегодно капитал увеличивался на 25%. Найти минимальное количество лет, после котрых капитал акционерного общества превысит 45 млн рублей.
Решение:
Применим формулу
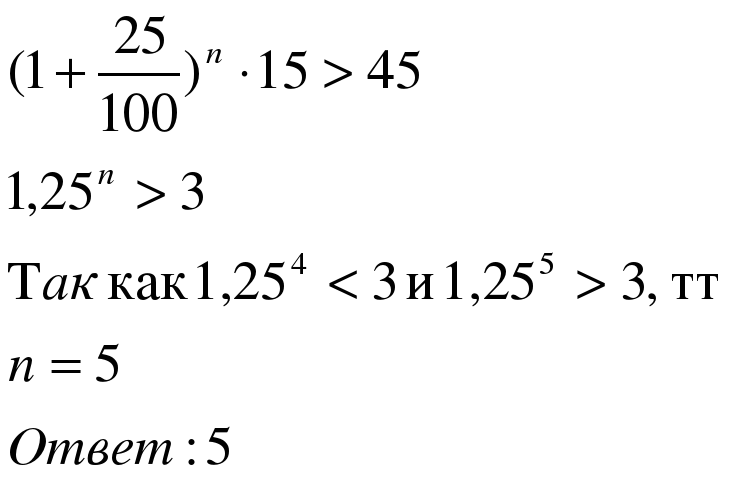
Задача 4. Клиент А сделал вклад в банк в размере 6200 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. еще ровно через год клиенты А и Б закрыли вклады и забрали все накопившиеся деньги. При этом клиент А получил на 682 рубля больше клиента Б. какой процент годовых начислял банк по этим вкладам?
Решение:
Применим формулу
|
| Через год | Через 2 года |
| Клиент А | 6200(1+х) | 6200(1+х)2 |
| Клиент Б | - | 6200(1+х) |
Составим уравнение
6200(1+х)2 - 6200(1+х) = 682
100(1+х)2 - 100(1+х) – 11 = 0
х = 0,1
0,1*100% = 10%
Ответ: 10%.
Занятие 6. «Кредиты».
Теоретический аспект
Кредит – это финансовая сделка, в результате которой кредитор предоставляет на определенный срок деньги заемщику. За пользование деньгами заемщик, кроме погашения основного долга, выплачивает проценты. Разделение погашающих платежей на две части, отвечающие за погашение долга и погашение процентных денег, принципиально важно, поскольку от этого зависят уплачиваемые налоги
Рассмотри две схемы погашения кредитов:
дифференцированная – разными платежами, убывающими в арифметической прогрессии;
аннуитетная – равными платежами.
При дифференцированной схеме ежемесячный платеж включает в себя постоянную сумму для погашения основного долга по кредиту к которому прибавляются проценты на оставшуюся часть долга. При этом регулярные платежи оказываются различными. Методика расчета платежей в этом случае базируется на использовании арифметической прогрессии. Процентный платеж за пользование кредитом обычно вычисляется «вперед»: для первого месяца процентный платеж рассчитывается на всю величину долга, а в каждый следующий месяц – на остаток долга, т.е. величину долга, уменьшенную на уже выплаченную часть.
Если К – величина кредита,
m – число одинаковых месячных выплат,
p – годовая процентная ставка, то
платеж в первом месяце составит
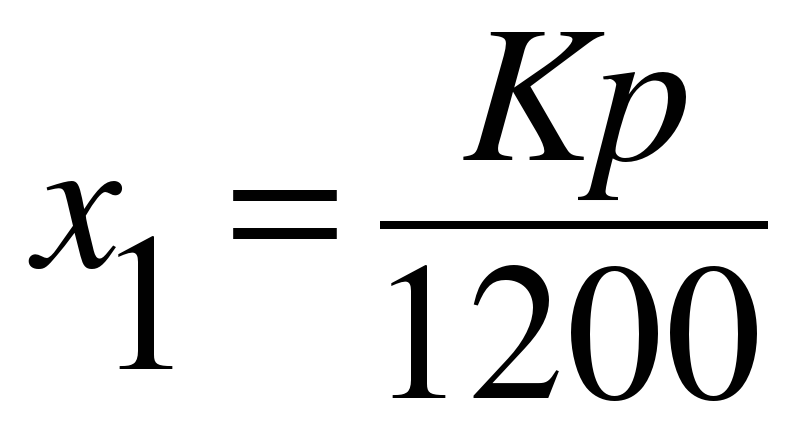
во втором:
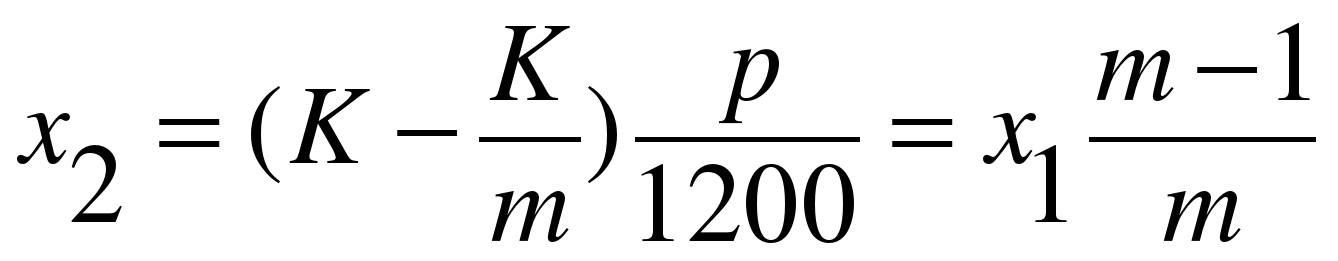
в третьем:
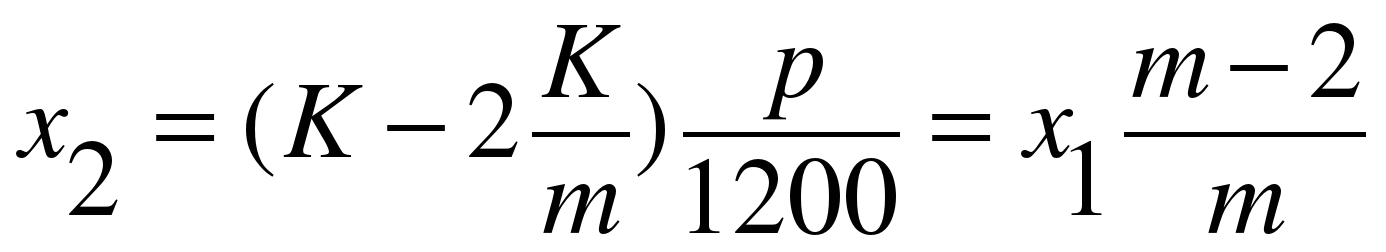
в m–ом месяце:
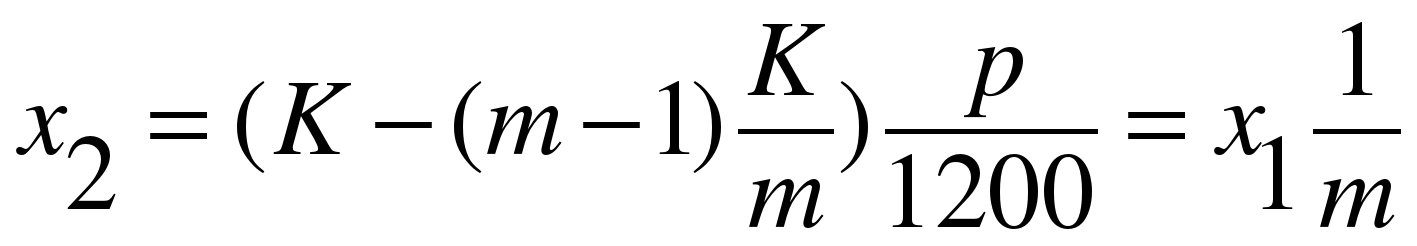
Общая величина выплат за пользование предоставленным кредитом равна сумме всех процентных платежей:
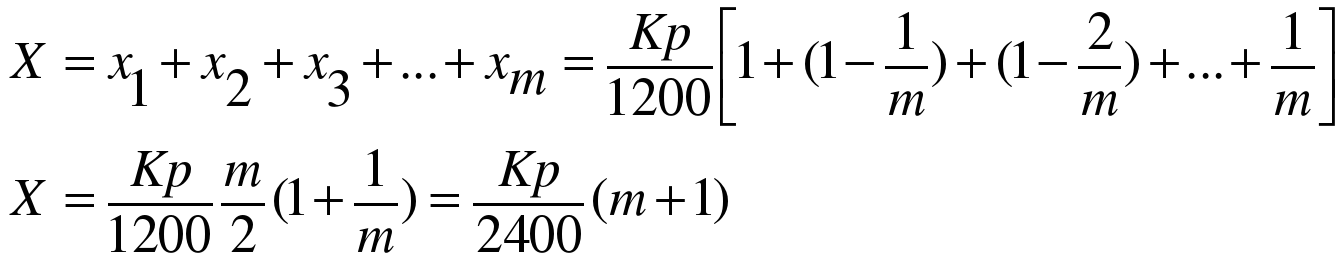
Аннуитетная схема: сумма ежемесячного платежа фиксируется на весь срок кредитования.
Если S – величина кредита,
n – число лет,
p – годовая процентная ставка,
x - ежегодный платеж по кредиту, то
полная выплата по кредиту составит Х = nx рублей.
Найдем х и Х для n = 3.
Ежегодное начисление р% на остаток долга соответствует умножению на коэффициент q = 1+0,01р.
После первой выплаты сумма долга составит:
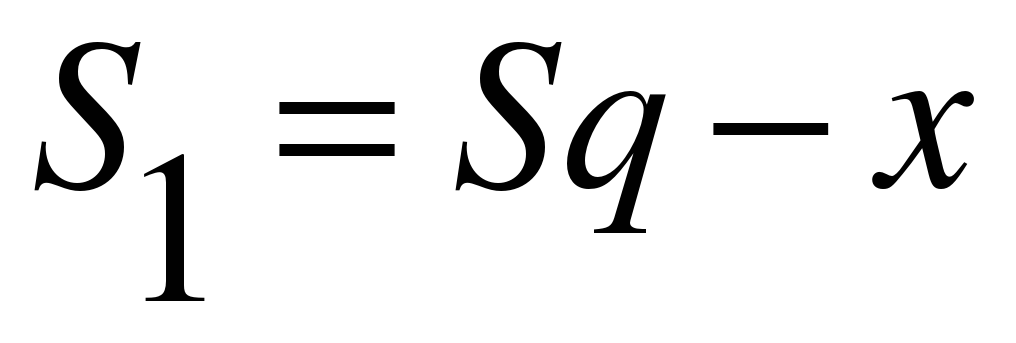
После второй:
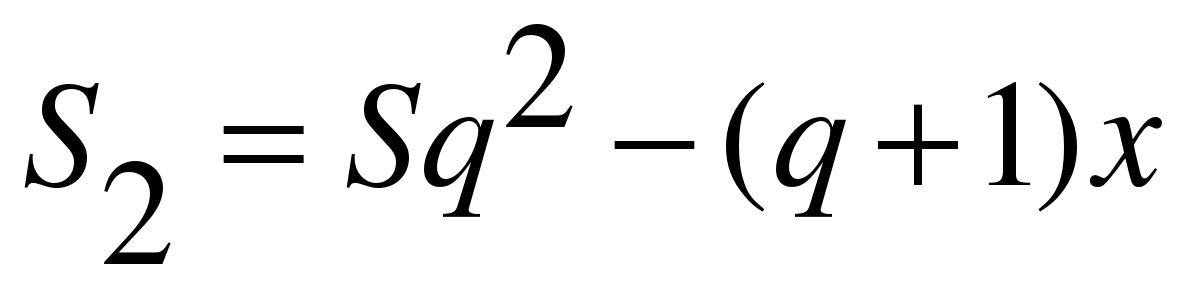
После третьей:
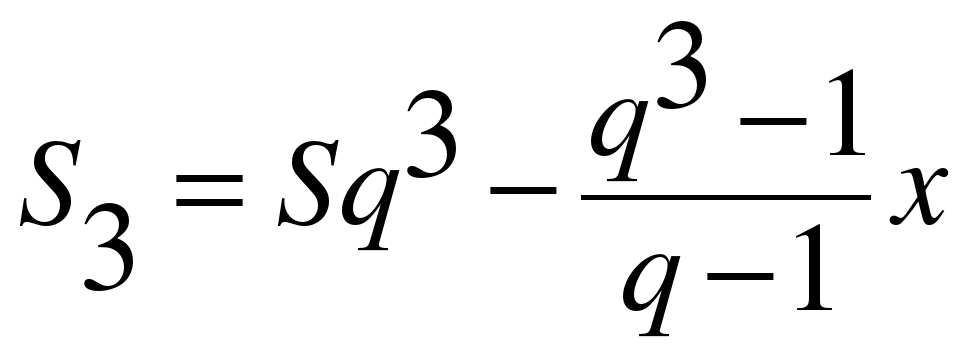
Если n = 3, то S3 = 0. Тогда полная выплата по кредиту составит
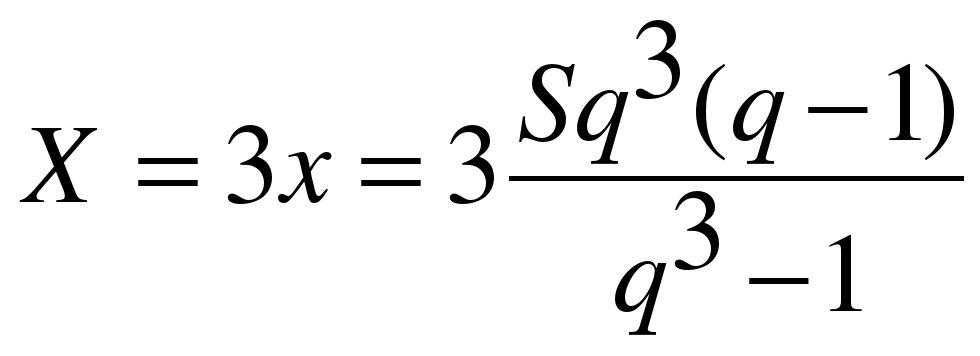
Практические задачи
Задача 1. 31 декабря 2014 года Сергей взял в банке 8 420 000 рублей в кредит под 10,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивается долг на 10,5%), затем Сергей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Сергей выплатил долг двумя равными платежами?
Решение:
Пусть S – сумма кредита,
Х– ежегодный платеж,
а% - годовые проценты.
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a
Сумма долга после первой выплаты:
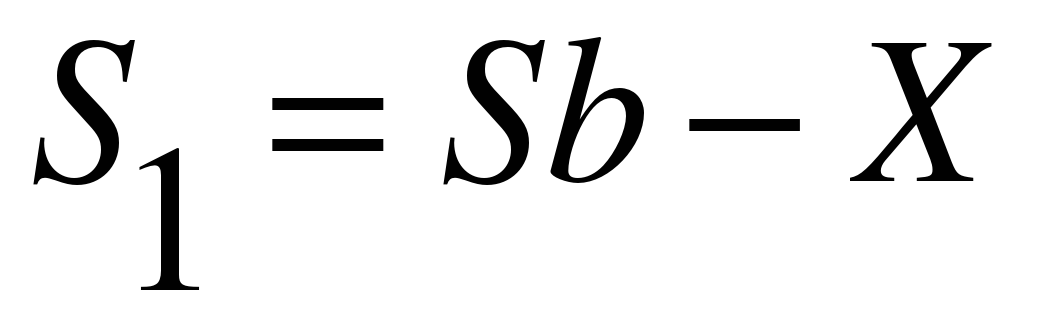
Сумма долга после второй выплаты:
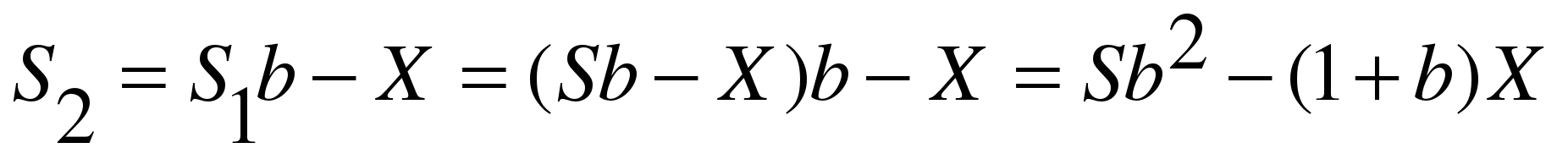
По условию двумя выплатами Сергей должен погасить кредит полностью, значит
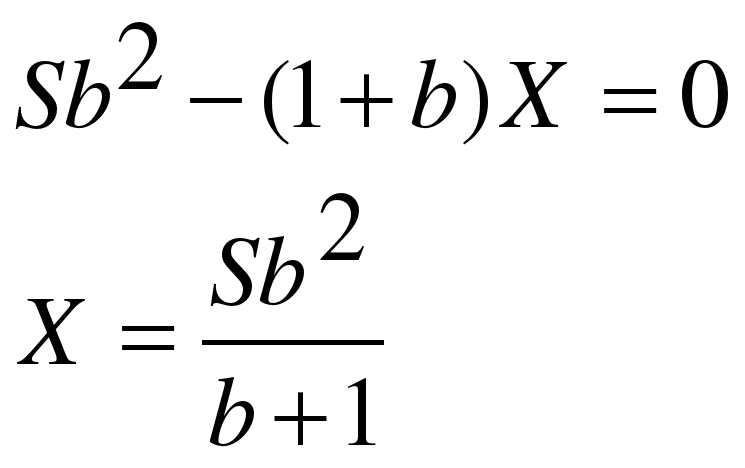
При S = 8 420 000, a = 10,5 получаем
b = 1,105
X = 4 884 100
Ответ: 4 884 100 рублей.
Задача 2. 31 декабря 2014 года Алексей взял в банке 9 282 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивается долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами?
Решение:
Пусть S – сумма кредита,
Х– ежегодный платеж,
а% - годовые проценты.
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a
Сумма долга после первой выплаты:
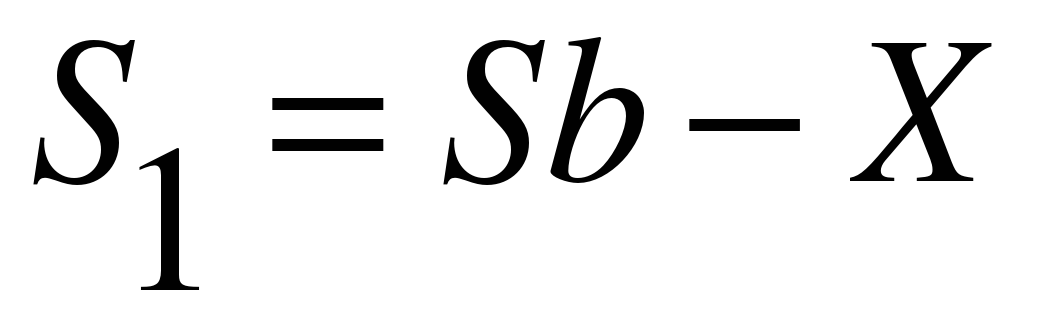
Сумма долга после второй выплаты:
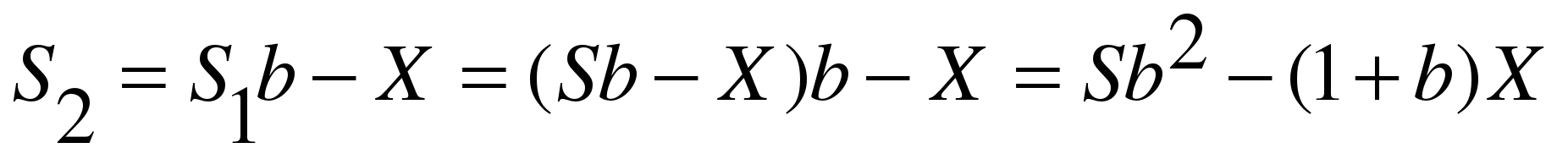
Сумма долга после третьей выплаты:
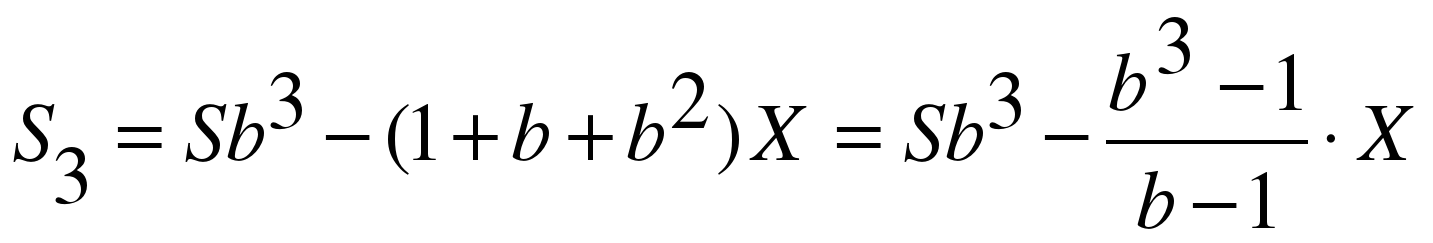
Сумма долга после четвертой выплаты:
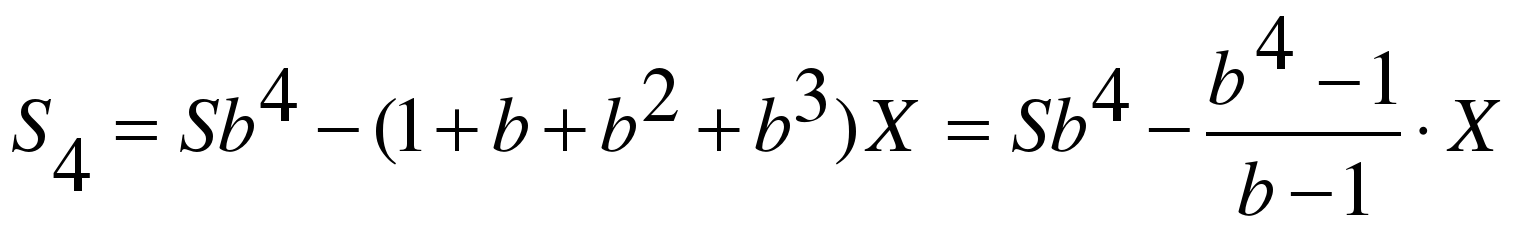
По условию четырьмя выплатами Алексей должен погасить кредит полностью, значит
При S = 9 282 000, a = 10 получаем
b = 1,1
X = 2 928 200
Ответ: 2 928 200 рублей.
Задача 3. 31 декабря 2014 года Арсений взял в банке 1 млн.рублей в кредит. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй – 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?
Решение:
Пусть S – сумма кредита,
Х– первый платеж,
Y – второй платеж,
а% - годовые проценты.
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a
Сумма долга после первой выплаты:
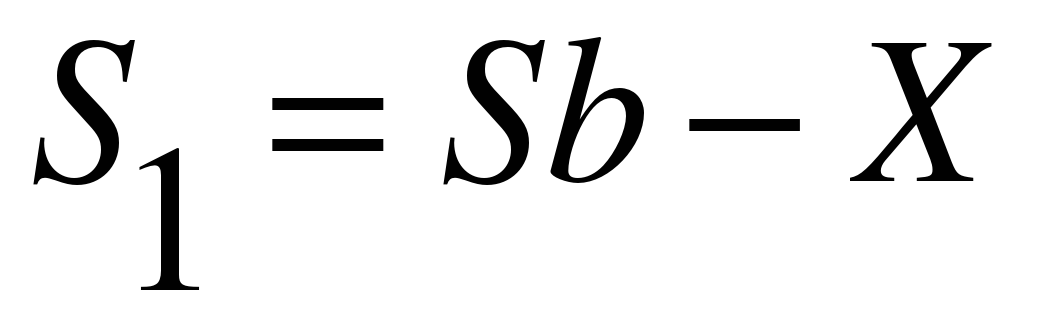
Сумма долга после второй выплаты:
По условию двумя выплатами Арсений должен погасить кредит полностью, значит
Ответ: 12%.
Задача 4. Матвей хочет взять в банке кредит 1,4 млн.рублей. Схема выплаты кредита следующая – раз в год равными суммами (кроме, может быть, последней) после начисления процентов. На какое минимальное количество лет может Матвей взять кредит, чтобы ежегодные выплаты были не более 320 тыс.рублей.?
Решение:
Пусть S – сумма кредита,
Х– ежегодный платеж,
а% - годовые проценты.
В последний день каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a
Составим таблицу выплат.
| Год | Долг банку (руб.) | Остаток после транша (руб.) |
| 0 | 1 400 000 | --- |
| 1 | 1 540 000 | 1 220 000 |
| 2 | 1 342 000 | 1 022 000 |
| 3 | 1 124 200 | 804 200 |
| 4 | 884 620 | 564 620 |
| 5 | 621 082 | 301 082 |
| 6 | 331 190,2 | 11 190,2 |
| 7 | 12 309,22 | 0 |
Ответ: 7 лет.
Задача 5. 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 20%), затем Тимофей переводит в банк платеж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение:
Пусть S – сумма кредита,
Х, Y – ежегодный платеж,
а% - годовые проценты.
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a
Сумма долга после первой выплаты:
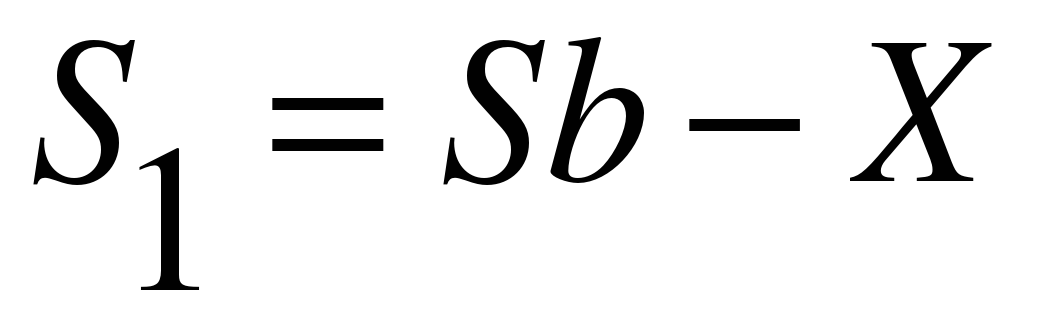
Сумма долга после второй выплаты:
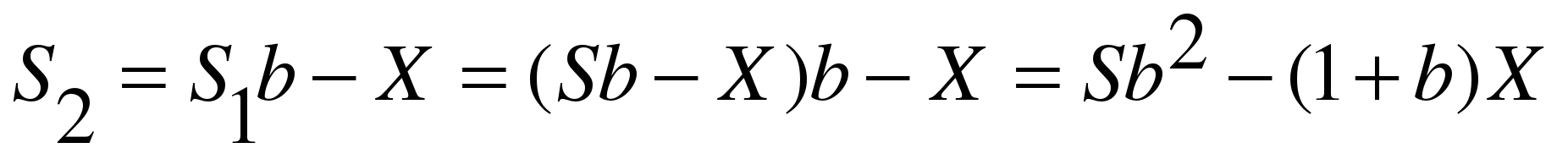
Сумма долга после третьей выплаты:
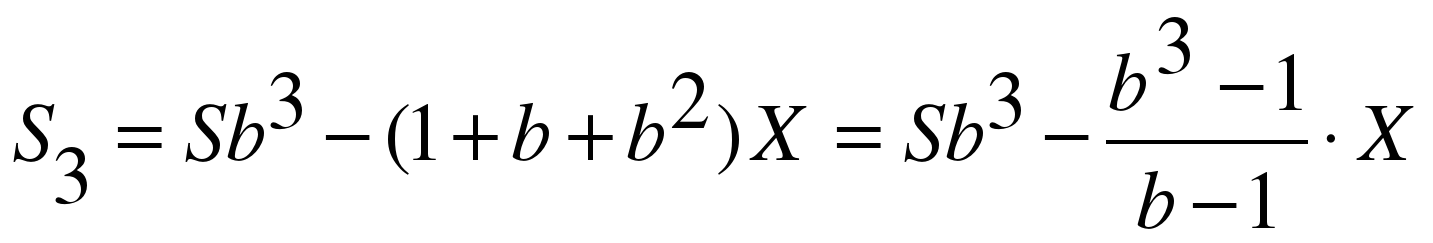
По условию тремя выплатами Тимофей должен погасить кредит полностью, значит
Аналогично, находи, что если бы Тимофей гасил долг двумя равными платежами, то каждый год он должен был бы выплачивать
Значит, он отдал банку на 3Х – 2Y рублей больше.
При S = 7 007 000, a = 20 получаем
b = 1,2
X = 3 326 400
Y = 4 586 400
3Х – 2Y = 806 400
Ответ: 806 400 рублей.
Дополнительные задачи:
Предприниматель обратился в банк с просьбой о предоставлении ссуды в размере 1 000 000 рублей сроком на 1 год. Банк выделил ссуду с годовой процентной ставкой в 20% при условии погашения ссуды одним платежом в конце срока. Какую сумму должен через год возвратить предприниматель банку? Какие процентные деньги получит банк? (Ответ: 1 200 000, 200 000 рублей)
Клиент взял в банке кредит 18 000 рублей на год под 14%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? (Ответ: 1710 рублей)
20 декабря 2014 года Сергей взял в банке 800 000 рублей в кредит. План выплаты кредита: 20 числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга, затем Сергей переводит в банк платеж. На какое минимальное количество месяцев Сергей может взять кредит, чтобы ежемесячные выплаты были не более 360 000 рублей? (Ответ: 3 месяца)
Клиент взял 15 960 000 рублей в кредит под 30% годовых. По истечении к5аждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем клиент переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы клиент выплатил долг тремя равными ежегодными платежами? (Ответ: 8 788 000 рублей)
25 ноября 2013 года Иван взял в банке 2 млн. рублей в кредит. План выплаты кредита: 25 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга, т.е. увеличивает долг на х%, а затем Иван переводит очередной транш. Иван выплатил кредит за два транша, переведя в первый раз 1 210 000 рублей, а во второй – 1 219 800 рублей. Под какой процент банк выдал кредит Ивану? (Ответ: 14%)
Банк выдал заемщику кредит в размере 30 000 рублей, ежегодная выплата по кредиту составляет 10 000 рублей (последний платеж может отличаться от остальных в меньшую сторону), процентная ставка – 20% годовых. Через сколько лет кредит будет погашен? Сколько составит переплата? (Ответ: 5 лет, 18 528 рублей)
31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивается долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергею выплатить долг тремя равными ежегодными платежами? (Ответ: 3 993 000 рублей)
1 января 2015 года Александр Сергеевич взял в банке 1,1 млн.рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга, затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс.рублей.? (Ответ: 5 месяцев)
31 декабря 2014 года Владимир взял в банке некоторую сумму в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивается долг на 14%), затем Владимир переводит в банк 4 548 600 рублей. Какую сумму взял Владимир в банке, если он выплатил долг двумя равными платежами (т.е. за два года)? (Ответ: 7 490 000 рублей)
31 декабря 2014 года Антон взял в банке 1 млн.рублей в кредит. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на определенное количество %), затем Антон выплатил кредит за два транша: в первый раз 510 тыс.рублей, во второй – 649 тыс.рублей. под какой процент банк выдал кредит Антону? (Ответ: 10%)