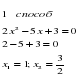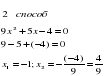| Опрос учащихся по заданному на дом материалу Мотивация к учебной деятельности Актуализация опорных знаний | Коммуникативные УУД
Познавательные
Регулятивные | Формирование умения слушать, понимать других
Формирование умения самостоятельно организовывать взаимодействие работы в паре , группе сотрудничества с учителем и сверстниками
Формирование умения анализировать, сравнивать , обобщать, делать выводыОсознанное вхождение учащегося в пр-во уч. деят-ти: Целеполаганиепланирование уч . Актуализация соотв.мыслит. операций и познавательных процессов: использование знаково-символических средств ,анализ,синтез,сравнение,фиксирование индивидуального затруднения в действиях(Р). | I - Придумайте вопросы к этому уравнению 3x² - 2x – 5 = 0 ( слайд 3) II - Блиц – опрос ( слайд 4) 1. Как называется выражение вида b²-4ac? 2. Сколько корней имеет квадратное уравнение при D = 0? 3. Какое максимальное число корней может иметь квадратное уравнение? В каком случае? 4. Какое квадратное уравнение называется приведенным? 5. Какое уравнение называется неполным квадратным? 6. Сколько корней может иметь биквадратное уравнение? (Ставим оценки) Какими способами можно решить квадратное уравнение? О чем мы сегодня будем говорить? какие поставим перед собой цели? . Повторим известные и ознакомимся с новым способом. Чтобы окунуться в мир решения квадратных уравнений должны получить пригласительные билеты. Билеты лежат на партах, нужно заполнить пропуски Хотя и допустили ошибки приглашаем всех в мир решений потренироваться (Ставим оценки) Интерактивная игра Игра Соответствие Найди пару (1 человек) 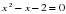 Разделимся на группы, Каждая группа будет решать уравнение своим способом , а потом сверим ответы, как только группа заканчивает решение уравнения выходит один человек к доске и пишет решение, остальные члены группы приступают к следующему уравнению. Разделимся на группы, Каждая группа будет решать уравнение своим способом , а потом сверим ответы, как только группа заканчивает решение уравнения выходит один человек к доске и пишет решение, остальные члены группы приступают к следующему уравнению.
3х2+2х-1=0 1 гр Метод разложения на множители ( слайд 7,8) • Метод разложения на множители. Цель: Привести квадратное уравнение общего вида к виду А(х)•В(х)=0, где А(х) и В(х) – многочлены относительно х.Способы: • Вынесение общего множителя за скобки; • Использование формул сокращенного умножения; • Способ группировки. или
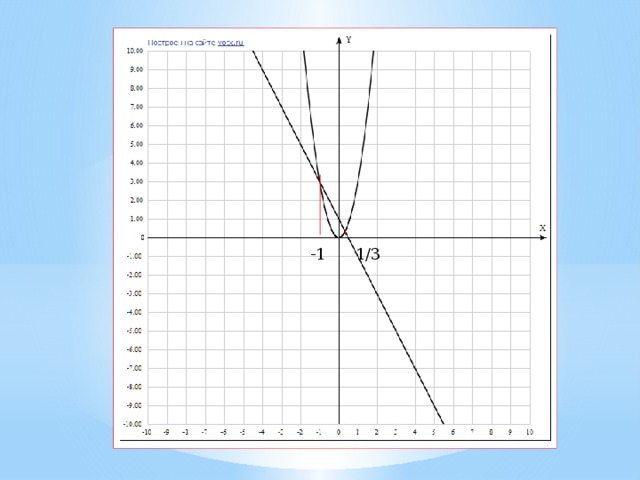
2 гр по формуле 3 гр Графический метод Графический метод ( слайд 9,10)Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x), y = g(x) и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения. 3х2+2х-1=0Вспомним применение этого метода при решении квадратного уравнения:(Устно обсудить области определения ) Применяя графический метод в данном случае мы нашли одно точное значение корня, а одно приблизительное, поэтому невсегда удобно. Однако, графический метод часто применяют не для нахождения корней уравнения, а для определения их количества. Выводы Проверка по слайдам. (Ставим оценки) ( слайд 12) Слайд общий Методы решения . Какие методы мы уже знаем? Какие новые? Фронтальная работа у доски 1. Выделение полного квадрата ( слайд 14) Метод выделения квадрата двучлена. Цель: Привести уравнение общего вида к неполному квадратному уравнению. В этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности: .
2. Метод замены переменной ( слайд 13) Метод введения новой переменной. Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной. Посмотрите, нельзя ли записать уравнение проще, введя новую переменную Физкультурная минутка для глаз и для улучшения мозгового кровообращения. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4-5 раз. Крепко зажмурить глаза (считая до 3), открыть, посмотреть вдаль (считая до 5). Повторить 4-5 раз. Исходное положение -сидя на стуле, 1-2-плавно наклонить голову назад, 3-4 голову наклонить вперед, плечи не поднимать. Повторить 4-6 раз. Темп медленный. Отдохнули, внимание
| Работа в парах. Две пары девочек работают по карточкам. Остальные внимание на экран. Работа устная по слайду
Ставят оценки
Решать уравнения будем разными способами
Дети ставят цели
Учащиеся заполняют пригласительные билеты, организуется взаимопроверка по слайду
Ставят оценки
1 человек работает у интерактивной доски Работа в группах. Решают уравнение, оформляют решение у доски
1 группа
Пример: решите уравнение 3х2+2х-1=0 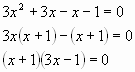
произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю. 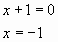 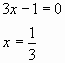
Ответ: -1; 1/3. 2 группа по формуле 3 группа графическим методом Построим график функции y=3х2Графиком является парабола, “ветви” которой направлены вверх (0;0) – вершина параболы график симметричен относительно оси ординат X -3 -2 -1 0 1 2 3 Y 27 12 3 0 3 12 27 Построим график функции y =-2 x +1Линейная функция. Графиком является прямая. X 0 -2 Y 1 5 Точки пересечения: А(-1;3) и В(1/3;1/3) Ответ: -1;1/3
Ставят оценки
Дети работают у доски Решим уравнение х2-6х+8=0 методом выделения квадрата двучлена. или Ответ: 2;4. 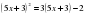 Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения
Пример решите уравнение Пусть: t = 5х + 3 Произведем замену переменной (проверим условие D 0) t1 = 1, t2 = 2 Произведем обратную замену и вернемся к переменной х Если t = 1, то Если t = 2, то Ответ: -0,4; -0,2 Вывод: при решении уравнения не следует торопиться выполнять преобразования. Учащиеся выполняют упражнения | Работа в парах, практический , общедидактический метод
Прием рассуждения, словесный метод
Практический метод, наглядный, дидактический
Метод контроля
Практический метод, наглядный, IT
Найти пару
http://LearningApps.org/display?v=poa55auoj01
Самооценка
Практический, поисковый
Практический, поисковый
Здоровьесбережение ( физкультминутка) |
| Объяснение нового материала
| Познавательные
Коммуникативные | Формирование исследовательских навыков уч-ся, постановка цели, выбор способа решения, построение плана достижения цели: постановка и формулировка проблемы
учет разных мнений, координирование в сотрудничестве разных позиций | 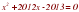 Решить уравнение Решить уравнение
Новый спосб с помощью коэффициентов ( слайд 16) Новая тема: 1. правило Пусть дано квадратное уравнение ( слайд 17) ах2 + bх + с = 0, где а ≠0. Свойство 1. Если а + b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/а Свойство 2. Если а – b + с = 0, или b = а + с, то х1 = – 1, х2 = – с/а 2.решение ( слайд 18) 3 показ слайдов3 | Проблема. Слишком большие коэффициенты. Первичное восприятие, усвоение нового теоретического материала
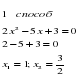
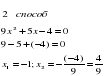
Записывают решение | Проблемный метод
Словесный (объяснение)
|
| Закрепление учебного материала Применение теоретических положений в условиях выполнения упражнений и решения задач Самостоятельное творческое использование сформированных навыков | Познавательные
Регулятивные
Познавательные
Коммуникативные
Познавательные
Регулятивные |
Развитие навыков самостоятельного решения задач : выполнение действий по алгоритму,анализ,сравнение,обобщение, контроль,коррекция,оценка,волевая саморегуляция в ситуации затруднения
Формирование исследовательских навыков уч-ся, постановка цели, выбор способа решения, построение плана достижения цели: постановка и формулировка проблемы,
учет разных мнений, координирование в сотрудничестве разных позиций,аргументация своего мнения и позиции в коммуникации,
моделирование и преобразование моделей,выполнение действий по образцу,установление причинно-следственных связей
Развитие навыков самостоятельного решения задач : выполнение действий по алгоритму,анализ,сравнение,обобщение, контроль,коррекция,оценка,волевая саморегуляция в ситуации затруднения | Работа по вариантам ( слайд 19) Проверка (Ставим оценки) ( слайд 20) Что значит решить уравнение? -А Вам необходимо угадать, что же находится в ящике. ( слайд 21) Математика и биология Учитель: Угадайте, что в ящике. Даю три определения этому предмету: 1. Непроизводная основа слова. 2. Число, которое после постановки его в уравнение обращает уравнение в тождество. 3. Один из основных органов растений Итог корень. Правильно. Итак за вашу работу вам подарок. Вы хорошо поработали, молодцы. ( слайд 22) Роза в подарок. Роза королевский цветок, о которой в народе говорят: "Цветы ангельские, а когти дьявольские". О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой. Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Мы увидели, что слово "корень" встречается на уроках биологии и математики. И не только. Расслабились, сейчас снова наберемся сил, вооружимся знаниями и выполним тест в тетрадях, а затем их сдадим. Тест Тема «Решение квадратных уравнений»
| Дети решают уравнения по вариантам, проверяют, возвращаются к проблемному уравнению
Ставят оценки.
/Корень/
Выполняют тест в тетрадях Ставят оценки | Практический
Метод контроля
Наглядный, словесный ( рассказ)
Практический, поисковый, проблемный, метод контроля |
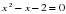 Разделимся на группы, Каждая группа будет решать уравнение своим способом , а потом сверим ответы, как только группа заканчивает решение уравнения выходит один человек к доске и пишет решение, остальные члены группы приступают к следующему уравнению.
Разделимся на группы, Каждая группа будет решать уравнение своим способом , а потом сверим ответы, как только группа заканчивает решение уравнения выходит один человек к доске и пишет решение, остальные члены группы приступают к следующему уравнению.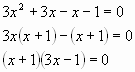
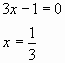
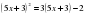 Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения
Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения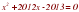 Решить уравнение
Решить уравнение