"Решение тригонометрических уравнений". С использованием ИКТ, проектной технологии и АМО

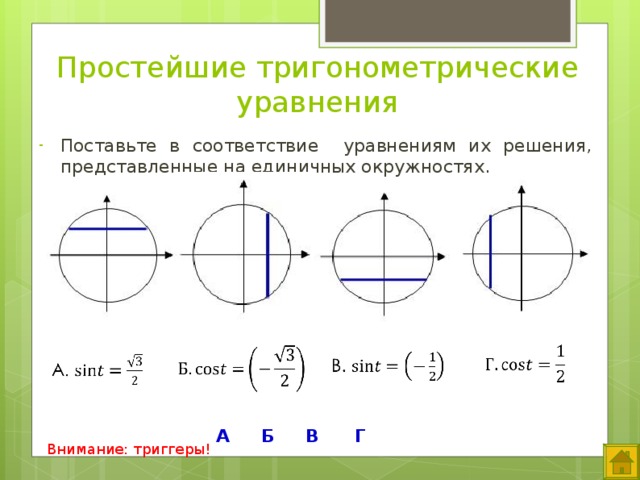
Урок математики в 11 классе по теме:

«Решения тригонометрических уравнений».

(УМС авторов С.М. Никольского и др.)

Авторы: Юрко Олеся Александровна, Юрко Оксана Александровна, учителя математики МОУ СОШ №12 г. Балашова Саратовской области.

Цели и задачи урока.

Образовательные:

- повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения

- сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к квадратным.

- уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к квадратным и решать их.

Развивающие:

- развивать логическое мышление учащихся, память, внимание, речь; умения рассуждать и выделять главное; умение самостоятельно приобретать знания и применять их на практике, развивать навыки самоконтроля и взаимоконтроля.

Воспитательные:

- воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.

Оборудование:

- мультимедийный проектор, экран, лист самооценки.

Организационные формы общения: фронтальная, групповая, индивидуальная.

Тип урока: усвоения новых знаний.

Образовательные технологии: ИКТ, проектная.

План урока.

Из дома реальности легко забрести в лес математики,

но лишь немногие способны вернуться обратно.

Х. Штейнхаус

1. Организационный момент, формирование мотивации работы учащихся.

2. Формулирование темы, цели урока.

3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала.

4. Этап усвоения новых знаний и способов действий.

5. Этап активной релаксации и активизации.

6. Этап первичной проверки понимания изученного.

7. Этап рефлексии и оценивания. Подведение итогов урока.

8. Этап информирования учащихся о домашнем задании, инструктаж по его выполнению.

Ход урока.

Подготовительная работа.

Учащихся класса необходимо заранее поделить на группы. Принцип деления учащихся на группы учитель вправе выбрать самостоятельно.

Один из вариантов - группы, в которые вошли бы учащиеся с разным уровнем математической подготовки: от «базового» до «продвинутого».

Каждая группа предварительно получает задание изучить алгоритм решения одного из типов тригонометрических уравнений (используются предложенные учителем источники информации и самостоятельно найденные). Результаты своей работы члены каждой группы представляют на одном из уроков по теме «Тригонометрические уравнения». В зависимости от объёма предлагаемого материала и его сложности одном уроке могут успеть выступить 1-2 группы, представив результаты своей работы.

Предлагаем вашему вниманию урок, на котором рассматривается решение тригонометрических уравнений, сводящихся к квадратным.

1. Организационный момент, формирование мотивации работы учащихся (3 мин.).

Чем больше человек будет становиться человеком,

тем меньше он согласится на что-либо иное,

кроме бесконечного и неистребимого движения к новому.

Пьер Шарден

Приветствие. Фиксация отсутствующих, проверка готовности учащихся к уроку. Далее каждому ученику выдаётся оценочный лист. Учитель кратко комментирует правила заполнения оценочного листа и предлагает заполнить 1-3 строки. (Приложение 1)

Организация внимания учащихся: учитель цитирует учащимся Пьера Шардена, предлагает пояснить, как они поняли смысл слов (можно выслушать 2-3 человека), предлагает сделать слова девизом урока и интересуется, знают ли они, кто является их автором. Краткая историческая справка (Презентация. Слайд 3).

*Инструкция по использованию Презентации – Приложение 2.

1. Формулирование темы, цели урока (2 - 3 мин.).

Учитель просит сформулировать тему предыдущего урока (Решение простейших тригонометрических уравнений). Интересуется у учащихся, как они думают, существуют ли другие типы тригонометрических уравнений? (Да. Если есть «простейшие», то значит, есть более сложные, иначе нет необходимости вводить термин «простейшие», если это единственный тип тригонометрических уравнений). Исходя из выше сказанного, предлагает сформулировать тему сегодняшнего урока (Решение сложных/других/различных типов тригонометрических уравнений).

После корректировки темы, предлагает учащимся записать в их тетрадях: дату проведения урока, фразу «Классная работа» и тему урока «Решение различных типов тригонометрических уравнений: уравнения, сводящиеся к квадратным».

На столе у каждого из учащихся находятся шаблоны яблок и фломастеры. Предлагается написать на «яблоках» свои ожидания от предстоящего урока, тему которого уже сформулировали. После этого все шаблоны яблок прикрепляются, например, с помощью скотча на заранее приготовленный плакат с изображением дерева. Получается «Дерево ожиданий». По мере достижения того или иного ожидания соответствующее яблоко можно считать созревшим и собирать в корзину. Использование этого активного метода обучения – наглядный способ отслеживания продвижения учащихся на уроке. [1]

Возможен другой вариант: учитель ставит песочные часы перед учениками класса и предлагает ответить на вопрос о том, чему они хотят научиться на уроке, тема которого уже сформулирована (достаточно 1-2 варианта).

1. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала (10 мин.).

Учитель.

Герберт Спенсер говорил, что если знания человека в беспорядочном состоянии, то чем больше их у него, тем сильнее расстраивается его мышление. Последуем совету этого известного британского философа (информация для общего развития личности – краткая историческая справка. (Презентация. Слайд 5) Прежде чем перейти к изучению нового материала, давайте вспомним, что мы знаем из раздела «Тригонометрия».

Фронтальная работа (устно). (Презентация. Слайды 6 - 10).

- При каких значениях а имеют смысл выражения: arcsin a; arccos a; arctg a; arcctg a?

- Продолжите запись: _; _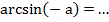

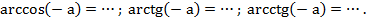- Вычислите: _, _ , _{   }, _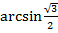

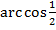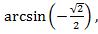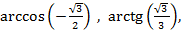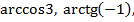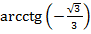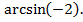- Дайте определение тригонометрического уравнения.

- Сколько корней может иметь тригонометрическое уравнение?

- Что такое простейшие тригонометрические уравнения?

- Что значит решить простейшее тригонометрическое уравнение?

- Какие способы решения тригонометрических уравнений вы знаете? (2 варианта: формулы; единичная окружность).

а) Заполните таблицу:

а	sin x = a	cos x = a
0	х = к	х =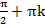 
1	x = 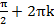	х =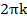
-1	х = - 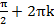	х =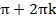 

а	sin x = a	cos x = a
0
1
-1

б). Поставьте в соответствие уравнениям их решения, представленные на единичных окружностях (с комментарием).

Самостоятельная работа. Приложение 3.

С последующей взаимопроверкой/самопроверкой (правильность ответов проверяется с помощью презентации) на умение решать простейшие тригонометрические уравнения. Демонстрируется (Презентация. Слайд 11 - 12). При необходимости решения некоторых уравнений коротко комментируются. Заполняется пункт №4 Приложения 1.

1. Этап усвоения новых знаний и способов действий (15 мин.).

Учащиеся класса предварительно были поделены на группы, каждая из которых самостоятельно рассмотрела, используя материал рекомендуемый учителем и найденный самостоятельно, один из типов тригонометрических уравнений.

Результаты работы оформляются в виде некой рекомендации/алгоритма/схемы решения в формате презентации Power Point. Учитель в случае необходимости консультирует учащихся групп и предварительно проверяет итоговый продукт их работы.

Для презентации результатов того или иного способа решения на уроке выбирается один из представителей группы, остальные на уроке помогают отвечать на возникающие вопросы по решению данного типа тригонометрического уравнения. Учащиеся заранее знакомятся с критериями оценивания своей работы в группе.

Мне приходится делить время

между политикой и уравнениями.

Однако уравнения, по-моему, гораздо важней.

Политика существует только для данного момента,

а уравнения будут существовать вечно.

Альберт Эйнштейн

Возможные варианты выполнения задания группой. (Презентация. Слайды 14-18)

1 группа. Решение тригонометрических уравнений, сводящихся к  квадратным.

Отличительные признаки уравнений, сводящихся к квадратным:

1. В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.

2. В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.

Алгоритм решения:

- Используются ниже приведённые тождества; с их помощью необходимо выразить одну тригонометрическую функцию через другую:
sin² x + cos² x = 1;
tg²x + 1 = 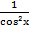_, где x ≠ _ + πn, n є Z;
ctg²x + 1 = 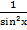_, где x ≠ πk, k є Z.   

- Выполняется подстановка.

- Выполняется преобразование выражения.

- Вводится обозначение (например, sinx = y).

- Решается квадратное уравнение.

- Подставляется значение обозначенной величины, и решается тригонометрическое уравнение.

Пример №1
6cos² x + 5 sin x - 7 = 0.

Решение.
1) Используя тождество sin² x + cos² x = 1 , осуществим замену cos² x = 1- sin² x:
6 (1- sin² x) + 5 sin x -7 = 0;
6 - 6sin² x + 5 sin x -7 = 0;
- 6sin² x + 5 sin x – 1 = 0|·(- 1);
6sin² x - 5 sin x + 1 = 0;
2) Обозначение: t = sin x, где -1 ≤ t ≤ 1.
6t² - 5t + 1 = 0;
D = (-5)² - 4·6·1 = 25 - 24 = 1;
t₁=_= _;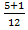
t₂ =_= _;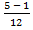
3) -1≤ t₁ ≤1, подходит; -1≤ t₂≤1, подходит;
4) Вернёмся к обозначению:
а) sin x = _;
x = (-1)ⁿ arcsin _ + πn, где n є Z;
х = (-1)ⁿ 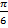_ + πn, где n є Z;
б) sin x = _;
x = (-1)^m arcsin_ + πm, где m є Z.
Ответ: (-1)ⁿ 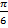_ + πn, где n є Z; (-1)^m arcsin_ + πm, где m є Z.

Пример 2

2cos ² 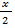 _౼ 5sin _ ౼ 5 = 0.

Решение.

1) 2·(1 ౼ sin ²_) ౼ 5 sin_ ౼ 5 = 0;
 2sin ² _ + 5sin_ + 3 = 0;

2) Обозначение: sin _ = t,  -1 ≤ t ≤ 1.
2t ² + 5t + 3 = 0
t ₁ = -1, удовлетворяет условию -1 ≤ t ≤ 1.

t ₂ = - 1,5 - не удовлетворяет условию -1 ≤ t ≤ 1.

3) Вернёмся к обозначению:

sin _ = 1,

_= _ + 2 πn, n ∊ Z

 x = π + 4πn, n ∊ Z
Ответ: π + 4πn, n ∊ Z.

Пример №3
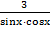_ + _ – 4 = 0.

Решение.
1) Обозначение: _ = t;
t² + 3t – 4 = 0;
D = 3² - 4·1·(- 4) = 9 + 16 = 25;
t₁= 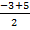_ = 1;
t₂= 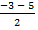_= - 4;
Так как 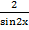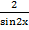_ = _; │_│≥ 2 , то корень t₁ = 1 - не подходит;
2) Вернёмся к обозначению:
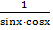_= - 4;

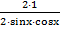_= - 4;

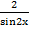_= - 4;

sin2x = - _;
2x = (-1)ⁿ arcsin(- _) + πn, где n є Z;
2х = (-1)ⁿ (-1)_ + πn, где n є Z;
2x = (-1)^ⁿ⁺1 _ + πn|:2 (n є Z);
x = (-1)^ⁿ⁺1 _ + _, где n є Z.
Ответ: (-1)^ⁿ⁺1 · _ + _, где n є Z. Заполняется пункт №5 Приложения 1.

1. Этап активной релаксации и активизации (2 мин.).

Авторы метода: С. Казаков, Ю. Долинова. Приложение 4 (текст). Презентация, слайды 19 - 25.

1. Этап первичной проверки понимания изученного (8 мин.).

Самостоятельная работа. Приложение 5.

Работа дифференцированная, каждый уровень сложности заданий представлен в двух вариантах.

I уровень – «3», II уровень – «4», III уровень – «5» в случае полного правильного решения. Работа будет проверена учителем к следующему уроку, отметки будут выставлены за урок.

1. Этап рефлексии и оценивания. Подведение итогов урока (2 мин.).

Заполнить пункт №6,7 листа самооценки - Приложение 1.

1. Этап информирования учащихся о домашнем задании, инструктаж по его выполнению (2 мин.).

Дифференцированное (раздаётся каждому ученику на отдельных листах) - Приложение 6.

Список литературы.

1. Корнилов С.В., Корнилова Л.Э. Методический ларец. - Петрозаводск: ПетроПресс, 2002. - 12 с.

Ниже представлены Приложения (№1 - 6).

Приложение 1

Лист самооценки.

1

Дата:

Фамилия:

2

Класс:

Имя:

3

Настрой на работу - начало урока

4

Самостоятельная работа «Простейшие тригонометрические уравнения»

Решил все уравнения

Решил пять уравнений

Решил четыре уравнения

Решил три уравнения

Решил два уравнения

Решил одно уравнение

Не решил ни одного уравнения

5

Новая тема

Тригонометрические уравнения, сводящиеся к квадратным

Понятно, как отличить от других

Понятно как решать

Понятно и как отличить, и как решать

Ничего не понял

6

Самостоятельная работа

Выбрал_______ уровень, ______вариант

7

Итог

Я научился… 1. 2. 3.

Я могу научить других…. 1. 2. 3.

Я не понял… 1. 2. 3.

В дальнейшем я собираюсь… 1. 2. 3.

Приложение 2

Слайды презентации расположены в том порядке, в котором их необходимо использовать при проведении урока.

Для удобства дополнительно создана навигация. На каждом слайде в правом нижнем углу есть «домик», нажав на который можно попасть на слайд с содержанием, а далее по ссылке на нужный слайд. Кроме того, переход от слайда к слайду осуществляется по щелчку левой клавишей «мышки», кроме тех слайдов, на которых размещаются триггеры (специальная пометка: Внимание: триггеры!).

На слайдах с триггерами для перехода на другой слайд надо поступить так: нажать на «домик», расположенный в правом нижнем углу – перейдёте на слайд с содержанием, а далее по ссылке на нужный слайд.

В заметках к слайдам также есть полезная информация, с ней желательно познакомиться до момента запуска презентации.

Приложение 3

Этап. Актуализация знаний и подготовки учащихся к активному и сознательному усвоению нового материала.

Самостоятельная работа.

1 вариант		2 вариант
	t =  t =  	  	t =  t = 7

Приложение 4

Этап активной релаксации и активизации.

Авторы метода: С. Казаков, Ю. Долинова.

Текст, сопровождающий слайды Презентации (зачитывается учителем, когда учащиеся просматривают слады)

- Сядьте поудобнее, закройте глаза. Сделайте несколько глубоких вздохов. Вы уже взрослые, а иногда так хочется побыть ребёнком. Давайте не будем отказывать себе в этом желании и на мгновение вернёмся в мир детства! Итак, представьте, что вам 5 лет.

- Почувствуйте себя ребёнком, который построил крепость из песка…(Слайд 20)

- Почувствуйте себя ребёнком, который в восторге от мыльных пузырей… (Слайд 21)

- Почувствуйте себя ребёнком, который впервые увидел распускающийся цветок… (Слайд 22)

- Почувствуйте себя ребёнком, которому на день рождения подарили огромное количество подарков… (Слайд 23)

- Почувствуйте себя ребёнком, который путешествует с родителями и любуется прекрасными пейзажами… (Слайд 24)

- Почувствуйте себя ребёнком, которому родители купили много-много воздушных шариков. И он идёт с ними по улице. Прекрасный солнечный день и много-много воздушных шариков… (Слайд 25)

Приложение 5

Этап первичной проверки понимания изученного.

Самостоятельная работа.

I уровень

1 вариант

sin² x – _sinx = 0

2 вариант

cos2 x + _cosx =0

II уровень

1 вариант

3sin² x – cosx – 3 = 0

2 вариант

5 sin² x – cosx – 5 = 0

III уровень

1 вариант

sin² x + 4cosx – 3 = 0

2 вариант

8sin² x + cosx + 1 = 0

Приложение 6

Этап информирования учащихся о домашнем задании, инструктаж по его выполнению.

Дифференцированное (раздаётся каждому ученику на отдельных листах):

1 уровень («3»): 2cos² x + 3cosx + 1 = 0; 2_x - 7sin(_) - 5 = 0.

2 уровень («4»): 3 + cos2x + 3_ cosx = 0; 2cos2x - 3 _x - 2sin x = 0.

3 уровень («5»): cos(2π - 2x) + 3sin(π - x) = 2; _(_;

6_ sin(π – 2x) - _.

2 группа готовится по теме «Тригонометрические уравнения, решаемые на основе формул сложения».

Всероссийском педагогическом конкурсе «Сценарий медиаурока с компьютером»

Тригонометрические уравнения

Авторы: Юрко Олеся Александровна,

Юрко Оксана Александровна,

учителя математики МОУ СОШ №12

г. Балашова Саратовской области.

2013-2014

Содержание

Пьер Шарден

Дерево ожиданий

Герберт Спенсер

Вспомним главное:

Отличительные черты уравнений

Алгоритм решения

Пример 1

Пример 2

Пример 3

Релаксация

Самостоятельная работа №2

Рефлексия

Домашнее задание

• смысл выражений,
• вычислите,
• продолжите запись,
• заполните таблицу,
• соотнесите.

Самостоятельная работа №1

Ответы

Исаак Ньютон

Чем больше человек будет становиться человеком,

тем меньше он согласится

на что-либо иное,

кроме бесконечного и неистребимого движения

к новому.

Пьер Шарден

(1881-1955)

http://ru.wikipedia.org/wiki/%D2%E5%E9%FF%F0_%E4%E5_%D8%E0%F0%E4%E5%ED,_%CF%FC%E5%F0

Французский геолог, палеонтолог, философ, священник-иезуит. Создал своего рода синтез католической христианской традиции и современной теории космической эволюции.

Для возврата на страницу с содержанием, необходимо нажать на «домик».

Википедия

Энциклопедия Кольера

УГТУ

Афоризм.ру

Дерево ожиданий

Тригонометрические уравнения,

сводящиеся к квадратным.

Хочу узнать:

1

• Как отличить от других?
• Как решать?
• Кто придумал алгоритм решения?
• Сколько корней может быть?

4

2

3

При нажатии на яблоко выходит фраза, которая соответствует одному из ожиданий учащихся от урока. Сначала познакомиться с вариантами ожиданий учащихся, затем вернуться на слайд с содержанием (нажать на «домик»)

Внимание: триггеры!

http://office.microsoft.com

Если знания человека в беспорядочном состоянии, то чем больше их у него, тем сильнее расстраивается его мышление.

Герберт Спенсер

Википедия

БСЭ

Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

(1820 —1903)

http://ru.wikipedia.org/wiki/%D1%EF%E5%ED%F1%E5%F0,_%C3%E5%F0%E1%E5%F0%F2

Английский философ и социолог, один из родоначальников позитивизма .

Вспомним главное…

- При каких значениях а имеют смысл выражения:

-1 ≤ а ≤ 1

arcsin a;

-1 ≤ а ≤ 1

arc с os a;

а - любое

arctg a;

arcctg a?

а - любое

Для проверки правильности ответов, необходимо щёлкнуть (предварительно подведя курсор) левой клавишей мышки на соответствующее выражение, например, чтобы узнать значение а, при которых имеет смысл выражение arcsin a, надо нажать на arcsin a.

Внимание: триггеры!

Вспомним главное…

- Вычислите:

- не существует

Выход элементов по «щелчку».

- не существует

Вспомним главное…

- Продолжите запись:

• Дайте определение тригонометрического уравнения.
• Сколько корней может иметь тригонометрическое уравнение?
• Что такое простейшие тригонометрические уравнения?

- Что значит, решить простейшее тригонометрическое уравнение?

Выход элементов по «щелчку».

Простейшие тригонометрические уравнения

 

 

 

π k

sin x = 0

cos x = 0

sin x = 1

cos x = 1

sin x = - 1

cos x = - 1

Для проверки правильности ответов, необходимо щёлкнуть левой клавишей мыши (предварительно подведя курсор) по соответствующей записи. Например, чтобы проверить правильность формулы корней уравнения sin x = 0, надо нажать на запись sin x = 0.

Внимание: триггеры!

Простейшие тригонометрические уравнения

• Поставьте в соответствие уравнениям их решения, представленные на единичных окружностях.

Чтобы увидеть правильный ответ, необходимо нажать левой клавишей мыши(предварительно подведя курсор) на соответствующий рисунок, выйдет буква, под которой записан правильный ответ.

Б

В

Г

А

Внимание: триггеры!

Самостоятельная работа

1 вариант

2 вариант

Самостоятельная работа. Ответы.

π k

Нет решений

Нет решений

Выход элементов по «щелчку».

а rctg7 + π n , где n є Z

Мне приходится делить время

между политикой и уравнениями.

Однако уравнения, по-моему, гораздо важней.

Политика существует только для данного момента,

а уравнения будут существовать вечно.

Альберт Эйнштейн

(1879 — 1955)

http://ru.wikipedia.org/wiki/%DD%E9%ED%F8%F2%E5%E9%ED,_%C0%EB%FC%E1%E5%F0%F2

Физик-теоретик, один из создателей современной физики.

Википедия

Энциклопедия «Вокруг света»

Koob.ru

Тригонометрические уравнения, сводящиеся к  квадратным.

Отличительные признаки таких уравнений:

• В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.
• В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.

6 sin ² x + 5 cos2 x - 7 = 0

Выход элементов по «щелчку».

6cos² x + 5 sin x -7 = 0

6 sin ² x + 5 sin x - 7 = 0

Алгоритм решения

• Используются ниже приведённые тождества:

• Необходимо выразить одну тригонометрическую функцию через другую.

• Вводится обозначение (например, sin x = y ).

• Решается полученное квадратное уравнение.

- Подставляется значение обозначенной величины, и решается тригонометрическое уравнение.

Выход элементов по «щелчку».

Пример №1

6cos² x + 5 sin x - 7 = 0.

sin² x + cos² x = 1

cos² x = 1- sin² x

6 (1- sin² x) + 5 sin x - 7 = 0;

6 - 6sin² x + 5 sin x - 7 = 0;

- 6sin² x + 5 sin x – 1 = 0|·(- 1);

6sin² x - 5 sin x + 1 = 0;

Обозначение: t = sin x, где -1 ≤ t ≤ 1.

6t² - 5t + 1 = 0;

D = (-5)² - 4· 6·1= 25 -24 =1;

Выход элементов по «щелчку».

Пример №2

t ² + 3 t – 4 = 0;

D = 3² - 4·1· (- 4) = 9 + 16 = 25;

t ₁ = 1 – не подходит.

Вернёмся к обозначению:

Выход элементов по «щелчку».

Пример № 3

t 1 = -1, t 2 = − 1,5 - не удовлетворяет условию (*).

2t 2 + 5t + 3 = 0;

Вернёмся к обозначению:

Выход элементов по «щелчку».

x = π + 4π n , n ∊ Z

Ответ: π + 4π n , n ∊ Z .

Релаксация.

Авторы метода: Казаков С., Долинова Ю.

- Сядьте поудобней закройте глаза.

- Сделайте несколько глубоких вздохов.

Вы уже взрослые, а иногда так хочется побыть ребёнком.

Давайте не будем отказывать себе в этом желании и на мгновение вернёмся в мир детства!

Итак, представьте, что вам 5 лет.

Слайды №20-25 сопровождаются текстом, который зачитывает учитель (Приложение №4).

Самостоятельная работа. Ответы

III уровень

 

1 вариант

sin 2 x +4cos x – 3 = 0

 

2 вариант

8sin 2 x + cos x + 1 = 0

Этап рефлексии и оценивания.

Я научился…

1.

2.

3.

Я могу научить других….

1.

2.

3.

Я не понял…

1.

2.

3.

В дальнейшем я собираюсь…

1.

2.

3.

Домашнее задание

Использованные источники информации

• Международный Институт Развития ЭкоПро. Электронная книга «Копилочка активных методов обучения».
• http://office.microsoft.com/ru-ru/images (фото на слайдах №20-25, рис. на слайде №4, рис. 3-5 в Приложении1).