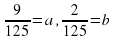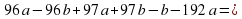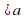Некоторые эвристические приемы решения задач
(методическая разработка урока)
Тема: «Некоторые эвристические приемы решения задач»
Цели урока:
- предметные: рассмотреть некоторые эвристические приемы решения задач, познакомить с методами и приемами решения олимпиадных задач;
- метапредметные: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание, формировать понятие площади;
- личностные: развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.
Тип урока: комбинированный.
Методы: по источникам знаний: словесные, наглядные, практический.
Формы работы: фронтальная, работа в парах, индивидуальная
Оборудование: тетради, ручки, ноутбук или проектор для просмотра презентации.
Некоторые эвристические приемы решения задач
введение вспомогательной неизвестной
крайних случаев рассмотрение
контрольный и подтверждающий пример
перебор
перефразирование
прием получения следствий
Ход урока.
Организационные моменты.
Знакомство детей. Игра «Снежный ком».
Деление на 3 группы.
Изучение нового материала
Введение вспомогательной неизвестной
Задача 1
Вычислить наиболее удобным способом
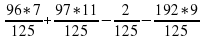

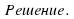 Введем вспомогательную переменную (замена)
Введем вспомогательную переменную (замена)
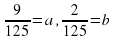

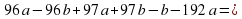
Ответ: 9/125.
Задача 2
Вычислить: 2379 × 23782378 – 2378 × 23792379
Решение.
Выполним замену 2378 = х.
2379 = х + 1,
23782378 = 10000 х + х,
23792379 = 10000 (х + 1) + х + 1
(x+1)*(10000x+x)-x* (10000 (х + 1) + х + 1)
Ответ: 0
Перебор
Задача 1
Сколько имеется двузначных чисел, у которых а) среди цифр есть хоть одна пятерка? б) цифра десятков меньше цифры единиц? в) цифра десятков больше цифры единиц?
Ответ: а) 18; б) 36; в) 45
Задача 2
Среди трехзначных чисел, выражающих количество изделий, изготовленных каждой из соревнующихся бригад, нет одинаковых, но в каждом из них сумма цифр равна 4. Какое наибольшее число бригад могло быть? Сколько изделий изготовила каждая из них?
Решение
Всего имеется 10 чисел, удовлетворяющих условию: 400, 301, 310, 130, 103, 202, 220, 211, 121, 112, по этому наибольшее число бригад 10.
Ответ: 10.
Задача 3
Для нумерации страниц книги потребовалось всего 1 392 цифры. Сколько страниц в этой книге?
Решение.
На нумерацию страниц 1–9 идет по одной цифре, страниц 10-99 – по две цифры, страниц 100-500 – по три цифры, причем 1 × 9 + 2 × 90 + 3 × 401 = 1392. Значит, в книге 9 + 90 + 401 = 500 страниц.
Ответ: 500 страниц.
Крайних случаев рассмотрение
Задача 1
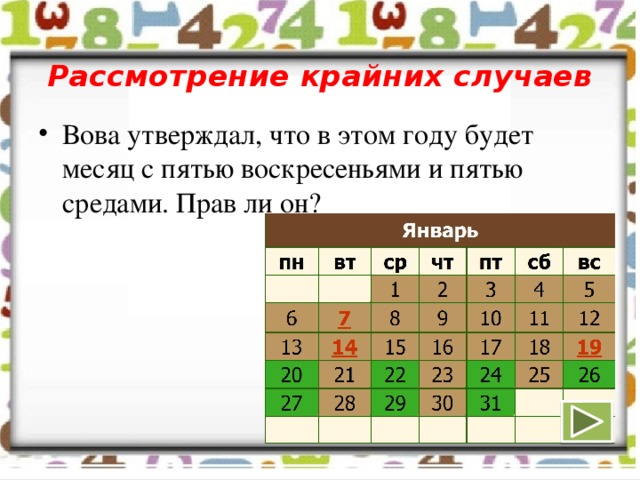
Вова утверждал, что в этом году будет месяц с пятью воскресеньями и пятью средами. Прав ли он?
Решение
Рассмотрим самый благоприятный, случай в месяце 31 день. Так как 31 = 4 × 7 + 3 и среди трех идущих подряд дней недели не могут быть и воскресенье, и среда, а лишь один из этих дней, то в этом месяце может быть либо 5 воскресений и 4 среды, либо 4 воскресения и 5 сред. Следовательно, Вова не прав.
Задача 2
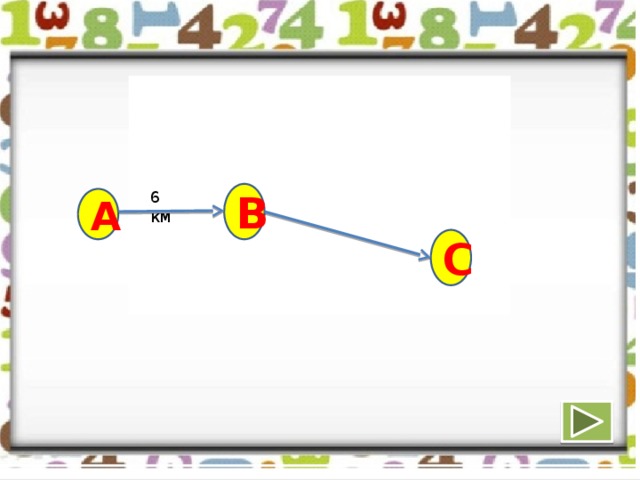
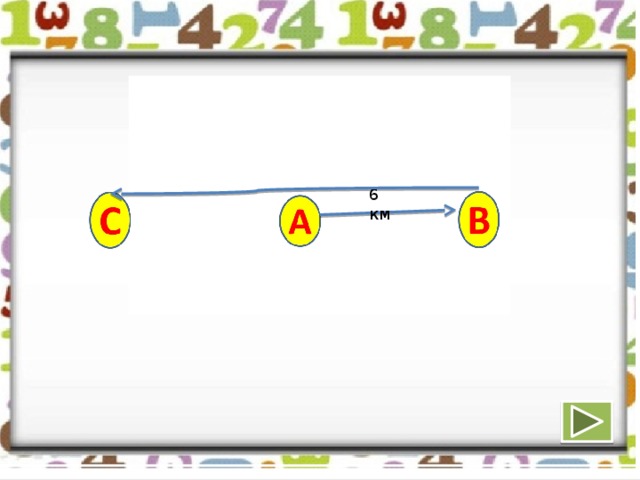
Расстояние от пункта А до пункта В 6 км, а от пункта В до пункта С вдвое больше. Может ли расстояние между пунктами А и С быть а) 19 км? б) 6 км? в) 10 км? г) 4 км?
Решение
Наибольшее расстояние, которое может быть между А и С, равно 18 км (в этом случае пункт А расположен между пунктами В и С). Значит, все возможные значения расстояния расположены в пределах от 6 до 18 км.
Ответ: а) нет; б) да; в) да; г) нет
Контрольный и подтверждающий пример
Задача 1
Верно ли, что если произведение двух натуральных чисел больше 100, то каждое число больше 10?
Ответ: Нет. Например: 8 × 13 = 104 100, но 8
Задача 2
Можно ли число 45 представить в виде суммы нескольких натуральных чисел так, чтобы произведение всех этих чисел тоже было равно 45?
Ответ: Да, можно. Например: 45 = 15 + 3 + 1 + 1 + … + 1 = 15 × 3 × 1 × 1 × … × 1. 27 единиц
Задача 3
Может ли произведение двух дробных чисел быть целым числом?
Ответ: Да. Например: 3/4 * 8/3 = 2.
Перефразирование
Задача 1
За кухонный гарнитур заплатили сначала 41600 рублей, а затем еще половину стоимости этого гарнитура. Сколько стоит кухонный гарнитур?
Решение.
Перефразируем задачу так: «Какова стоимость кухонного гарнитура, если ее половина равна 41600 рублей?»
Ответ: 83200 рублей.
Задача 2
Один из двух множителей равен 12. Как изменится произведение, если второй множитель увеличить на 5?
Решение.
Перефразируем задачу так: «Что больше и на сколько 12а или 12*(а+5)?»
Ответ: увеличится на 60.
Задача 3
Ученики одного класса в течении 7 месяцев собирали деньги для поездки на экскурсию. Было собрано 640 р. 1 к. Сколько учеников было в классе и сколько каждый вносил ежемесячно, если эти взносы были одинаковыми?
Решение
Так как каждый месяц учащиеся вносили 64 001 : 7 = 9 143 коп, то число 9 143 является произведением числа учеников класса на ежемесячный взнос. Существуют лишь две возможности представления числа 9 143 в виде произведения натуральных чисел: 9 143 = 9 143 × 1 и 9 143 = 223 × 41. Исходя из условия задачи, получаем, что в классе 41 ученик и каждый вносил ежемесячно 2 р. 23 к.
Прием получения следствий
Задача 1
Сколько всего прапрабабушек и прапрадедушек было у всех Ваших прапрабабушек и прапрадедушек?
Решение
Так как у каждого человека было 8 прапрабабушек и 8 прапрадедушек, а у каждого из этих 16 человек так же было по 16 прямых предков в «четвертом колене», то искомое число равно
16 × 16 = 256.
Ответ: 256.
Задача 2
Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равны делимое, делитель и частное?
Решение
Делимое в 6 раз больше делителя означает, что частное равно 6. Отсюда, если частное равно 6, а делитель в 6 раз больше частного, то делитель равен 36. Окончательно получаем, что делимое равно 36 × 6 = 216.
Ответ: 216.
Задача 3
Жили дед и баба. Была у них курочка Ряба. Курочка несет каждое второе яичко простое, а каждое третье – золотое. Может ли такое быть?
Ответ: нет. Шестое яичко будет и вторым, и третьим, так как 6 : 2 и 6 : 3.
Самостоятельная работа по группам. (7 мин)
Задача 1
В числе 48352 зачеркните такие две цифры, чтобы число, образованное оставшимися цифрами в том же порядке, было а) наибольшим, б) наименьшим.
Ответ: а) 852 б) 352.
Задача 2
Можно ли представить единицу в виде суммы шести дробей с числителем, равным 1, и различными нечетными знаменателями? Ответ: нет.
Задача 3
Семь рыбаков ловили рыбу на озере. Первый рыбачил каждый день, второй – через день, третий – через 2 дня и т.д., седьмой – через 6 дней. Сегодня все рыбаки на озере. Через сколько дней все 7 рыбаков снова соберутся вместе на озере?
Ответ: 420 дней.
Задача 4
Половина – треть некоторого числа. Какое это число?
Решение.
Если треть числа – это 1/2, то само число равно 3 * 1/2 = 3/2.
Ответ: 3/2.
Подведение итогов. Рефлексия (самооценка).
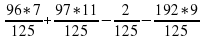

 Введем вспомогательную переменную (замена)
Введем вспомогательную переменную (замена)