Тема урока: Теорема о трёх перпендикулярах, её применение при
решении задач.
Цели урока:
обучающие:
закрепить изученный теоретический материал на практике, обосновать необходимость теоремы о трех перпендикулярах;
сформировать видение изученной закономерности в различных ситуациях: при решении задач на доказательство или задач, требующих найти численное (буквенное) значение, какого – либо элемента;
учить умению читать чертеж;
учить умению объяснять, комментировать выполняемое упражнение в виде цельного связного рассказа;
учить решать задачи, встречающиеся на ГИА;
развивающие:
способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания;
развивать навыки исследовательской деятельности (выдвижение гипотез, анализ и обобщение полученных результатов);
развивать умение определять цели урока;
развивать умения самостоятельно контролировать своё время;
воспитательные:
развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, элементы ораторского искусства);
способствовать развитию творческой деятельности учащихся, потребности к самообразованию;
развивать ИКТ-компетентности;
воспитывать патриотическое отношение к родному краю.
Тип урока: урок обобщения и систематизации знаний.
Класс:10.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Оборудование: плакат с эпиграфом урока,мультимедийная установка, компьютеры с выводом в интернет; учебник:Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. «Геометрия 10-11 класс: учеб. для общеобразовательных организаций: базовый и углубленный уровень». – М.: Просвещение, 2016, раздаточный материал.
Интернет-ресурсы: http://www.yaklass.ru/ https://ru.wikipedia.org/wiki
Програмное обеспечение: MS Exel, MS Power Point, Flash Plaer NetOp School (для трансляции изображения с монитора учителя на все мониторы учеников и на экран проектора).
Геометрия-учитель точности,
готовит наш ум к глубоким
исследованиям природы.
Т.В.Осиповский.
Главное значение перпендикуляра –
это его роль в технике
и во всём нашем обиходе.
О.Д. Александров.
Ход урока
| № | Етап урока | Вид деятельности | Время (мин) |
| І | Организационный момент | Заповлнение таблицы «Цели урока» | 2 |
| ІІ | Проверка домашнего задания | Теоретический опрос. Интелектуальная разминка. (Онлайн‒тренажёр) Заполнение пропусков в задаче у доски | 6 |
| ІІІ | Актуализация опорных знаний | Работа в парах (заполнить таблицу) | 6 |
| ІV | Обобщение и систематизация знаний учащихся по теме
| Найди ошибку(подготовка к ГИА) | 4 |
|
|
| Математическое лото | 6 |
|
|
| Физкультминутка для глаз | 1 |
|
|
| Решение прикладной задачи(подготовка к ГИА) | 7 |
|
|
| Самостоятельная работа (онлайн‒тестирование) | 8 |
| V | Итог урока | Рефлексия | 3 |
| VI | Домашнее завдання | Дифференцированное | 2 |
І. Организационный момент
1.Учитель оглашает тему, эпграф урока.(Слайд2,3)
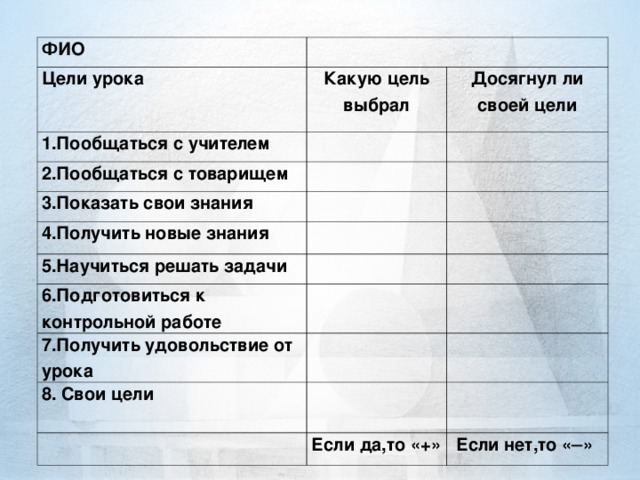
2.Учитель раздаёт учащимся (Приложение 1), с помощью которых они вместе с учителем ставят перед собой цели урока. В течении урока учащиеся обращаются к ней дважды‒в начале и в конце, во время подведения итогов.(Слайд4,5)
3.Учитель инструктирует учащихся по карточкам самоконтроля, которые оформлены в текстовом редакторе EXEL (Приложение 2).С помощью формул нахождения среднего значения в EXEL в конце урока учащиеся самомтоятельно посчитаю свой средний балл(каждое задание оценвается по 5 бальной системе).После чего отправят результаты на ПК учител
ІІ. Проверка домашнего задания и актуализация опорных знаний
Один ученик работает у доски и заполняет пропуски в решении домашней задачи, вэто время проводится интеллектуальная разминка.
Индивидуальная работа у доски
Заполнить пропуски
Задача 1.Из вершины A квадрата АВСD проведен перпендикуляр KA к его плоскости. Найдите расстояние CK, если KA равно 6 см, а сторона квадрата - 4�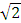 � см.
� см.
Решение
П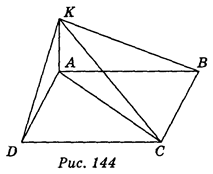 роведём диагональ АС квадрата АВСD. ∆АСK – прямоугольгый, поскольку KA�
роведём диагональ АС квадрата АВСD. ∆АСK – прямоугольгый, поскольку KA�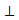 �АС по определению перпендикулярности прямой и плоскости.
�АС по определению перпендикулярности прямой и плоскости.
По данной стороне квадрата находим его диагональ:
АС = АD�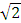 � = 4∙�
� = 4∙�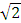 �∙�
�∙�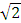 � = 8 см.
� = 8 см.
З ∆АСK по теореме Пифагора имеем:
CK = � � см.
� см.
Ответ:CK= 10 см.
Теоретический опрос.
Интелектуальная разминка (Слайд6)
Учащиеся переходят по ссылке http://www.yaklass.ru/ и выполнят задания онлайн‒тренажёра,озвучивая свои ответы вслух.
ІІІ. Закрепление и применение знаний
Работа в парах(Слайд 7)
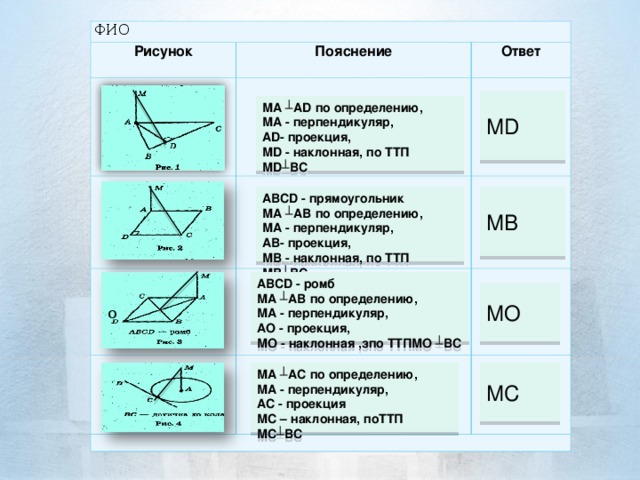
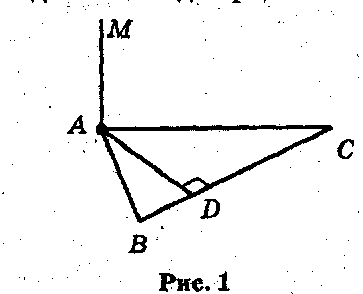
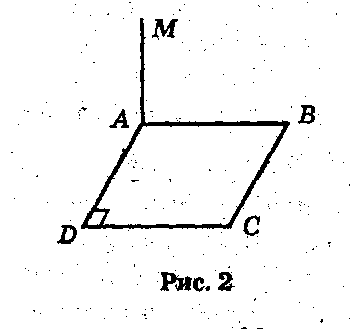
На рисунках 1-4 МА┴(АВС). По рисункам обоснуйте расстояние от точки М до прямой ВС. Учащиеся получают карточки с рисунками и таблицей , которую необходимо заполнить(Додаток 3)
После выполнения учащиеся сверяют свои ответы с таблицей на экране проэктора.
2.Найди ошибку(Слайд 8)
На экране проектора появляется решение задачи ГИА 2015. Учащиеся должны найи ошибку.
Д
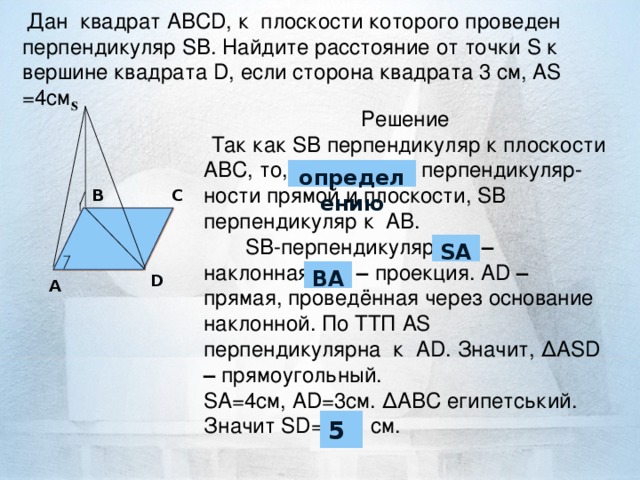
 ан квадрат ABCD, к плоскости которого проведен перпендикуляр SB. Найдите расстояние от точки S к вершине квадрата D, если сторона квадрата 3 см, AS =4cм S
ан квадрат ABCD, к плоскости которого проведен перпендикуляр SB. Найдите расстояние от точки S к вершине квадрата D, если сторона квадрата 3 см, AS =4cм S
 В С
В С




А D
Решение
Так как SB перпендикуляр к плоскости АВС, то, по признаку (определению) перпендикулярности прямой и плоскости, SB перпендикуляр к АВ.
SB-перпендикуляр, AD (АS) – наклонная, ВD (BA) – проекция. АD – прямая, проведённая через основание наклонной. По ТТП AS перпендикулярна к АD. Значит, ∆ ASD – прямоуголный.
SA=4cм, AD=3см. ∆ АВС египетский. Значит SD=7(5)cм.
3. Математическое лото.(Слайд 9)
Учитель предлагает учащимся установить соответствие между задачами и ответами к ним. Задачи-ГИА 2015. (Приложение 4).
| Задачи |
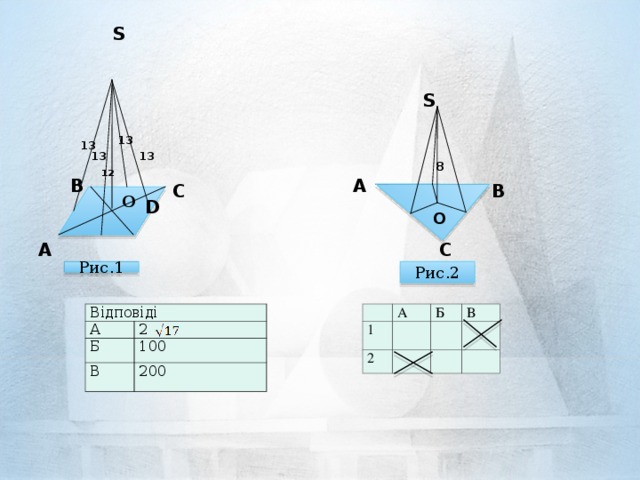
| 1 | Точка удалена от каждой стороны ромба на 13 см, находится на расстоянии12 см от плоскости ромба. Найдите площадь ромба, если его сторона равна 20см. |
| 2 | Р ассояние отточки,равноудалённой от сторон правильного треугольника,до плоскости треугольника равно 8 см. Найдите расстояние от этой точки до сторон треугольника, если его периметр равен 36� ассояние отточки,равноудалённой от сторон правильного треугольника,до плоскости треугольника равно 8 см. Найдите расстояние от этой точки до сторон треугольника, если его периметр равен 36�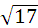 � см. � см. |
Учащиеся сверяют свои ответы (Слайд 10)
| Ответы |
| А | 2 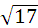 |
| Б | 100 |
| В | 200 |
4.Физкультминутка для глаз
Учащиеся выполняют упражнения для глаз, глядя на экран проектора (Приложение5).
5. Решение задач прикладного содержания
Учитель предлагает учащимся перейти по ссылке https://ru.wikipedia.org/wiki (Слайд 11)и ознакомится с историей возникновения площади имени Ленина в городе Донецке.Учащиеся озакамливаются со статьёй и слушают комментарии учителя.
Памятник Ленину и тригранный пилон были установлены на площади имени Ленина Ворошиловского района города Донецка в 1967 году. Памятный ансамбль из статуи и пилона установлен к годовщине пятидесятилетия Октябрьской революции. Над композицией работали скульптор Кунцевич Е. и архитектори Иванченко В. и Иванченко Н. Бронзовая скульптура Ленина выполнена во весь рост и стоит на високому гранитному пьедестале , висота постамента и скульптуры приблизительно 13,5 метров. Рядом находится 42-метровый пилон, который был изготовлен из тригранных элементов из нержавеючщей стали. Скульптура обращена на юг, где находится металургический завод г. Донецька, который раньше носил імя Владимира Ильича Ленина. В основе пилона гранитные плиты, под которыми замурованы посланния для будущих поколений. Первая капсула содержит послания, которое было подготовлено 29 октября 1971 года участниками встречи трудовых династий, и будет открыто 29 октября 2018 года. Вторая будет открыта ко дню сторлетия Ленина 22 апреля 2020 года, в ней письмо для молодёжи города.
-Возможно, вы будете теми и адрессатами, которые откроют эту капсулу , прочтут послания своих предков и закладёте новую для будущих поколений. Вы – наше будущее, ви наша надежда.
Задача:
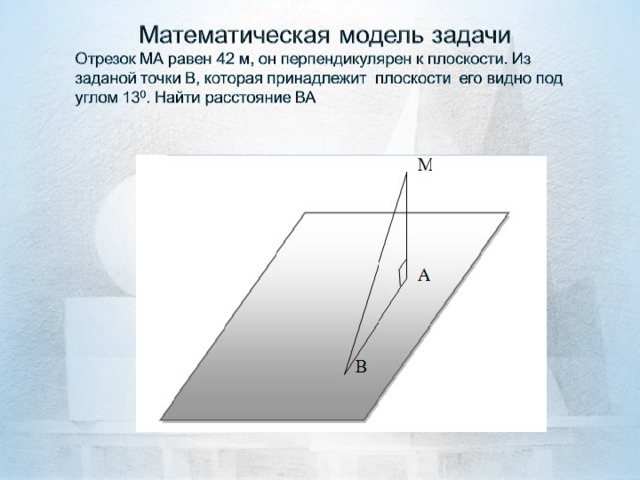
Расчитать расстояние от фонтана до пилона, расположенного на площади им. Ленина, если высота пилона 42 м, а от фонтана його видно под углом 130.

Учитель предлагает учащимся составить математическую модель задачи и решить еёу доски(Слайд 12):
Отрезок МА равен 42 м, он перпендикулярен к плоскости. Из заданой точки В, которая принадлежит плоскости его видно под углом 130. Найти расстояние ВА
M





А

В
6.Самостоятельная работа
Учащиеся переходят по ссылке http://www.yaklass.ru/ и выполняют онлайн-тест по теме урока. Результаты теста автоматически отправляются на почту учителю.О своих оценках дети узнают на следующем уроке.(Слайд 13)
V. Домашнее задание.
Решить №145, №143, №140, повторить п.19,20.
Дополнительная задача:
Через сторону АD ромба ABCD проведена плоскость α. Найдите расстояние от прямой ВС до плоскости α, если S ромба = 80 см2, высота равна 8 см, а угол между проекцией стороны CD и прямой AD равен 45º.
Выполнить тренировочный тест для подготовки к ГИА
http://math-test.ru/
(Слайд 14)
Домашнее задание выдыётся с комментариями учителя.
VІ. Подведение итогов урока. Рефлексия.
1. Заполнение карточек самооценивания и подсчёт среднего балла за урок.
2.Анализ достигнутых результатов по таблице «Цели урока».
9
 ровед
ровед
 ан квадрат
ан квадрат  В С
В С



 ассояние отточки
ассояние отточки










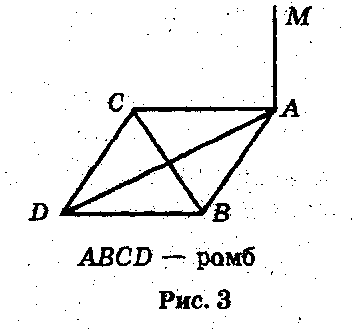

 Рассояние отточки, равноудалённой от сторон правильного треугольника,до плоскости треугольника равно 8 см. Найдите расстояние от этой точки до сторон треугольника, если его периметр равен 36
Рассояние отточки, равноудалённой от сторон правильного треугольника,до плоскости треугольника равно 8 см. Найдите расстояние от этой точки до сторон треугольника, если его периметр равен 36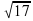 см.
см.