Конспект урока математики,
проведенного в 6 классе учителем 1 квалификационной категории
Туленковой Н.В.
Аннотация: Творческое обучение математике требует индивидуализации, учета психологических различий учащихся. У одной части учащихся имеется устойчивый интерес к математике, у другой - запущенность различного уровня. Ученики одного и того же класса отличаются друг от друга по своим преимущественным интересам, способностям, темпам мышления, складу характера, отношением к учителю. Казалось бы, в этих условиях их обучение должно быть строго индивидуальным. Однако, обучая целый классный коллектив, приходится основываться не на индивидуальных различиях, а на том общем, что роднит всех детей данной возрастной группы и на данной ступени обучения. Успешное обучение требует сочетания общей работы с индивидуальным подходом к каждому ученику.
В учебном процессе объективно возникает противоречие между коллективными формами обучения и индивидуальным характером усвоения знаний, умений и навыков. Это противоречие стимулирует меня к поиску эффективных путей дифференцированного подхода к каждому учащемуся, чтобы сделать обучение отвечающим особенностям личности ученика.
Наличие интереса к математике у учащихся является необходимым условием процесса обучения. Чем выше интерес, тем активнее идет обучение и тем лучше его результаты. Чем ниже интерес, тем формальнее обучение, хуже его результаты. Отсутствие интереса приводит к низкому качеству обучения, быстрому забыванию и даже полной потере приобретенных знаний , умений и навыков. Поэтому очень важно увеличить уровень интереса учеников к математике, следить за его изменением.
Технологии, построенные на объяснительно- иллюстративном способе обучения, дают низкий уровень навыков общения, невозможность получить развернутый ответ ученика с его собственной оценкой рассматриваемого вопроса, недостаточное включение слушающих ответ школьников в общее обсуждение. Информация учителя- это еще не знание ученика. Для того, чтобы перевести информацию в знание, учитель при традиционных методах обучения должен заставить ученика проделать достаточно огромную работу самостоятельно как в классе, так и дома, проконтролировать и оценить ее результативность.
Следовательно, развитие интеллекта школьников, творческого потенциала детей, обеспечение общей процедуры саморазвития личности должны не провозглашаться, а обеспечиваться технологически в учебном процессе, построенном на принципиально иных научно- методических основаниях. Необходим деятельностный способ обучения, который предполагает личностное включение школьника в процесс, когда компоненты деятельности им самим направляются и контролируются. Считаю наиболее приемлемым использование на уроках математики в 5- 6 классах технологии уровневой дифференциации и информационно-коммуникационных технологий, т.к. они дают гарантированный результат освоения базовых знаний всеми учащимися и одновременно возможности для каждого ученика реализовать свои склонности и способности.
«Различные задачи на взаимное расположение окружностей на плоскости»-второй урок по теме «Две окружности». Он опирается на знание геометрического материала по теме «Прямая и окружность», в частности понятии о касательной, и является основой для изучения темы «Построение треугольника».
Тип урока: Применение знаний и умений. Учебный материал урока имеет геометрическое содержание.
Этап урока «Занимательная математика» формировался из материала, изучаемого на занятиях математического кружка.
Информационные технологии применены для презентации исследовательского мини- проекта; для прохождения «Лабиринта», построенного на основе тестовых заданий; для выполнения индивидуальных дифференцированных заданий на построение. Проекты выполнялись учащимися на основе исследовательских задач вида: «Для каждого случая взаимного расположения двух окружностей определите, сколько можно провести различных прямых, касающихся обеих окружностей». В результате работы над проектом учащимися были сформированы папки с чертежами. Чертежи открываются при наличии программы «Живая геометрия» и соответствующих гиперссылок, которые при изменении электронного носителя необходимо сменить.
Тема: Различные задачи на взаимное расположение окружностей на плоскости.
Цель: Систематизация знаний о взаимном расположении окружностей и формирование умения решать задачи с опорой на знание зависимости радиусов окружностей и расстояния между их центрами
Задачи:
1. Обобщить и систематизировать знания учащихся о взаимном расположении окружностей на плоскости.
3. Формировать знания о зависимости радиусов окружностей и расстояния между их центрами.
4. Формировать познавательную мотивацию
5. Развивать пространственное представление, геометрическое мышление.
6. Развивать умения в работе с компьютерной программой «Живая геометрия»
7. Воспитывать интерес к изучению геометрического материала.
8. Воспитывать целеустремленность и дисциплинированность
Оборудование:
программа «Живая геометрия», компьютеры, чертежные инструменты, карточки с индивидуальными заданиями, мультимедийный проектор, экран, иллюстративное приложение для работы с компьютером.
Литература:
1.«Математика. 6 кл.» (авторы Г.В.Дорофеев, С.Б.Суворова, И. Ф. Шарыгин и др.; под ред. Г.В.Дорофеева и И.Ф. Шарыгина.-М.: Просвещение, 2004.)
2. Математика. 6 класс: поурочные планы по учебнику Г.В.Дорофеева, С.Б. Суворовой, И. Ф. Шарыгина и др. в двух частях/ авт.- сост. Т. Ю. Дюмина. – Волгоград: Учитель, 2006.
3. Манвелов С.Г. Конструирование современного урока математики. Кн. для учителя / С.Г.Манвелов. – М.: Просвещение, 2002.
Применяемые технологии: информационно-коммуникационные, уровневая дифференциация.
Методы: по источнику знаний - практический, наглядный;
по степени взаимодействия «учитель- ученик» - самостоятельная работа, беседа;
по характеру познавательной деятельности - исследовательский, частично- поисковый.
Формы учебный деятельности: индивидуальная, фронтальная.
I. Организационный момент.
II. Целеполагание. Составление программы деятельности на уроке.
III. Проверка домашней работы.
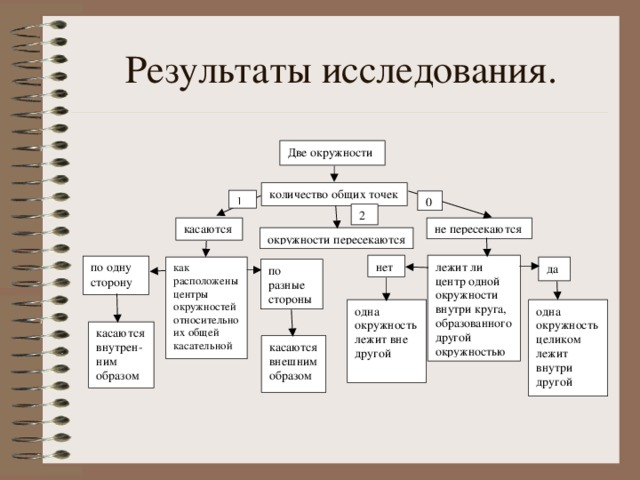
1. Формирование знаний о зависимости радиусов окружностей и расстояния между их центрами. Презентация проекта «Зависимость радиусов окружностей и расстояния между их центрами». (Приложение № 1 и компьютерная презентация в PowerPoint)
Содержание:
- Расстояние между центрами окружностей равно сумме их радиусов
- Расстояние между центрами окружностей меньше суммы их радиусов.
- Расстояние между центрами больше суммы двух радиусов.
- Расстояние между центрами равно разности двух радиусов.
- Расстояние между центрами окружностей равно нулю.
- Расстояние между центрами двух окружностей меньше разности радиусов.
2. Формирование умений и навыков по решению задач.
Задача № 509 а) Окружности касаются внешним образом. Радиус меньшей окружности равен 3 см. радиус большей- 5 см. Чему равно расстояние между центрами? Решение: 3+5=8(см)
Задача №509 б) Окружности касаются внутренним образом. Радиус меньшей окружности 3 см. Радиус большей окружности- 5 см. Чему равно расстояние между центрами окружностей? Решение: 5-3=2(см)
Задача №509 в) Окружности касаются внутренним образом. Расстояние между центрами окружностей 2,5 см. Чему равны радиусы окружностей?
ответ: (5,5 см и 3 см), (6.5 см и 4 см ) и т.д.
IV. Перенос приобретенных знаний в новые измененные условия с целью формирования умений решать задачи.
1.Задача №513 ОС=2 см,ОР=5 см, АР=? ВР=?
2. Представление проекта «Построение общих касательных к двум окружностям» (Приложение № 2 и компьютерная презентация «Построение общих касательных к двум окружностям»).
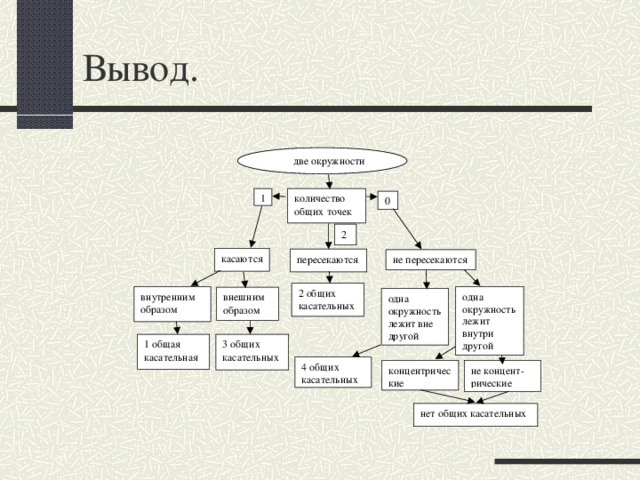
Содержание:
-4 общих касательных имеют не пересекающиеся окружности, когда расстояние между их центрами больше суммы радиусов.
-3 общих касательных имеют касающиеся окружности.
-2 общих касательных имеют пересекающиеся окружности.
-Одну общую касательную имеют окружности с внутренним касанием.
-Не имеют касательных концентрические окружности и окружности, расстояние между центрами которых меньше разности их радиусов.
V. Самостоятельная работа учащихся под руководством учителя.
1. Отработка практических умений по теме «Взаимное расположение окружностей на плоскости» на основе программы «Живая геометрия».
Учащимся предлагается выбрать карточки с индивидуальными заданиями:
-Постройте две окружности, расстояние между центрами которых равно нулю. Проведите общую касательную к этим двум окружностям.
-Постройте окружности, расстояние между центрами которых меньше разности их радиусов. Постройте общую касательную к этим двум окружностям.
-Постройте окружности, расстояние между центрами которых равно разности радиусов этих окружностей. Проведите общую касательную к этим окружностям.
- Постройте две концентрические окружности. Проведите третью окружность, чтобы она пересекала первые две окружности.
-Начертите две окружности разных радиусов, чтобы они касались. Отметьте отрезком расстояние между их центрами.
-Начертите две окружности разных радиусов, чтобы они пересекались. Отметьте отрезком расстояние между их центрами.
-Начертите две окружности разных радиусов, чтобы они не пересекались. Отметьте отрезком расстояние между их центрами.
-Постройте окружности, расстояние между центрами которых больше суммы их радиусов. проведите общие касательные к этим двум окружностям.
-Постройте окружности, расстояние между центрами которых меньше суммы их радиусов. Проведите общие касательные к этим двум окружностям.
- Постройте две окружности так, чтобы нельзя было провести общих касательных.
-Постройте две концентрические окружности. Проведите диаметры этих окружностей.
Комментарий к выполнению: Карточки имеют разный цвет в зависимости от уровня сложности. Учащиеся работают с программой «Живая геометрия» в парах: выполняют взаимопроверку и взаимооценивание.
2. Тестирование по теме «Взаимное расположение окружностей на плоскости».
Задание выполняется на основе дидактической игры «Лабиринт»
Содержание: Две окружности на плоскости либо пересекаются, либо не пересекаются (да - нет).
Если одна окружность проходит через центр другой окружности, то такие окружности пересекаются (да- нет)
Концентрические окружности - это окружности с общим центром (да- нет).
Две окружности, радиусы которых различны, могут касаться внутренним и внешним образом (да- нет).
Две окружности с равными радиусами могут касаться внутренним и внешним образом (да- нет)
Если окружности пересекаются, то расстояние между их центрами меньше суммы их радиусов (да- нет).
Если окружности не пересекаются, то расстояние между их центрами больше суммы их радиусов (да- нет).
У концентрических окружностей радиусы равны (да- нет).
Если окружности касаются внутренним образом, то расстояние между их центрами равно разности их радиусов (да- нет).
Если расстояние между центрами окружностей равно сумме их радиусов, то эти окружности касаются внешним образом (да- нет).
Можно провести только две окружности с общим центром, которые пересекали бы данную окружность (да- нет).
Можно провести только две окружности с общим центром, которые касались бы данной окружности (да- нет).
VI.Занимательная страничка. «Чем нас может удивить окружность?»
Учащиеся демонстрируют буклеты, над которыми работали во внеурочное время
VII. Обобщение и систематизация результатов выполненных заданий.
1.Проверка тестирования. Нахождение ключевого слова.
2. Взаимооценивание по итогам работы с программой «Живая геометрия».
VIII. Задание на дом.
Задача №515-повышенной сложности
Радиусы двух окружностей равны 3 см и 5 см, а расстояние между наиболее удаленными точками этих окружностей равно: а) 18 см, б)16 см, в) 13 см, г) 8 см
Задача №507- обязательного уровня.
-Начертите в тетради две равные окружности так, чтобы они пересекались; не пересекались. В каждом случае измерьте расстояние между центрами окружностей.
IX. Рефлексия.
-Что интересного и нового вы узнали об окружностях?