
Через математические знания лежит широкая дорога к огромным, почти необозримым областям труда и открытий.
Маркушевич А.И.
Экстремум функции двух переменных. Наибольшее и наименьшее значения

Цель занятия:
- закрепление знаний полученных на лекциях и применение их на практике;
- научить исследовать функцию нескольких переменных на максимум и минимум с использованием производных высших порядков;
- вывести алгоритм нахождения наименьшего и наибольшего значений функции; решать задачи на отыскание наибольших и наименьших значений функции;
- развитие пространственного мышления, умение планировать, мыслить логически и по аналогии.

(x ²)′=
0
(2x ³)′=
0
(x
10
) ′=
7
6x ²
(128 )′=
(10) ′=
1
(
x ³
) ′=
9
10x
3
2x
x ²
10x + 3
(7x )′=
(5x ² + 3x - 9 )′=
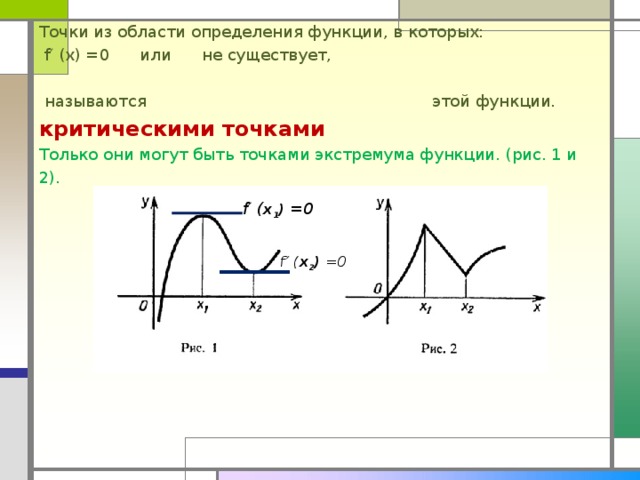
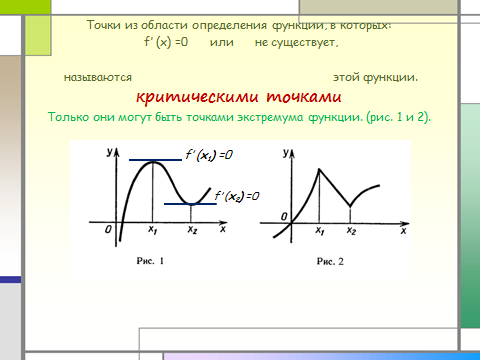
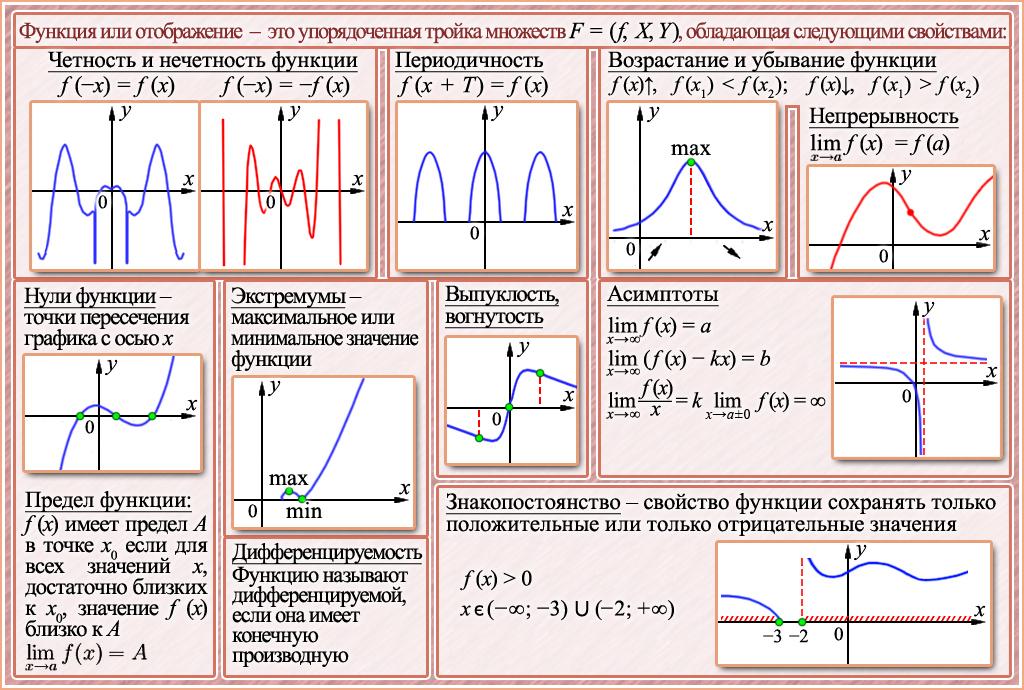
Точки из области определения функции, в которых:
f′ (x) =0 или не существует,
называются этой функции.
критическими точками
Только они могут быть точками экстремума функции. (рис. 1 и 2).
f′ ( x 1 ) =0
f′ ( x 2 ) =0
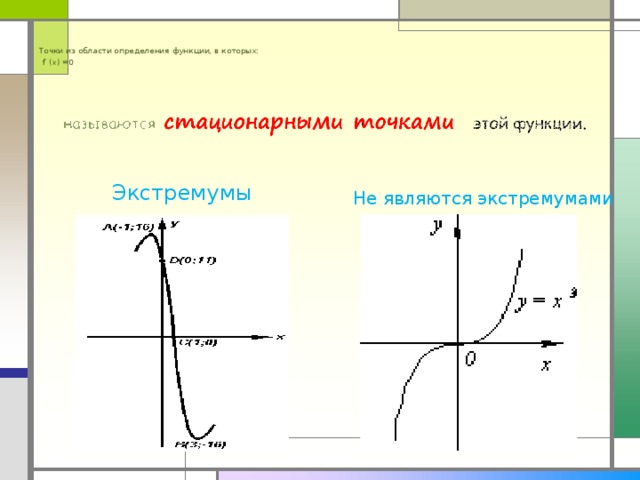
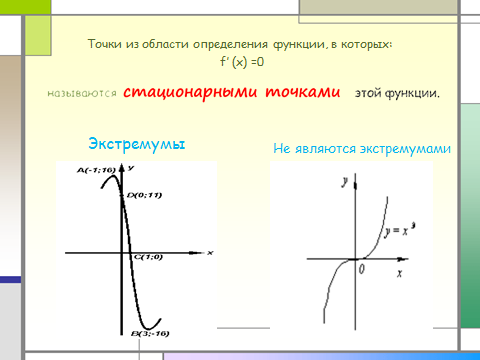
Точки из области определения функции, в которых: f′ (x) =0
Экстремумы
Не являются экстремумами
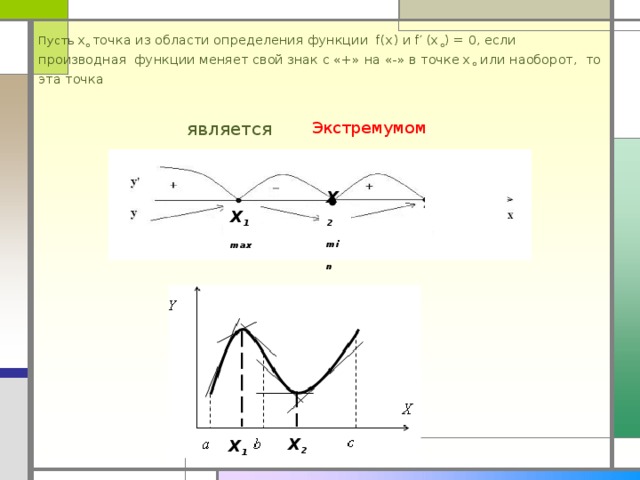
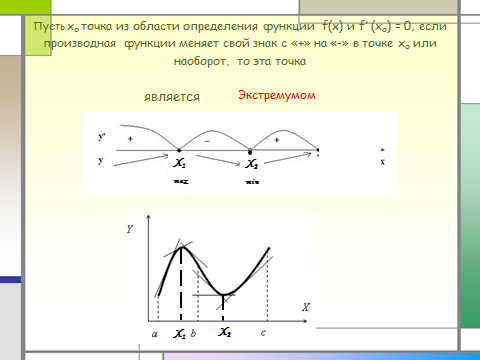
Пусть x о точка из области определения функции f(x) и f′ (x о ) = 0, если производная функции меняет свой знак с «+» на «-» в точке x о или наоборот, то эта точка
является
Экстремумом .
Х 1
Х 2
max
min
Х 2
Х 1
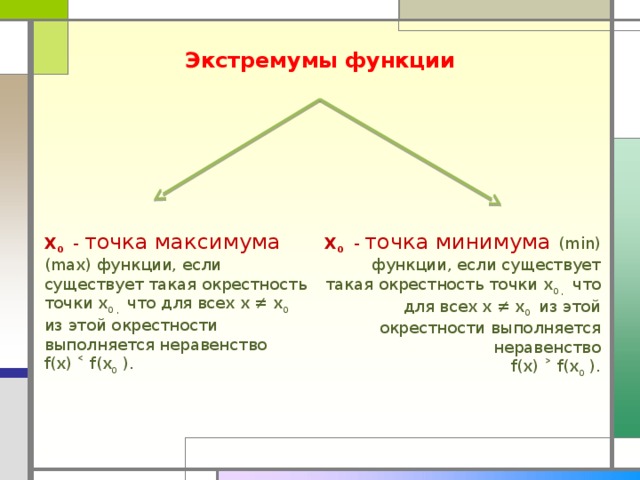
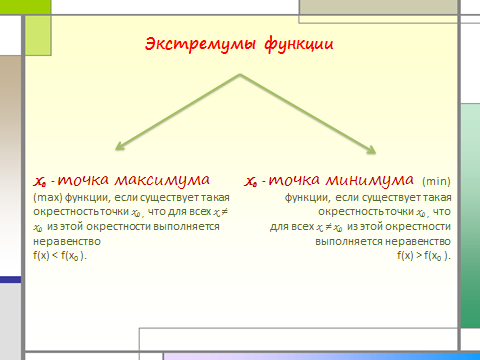
Экстремумы функции
Х 0 - точка максимума (max) функции, если существует такая окрестность точки х 0 , что для всех х ≠ х 0 из этой окрестности выполняется неравенство
f(x) ˂ f(x 0 ).
Х 0 - точка минимума (min)
функции, если существует такая окрестность точки х 0 , что
для всех х ≠ х 0 из этой окрестности выполняется неравенство
f(x) ˃ f(x 0 ).
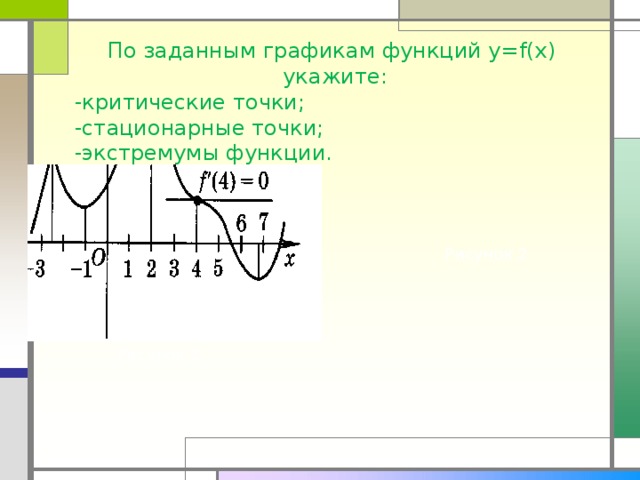
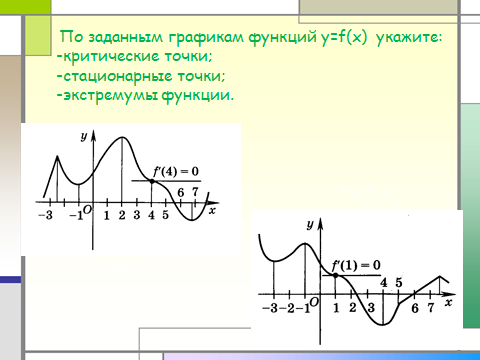
По заданным графикам функций y=f(x) укажите:
-критические точки;
-стационарные точки;
-экстремумы функции.
Рисунок 2
Рисунок 1
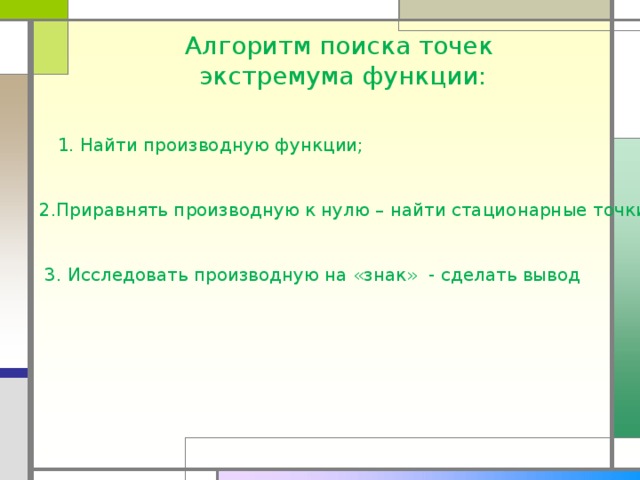
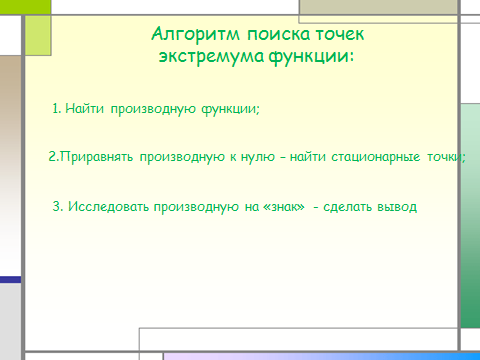
Алгоритм поиска точек экстремума функции:
1. Найти производную функции;
2.Приравнять производную к нулю – найти стационарные точки;
3. Исследовать производную на «знак» - сделать вывод .

Выполните задание
1.Найдите точку максимума функции
на (0; )
2.Наидите точку минимума функции
на (0; )
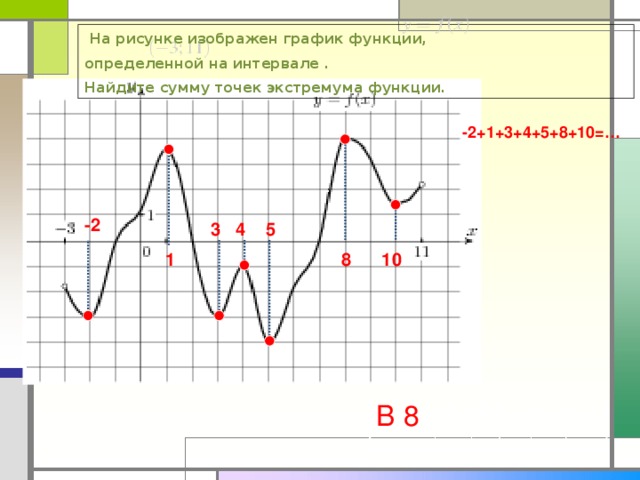
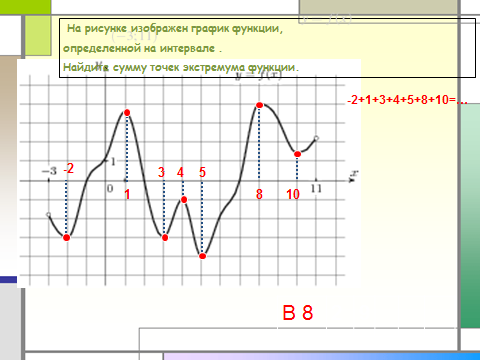
На рисунке изображен график функции,
определенной на интервале .
Найдите сумму точек экстремума функции.
-2+1+3+4+5+8+10=…
-2
5
4
3
.
10
8
1
В 8
2
9
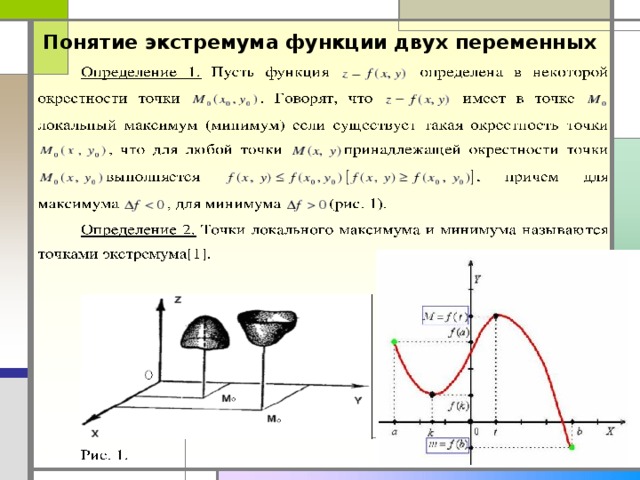
Понятие экстремума функции двух переменных





вторых производных и найдем знак дискриминанта
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
11

Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, в так называемых задачах на оптимизацию.
ПРИМЕР. Рекламный щит имеет форму прямоугольника S=9 м 2 . Изготовьте щит в виде прямоугольника с наименьшим периметром
![Решение: Пусть x(м) – длинна, 9/x(м) – ширина рекламного щита. P – Периметр P=2(x+9/x)м; P(x)=2x+18/x; P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m P(x)=2x+18/x P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m S=9m 2](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_19.jpg)
Решение:
Пусть x(м) – длинна,
9/x(м) – ширина рекламного щита.
P – Периметр
P=2(x+9/x)м; P(x)=2x+18/x; P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m P(x)=2x+18/x P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m S=9m 2

![Задание 1. Найти наибольшее и наименьшее значение функции у = х³ - 3х² - 45х + 1 на [-4; 6] без построения графика.](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_21.jpg)
Задание 1.
Найти наибольшее и наименьшее значение функции у = х³ - 3х² - 45х + 1 на [-4; 6]
без построения графика.

АЛГОРИТМ
- Найти точки экстремума функции, т. е. точки в которых производная равна нулю и меняет свой знак.
- Вычислить значение функции в этих точках и на концах отрезка, где определена функция.
- Выбрать из полученных значений оптимальное.
- Перевести задачу на язык математики, т. е. выразить искомую величину через функцию от некоторой переменной и найти область её определения.
![Задание 2. Найти наибольшее и наименьшее значение функции у = х³ - 5х² + 7х на [-1; 2] без построения графика. Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_23.jpg)
Задание 2.
Найти наибольшее и наименьшее значение функции у = х³ - 5х² + 7х на [-1; 2]
без построения графика.
Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3

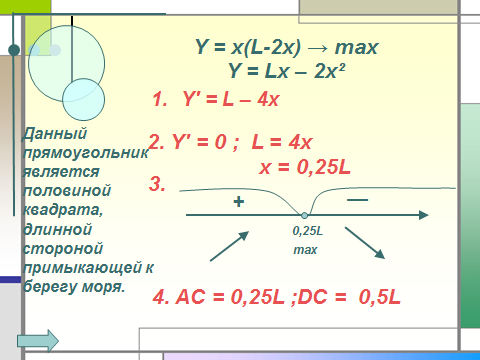
Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно огородить её одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремешки, связала их и огородила полученным ремнём большой участок земли, примыкавший к побережью.
Вопрос: какую наибольшую площадь земли могли купить финикийцы?

Переведём задачу на язык математики.
B
A
AC+CD+DB=L
x
x
D
C
L - 2x
S = x(L-2x)
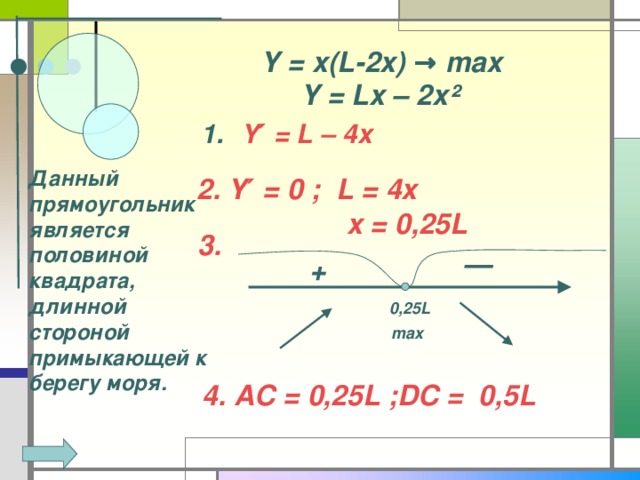
Y = x(L-2x) → max
Y = Lx – 2x ²
Данный прямоугольник является половиной квадрата, длинной стороной примыкающей к берегу моря.
2. Y′ = 0 ; L = 4x
x = 0,25L
3.
—
+
0,25L
max
4. AC = 0,25L ;DC = 0,5L

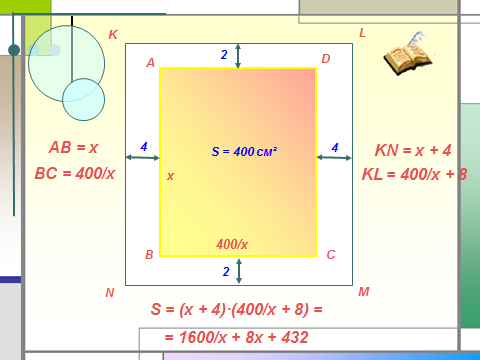
Печатный текст (вместе с промежутками между строками) одной страницы книги должен занимать 400 см ². Верхние и нижние поля страницы должны иметь ширину 2 см. Боковые – 4 см.
Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?
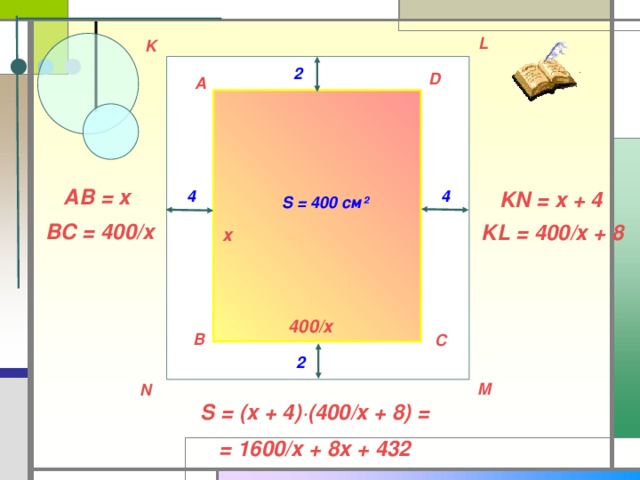
L
K
2
D
A
AB = x
4
KN = x + 4
4
S = 400 см ²
BC = 400/x
KL = 400/x + 8
х
400/х
B
C
2
M
N
S = (x + 4) ·(400/x + 8) =
= 1600/x + 8x + 432
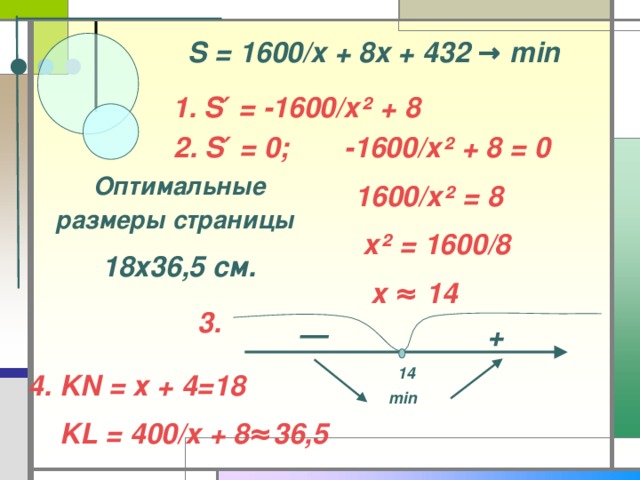
S = 1600/x + 8x + 432 → min
1. S ′ = -1600/x² + 8
2. S′ = 0; -1600/x² + 8 = 0
1600/x² = 8
x² = 1600/8
x ≈ 14
Оптимальные размеры страницы
18х36,5 см.
3.
—
+
14
4. KN = х + 4=18
KL = 400/x + 8 ≈36,5
min










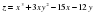 .
.
 ;
;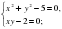
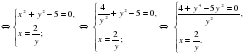
 . Дробь равна нулю, когда ее числитель равен нулю, т.е.
. Дробь равна нулю, когда ее числитель равен нулю, т.е. 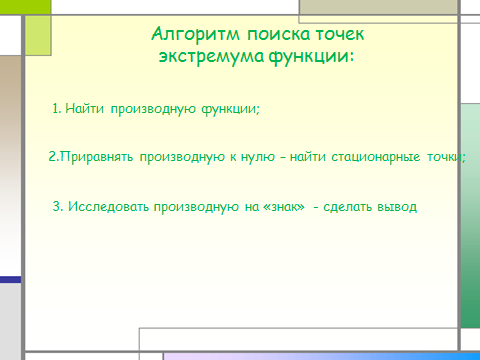


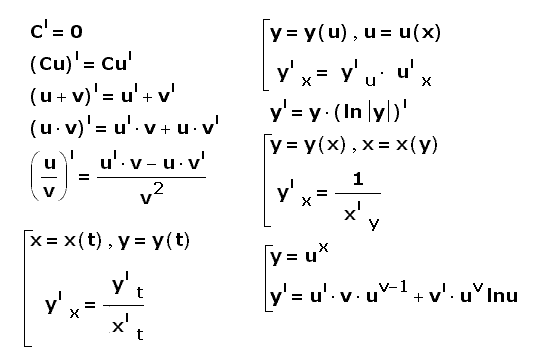




















![Решение: Пусть x(м) – длинна, 9/x(м) – ширина рекламного щита. P – Периметр P=2(x+9/x)м; P(x)=2x+18/x; P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m P(x)=2x+18/x P(x)=2-18/ X 2 на [1;9] 2-18/ X 2 =0 x не равно 0 2X 2 -18=0 X 2 =9 X=3 P(1)=2+18=20 P(9)=18+2=20 P(3)=6+6=12 Min P(3)=12m S=9m 2](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_19.jpg)

![Задание 1. Найти наибольшее и наименьшее значение функции у = х³ - 3х² - 45х + 1 на [-4; 6] без построения графика.](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_21.jpg)

![Задание 2. Найти наибольшее и наименьшее значение функции у = х³ - 5х² + 7х на [-1; 2] без построения графика. Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3](https://fsd.kopilkaurokov.ru/uploads/user_file_547cc52775306/img_user_file_547cc52775306_2_23.jpg)























