| Составители: Истомина Т.Г., Маличенко Н.Ф., Ващенко Л.В. МБОУ «Гимназия № 1» |
| Предмет | Математика | Класс | 9 |
| Авторы УМК | А.Г.Мордкович |
| Тема учебного занятия | Геометрическая прогрессия |
| Тип учебного занятия | Урок изучения нового материала |
| Цели учебного занятия | - организовать деятельность по выводу формул ГП и их использованию;
- создать условия для формирования навыков работы в команде, умения высказывать и аргументировано отстаивать своё мнение;
- сформировать умение у учащихся брать на себя ответственность при руководстве мини-группой;
- корректировать грамотное использование математических терминов в речи учащихся; |
| Планируемые образовательные результаты |
| Предметные | Мета предметные | Личностные |
| - умеет применять индексные обозначения; - распознает АП и ГП при разных способах задания, устанавливает закономерность, если даны несколько ее первых членов; - вычисляет члены последовательностей, заданных формулой n-го члена или рекуррентной формулой; - умеет анализировать текстовые задачи; - грамотно применяет математическую терминологию и символику;
| Познавательные УУД П1 – умеет применять формулы АП, ГП; П2 – составляет схемы определения понятия, подведение под понятие; П3 - постановка и решение проблемы при составлении задачи; П4 – проводит сравнение, П5 - проводит обобщение, П6 – проводит анализ; П7 – проводит классификации; П8 – выбирает задачи в соответствии с целью; П9 – проводит дедуктивные рассуждения (от правил к примеру); П10 – проводит смысловую работу с текстом; П11 - ставит цели, отличать гипотезу от факта;
Регулятивные УУД Р1 – формулирует цель учебной деятельности; Р2 - осуществляет выбор плана действий для достижения цели; Р3 - осуществляет самоконтроль; Р4 - осуществляет самопроверку с использованием образцов, приёмов; Р5 - оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; Р6 – осуществляет контроль, оценку и коррекцию; Р7 - умение контролировать процесс и результат учебной деятельности Коммуникативные УУД К1 - работает в группе, оказываете взаимопомощь, рецензирует ответы товарищей; К2 - организует взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; К3 - оказывает помощь, работающим на предыдущих уровнях; К4 – умеет делать выбор; К5 - умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;
| Л1 – самоопределение; Л2 – рефлексия собственной деятельности; Л3 – понимание значение умений для решения задач на ГП; Л4 - способность к эмоциональному восприятию математических объектов; Л5 - креативность мышления, инициатива, находчивость, активность; Л6 - готовность и способность обучающихся к саморазвитию и личностному самоопределению;
|
| Технологии обучения | Деятельностного типа |
| Методы обучения
| Частично-поисковый, объяснительно-иллюстративный, проблемно-поисковый (организация коллективной работы в парах). |
| Средства обучения | Учебник, тетрадь, дневник, доска, мел, проектор. |
| Необходимое аппаратное и программное обеспечение | Презентация, карточки |
| Дидактические разработки
| карточки – задания для самостоятельной работы, раздаточный материал на каждого, задания в презентации, карточки с изображением смайликов для рефлексии. |
|
Организационная структура урока |
| Этапы урока | Деятельность учителя | Деятельность учащихся | Развиваемые УУД |
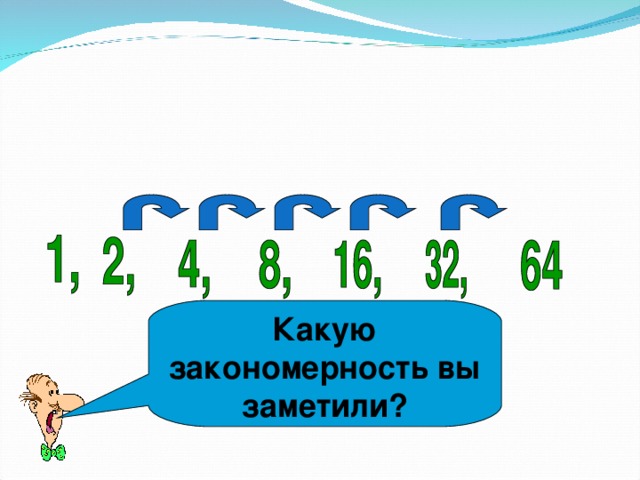
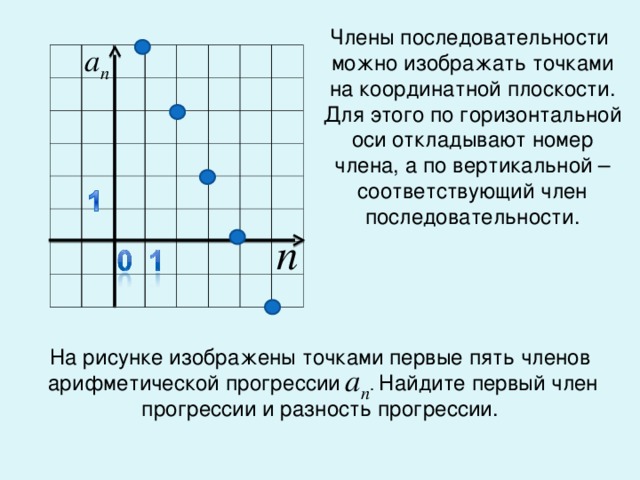
| I.Организационно-мотивационный этап. Целеполагание. (2 мин) | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Слайд 1. Русская народная сказка «Лисичка-сестричка и волк». Наловил дед рыбы полный воз. Рыба - крупные лещи. Едет домой и видит, лисичка свернулась калачиком лежит на дороге. Дед решил, что она мертвая. Вот славная находка! Будет моей старухе воротник на шубу. А лиса улучила время и стала выбрасывать полегоньку из воза все по рыбке да по рыбке. В первую минуту - 1 леща, во вторую–2-х, в третью-4-х , а в четвертую-8-х. Сколько лещей она выкидывала в пятую, шестую, седьмую минуты. Составьте последовательности. Слайд 2. Какую закономерность вы заметили?
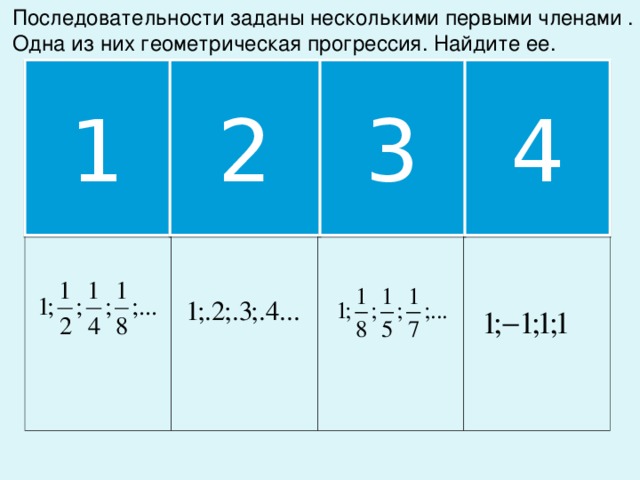
Слайд 3. Среди последовательностей, выберите те, которые подчиняются этому закону: 1,2,3,4,5… 5,5,5,5,5… 2,4,8,16,32… -1,3,-9,27… 3,5,7, 9…. Какой вывод о данных последовательностях мы можем сделать? Слайд 4. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. | Приветствуют учителя, включаются в учебную деятельность.
1,2,4,8,16.32.64. Каждый член числовой последовательности отличается от предыдущего умножением на одно и тоже число.
Каждый член числовой последовательности отличается от предыдущего умножением на одно и тоже число.
| Л3, П9, П10
П4, П6, Л4, Л5
П4, П6, Л4,Л5, Р4 |
| II. Актуализация опорных знаний. Устная работа (8 мин)
| Слайд 5-6. Какие еще последовательности мы изучали с вами, в которых так же есть некая закономерность?
Есть необходимость вспомнить определение и свойства АП? 1) Последовательность, каждый член которой больше предыдущей называется арифметической прогрессией. 2) Числовая последовательность, каждый член которой, начиная со второго равен сумме предыдущего и одного и того же числа, называется арифметической прогрессией 3) d- разность арифметической прогрессии 4) d = а3 - а1 5) d = а2 – а1 6) аn = а1 + d (n-1) - формула n-ого члена арифметической прогрессии 7) а7= а1+6d 8) 23 =6 9) 2 4= 16 10) 33 = 9 11) 33 = 2 |
Да, арифметическую
Отвечают да, нет. нет
да
да нет да да да нет да нет нет | П1, П2, П6, Л4, Л5, К4, К5
|
| III. Мотивация учебной деятельности (9 мин)
Исторический материал | Итак, что мы знаем про арифметическую прогрессию?
Как вы думаете, для ГП можно найти что то общее с АП? Что целесообразно для этого сделать? Слайд 7. Знать определение ГП; Найти связь между членами ГП; Узнать формулу n-го члена ГП и формулу суммы n-первых членов ГП;
А можем ли мы, зная формулы АП вывести формулы ГП?
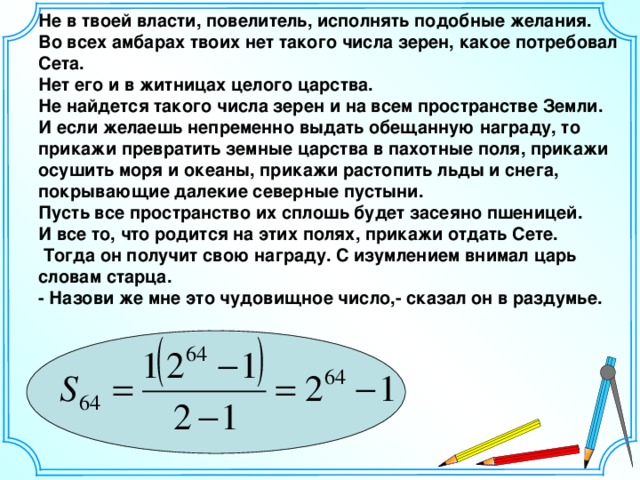
Вы на верном пути. Предлагаю вам ознакомиться с некоторыми историческими фактами. Слайд 8-9. Слово (прогрессия) латинского происхождения, означает движение вперед и встречается впервые у римлян в V- V1 вв.. Некоторые формулы прогрессии были известны китайским и индийским математикам еще до н.э. Шотландскому математику Джону Неперу принадлежит идея о том, что от свойств арифметической прогрессии можно перейти к аналогичным свойствам геометрической прогрессии с положительными членами, если сложение и вычитание соответственно заменить умножением и делением, а умножение и деление – возведение в степень и извлечение корня. После такой замены остаются в силе не только формулировки свойств, но и доказательства. Проверим принципы Непера на практике. | - определение; - формулу n-го члена; - разность АП; - формулу суммы n-первых членов АП;
Учащиеся формулируют цели урока.
Учащиеся предлагают варианты формул, глядя на предложенные ранее последовательности.
Слушают, рассуждают | П2, П5, П11, Р1, Л5, Л6, К4, К5
Л3, Л4
|
| IV. Восприятие и осознание учащимся нового материала | Каждому раздаются опорные карты: примените идею Непера и запишите формулы нахождения знаменателя и n-ого члена геометрической прогрессии an =a1 +(n -1) d d = а n– аn-1 Слайд 10. Проверьте ваши формулы на одной из последовательностей, предложенных ранее.
| bn = b 1 qn-1 q = bn : bn-1
Дети выбирают любую последовательность и убеждаются в правильности решения. | П1, П8, П9, П10, Л3, Л5, Л6, Р2, К5 |
| Закрепеление во внешней речи. | Попробуйте сформулировать что такое q и как звучит формула для нахождения n-го члена ГП.
Слайд 11 На экране появляются правила. | Рассуждают, пытаются сформулировать правила. | П1, П2, П5, П6, П10, Р3, Р4, К5, Л2, Л3, Л4, Л6 |
| V. Закрепление
| Как мы можем с вами закрепить полученные знания и научиться применять формулы ГП? С помощью каких типов заданий, мы можем научиться применять формулы ГП? Вы молодцы. Сегодня я подобрала для вас задания этих типов. Сейчас я вам раздам карточки. Вы в паре выполняете это задание. После этого мы проверим ваши решения.
Слайд 12. Даны геометрические прогрессии. Найдите q=3, b4. А)1; 3; 9;… Б) 3; 3/2, ¾… В) 8; 8; 8; Г) 2, -2, 2,…. | Учащиеся предлагают варианты (карточки, учебник, придумать самим)
q=3, b4 =27 q = 1/2, b4=3/8 q = 1 b 4= 8 q = -1 b4 = -2 | П1, П6, П8, Л3, Л4, Л5, Р2, Р3, Р4, Р5, Р6, Р7, К1, К2, К3 (для слайдов 10-15) |
|
| Слайд 13. Составить формулу n-ого члена геометрической прогрессии. 2,4,8,16….. 5, 10, 20, 40, …. 1, ½,1/4,1/8 |
bn = 2* 2n-1 bn=5* 2n-1 bn-= 1*(1/2)n-1 |
|
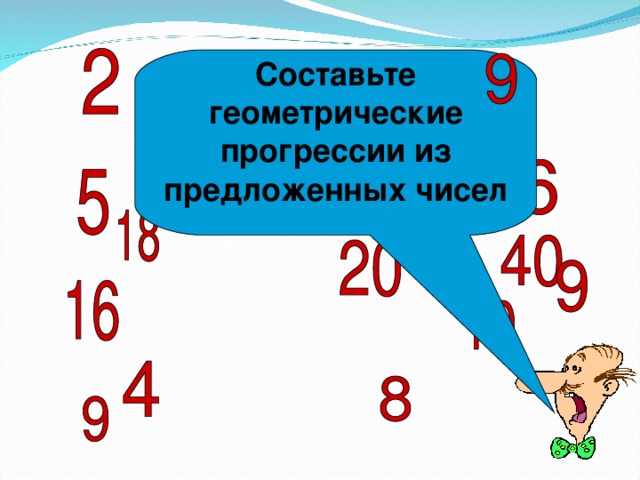
|
| Слайд 14. Составьте геометрические прогрессии: 1;8;9;16;27;5;9;2;20;9;2;4;9;10;3;40 | 1;3;9;27.. 5;10;20;40.. 16;8;4;2… 9;9;9;9… |
|
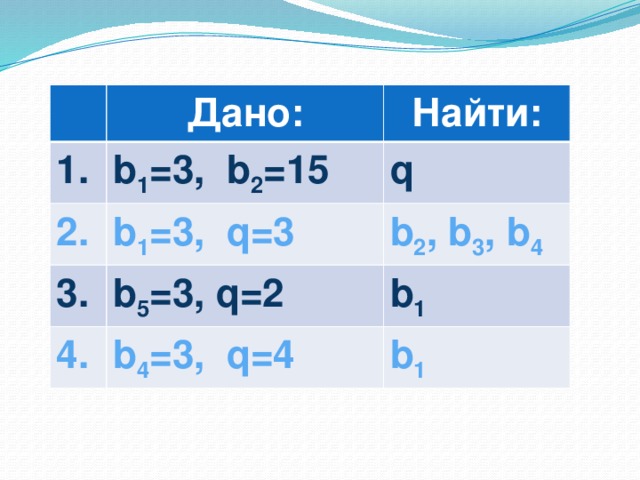
|
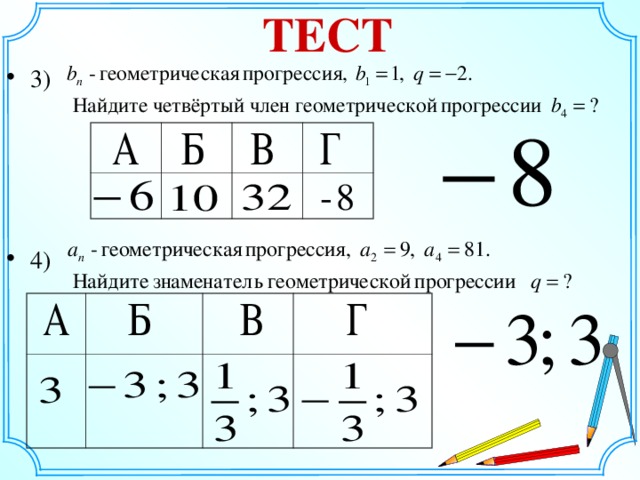
| Слайд 15. Даны геометрические прогрессии. Известно: 1) b1= 1 /4 q=1\2, найти b3-? 2) b1=2 q=3, найти b4-? 3) b1=3 q=-2, найти b3-? 4) b1=2 q=-1\2, найти b4-? |
b3=1/16 b4=54 b3=12 |
|
|
| Слайд 16. Дана геометрическая прогрессия: b1; b2; b3 …………. Известно: что b7=7/32, b1=14, найти знаменатель? |
q=1/2 |
|
|
| Слайд 17-19. Составьте геометрическую прогрессию: Ежедневно каждый болеющий гриппом может заразить четырех окружающих. Какой вывод мы можем сделать? Дима на перемене съел булочку, не помыв руки. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 минут происходит деление бактерий (они удваиваются). Какой вывод мы можем сделать? Каждый курильщик выкуривает в среднем 8 сигарет в сутки. После выкуривания одной сигареты в легких оседает 0,0002 грамма никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается в два раза. Какой вывод мы можем сделать? |
1;4;16;64;… Нельзя больным ходить в школу. 30;60;120;240;… Нужно мыть руки перед едой.
0,0002;0,0004;0,0008;… Нужно вести здоровый образ жизни. |
|
| Рефлексия | Ребята, получилось ли у нас достичь целей, которые мы поставили с вами на уроке? Знать определение ГП; Найти связь между членами ГП; Узнать формулу n-го члена ГП и формулу суммы n-первых членов ГП;
|
Да Да Да | П5, П6, К5 |
| Домашнее задание | Слайд. |
|
|
| Рефлексия | Приведите примеры ЧП в жизни человека. | Дни недели, возраст человека, название месяцев, нумерация домов, и т.д. | П1, П4, П5, П10, Л4, Л5, Р4, К4, К5 |
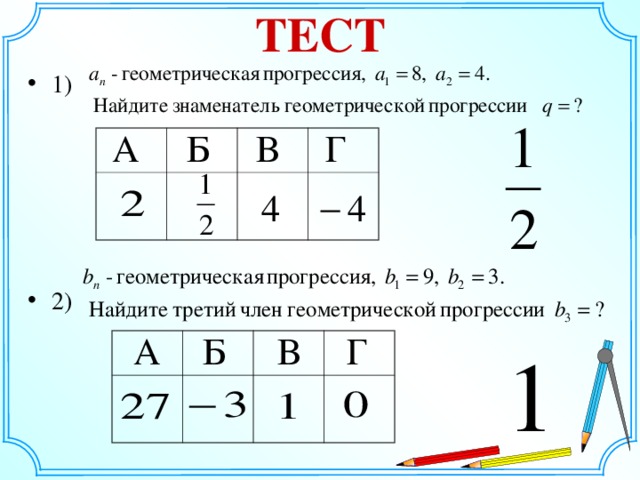
| 1) Является ли число ¼ членом геометрической прогрессией 8;4;2….. 2)Впишите пропущенные члены геометрической прогрессии А)___;1;4;___64;… Б) 4;___;36;108.. | Да
А) ¼;16 Б) 12 |
|
| Возьмите карточку и поставьте себе оценку за урок, затем возьмите карточку соседа по парте и поставьте ему оценку. | 5, 5, 5, 5 и т.д. | Р5, Л1, Л2, Р6, К4, К5 |
Шотландскому математику Джону Неперу принадлежит идея о том, что от свойств арифметической прогрессии можно перейти к аналогичным свойствам геометрической прогрессии с положительными членами, если сложение и вычитание соответственно заменить умножением и делением, а умножение и деление – возведение в степень и извлечение корня.
Даны геометрические прогрессии. Найдите q=3, b4. А)1; 3; 9;… Б) 3; 3/2, ¾… В) 8; 8; 8; Г) 2, -2, 2,…. | Даны геометрические прогрессии. Найдите q=3, b4. А)1; 3; 9;… Б) 3; 3/2, ¾… В) 8; 8; 8; Г) 2, -2, 2,…. |
Составить формулу n-ого члена геометрической прогрессии. 2,4,8,16….. 5, 10, 20, 40, …. 1, ½,1/4, 1/8 | Составить формулу n-ого члена геометрической прогрессии. 2,4,8,16….. 5, 10, 20, 40, …. 1, ½,1/4, 1/8 |
Составьте геометрические прогрессии: 1;8;9;16;27;5;9;2;20;9;2;4;9;10;3;40 | Составьте геометрические прогрессии: 1;8;9;16;27;5;9;2;20;9;2;4;9;10;3;40 |
Даны геометрические прогрессии. Известно: 1) b1= 1 /4 q=1\2, найти b3-? 2) b1=2 q=3, найти b4-? 3) b1=3 q=-2, найти b3-? 4) b1=2 q=-1\2, найти b4-? | Даны геометрические прогрессии. Известно: 1) b1= 1 /4 q=1\2, найти b3-? 2) b1=2 q=3, найти b4-? 3) b1=3 q=-2, найти b3-? 4) b1=2 q=-1\2, найти b4-? |
Дана геометрическая прогрессия: b1; b2; b3 …………. Известно: что b7=7/32, b1=14, найти знаменатель? | V. Дана геометрическая прогрессия: b1; b2; b3 …………. Известно: что b7=7/32, b1=14, найти знаменатель? |
| VI. Составьте геометрическую прогрессию: Ежедневно каждый болеющий гриппом может заразить четырех окружающих. Какой вывод мы можем сделать? Дима на перемене съел булочку, не помыв руки. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 минут происходит деление бактерий (они удваиваются). Какой вывод мы можем сделать? Каждый курильщик выкуривает в среднем 8 сигарет в сутки. После выкуривания одной сигареты в легких оседает 0,0002 грамма никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается в два раза. Какой вывод мы можем сделать? | VI. Составьте геометрическую прогрессию: Ежедневно каждый болеющий гриппом может заразить четырех окружающих. Какой вывод мы можем сделать? Дима на перемене съел булочку, не помыв руки. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 минут происходит деление бактерий (они удваиваются). Какой вывод мы можем сделать? Каждый курильщик выкуривает в среднем 8 сигарет в сутки. После выкуривания одной сигареты в легких оседает 0,0002 грамма никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается в два раза. Какой вывод мы можем сделать? |







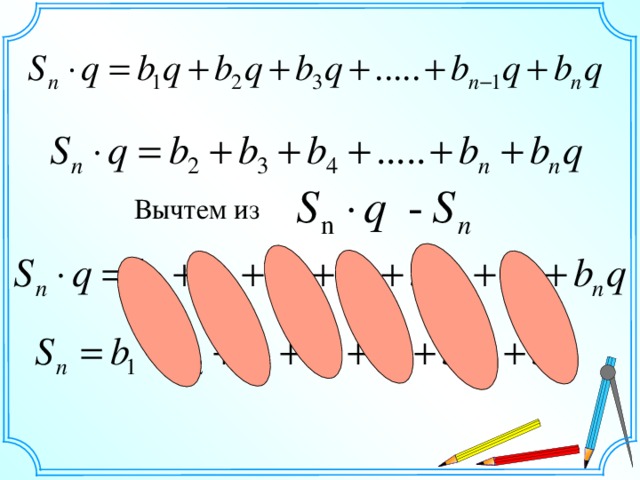
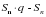 Вычтем из
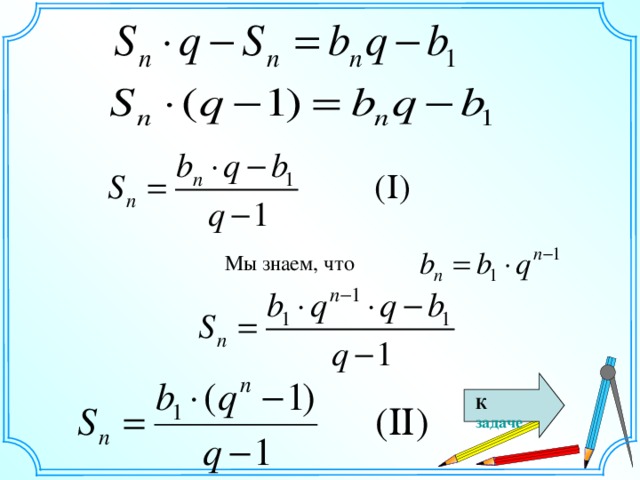
Вычтем из 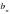 члена геометрической прогрессии и выведите вторую формулу суммы членов конечной геометрической прогрессии.
члена геометрической прогрессии и выведите вторую формулу суммы членов конечной геометрической прогрессии. 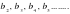
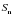 - в правой части есть противоположные слагаемые, которые взаимно уничтожаются;
- в правой части есть противоположные слагаемые, которые взаимно уничтожаются;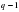 .
.