| Этапы урока, время | Учитель
| Ученики | Доска и оборудование | Формируемые УУД |
| Актуализация знаний 1 минута
| Сегодня у нас новая тема. Какая? Вы сейчас ее определите сами. Выполните следующее задание. Постройте окружность. Разделитесь на два варианта.
|
|
|
|
| Создание проблемной ситуации 3 минуты
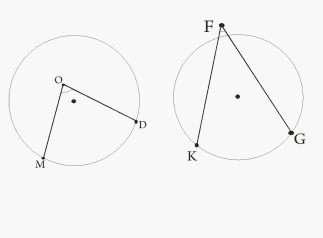
| I вариант: постройте угол МОР с вершиной в центре окружности (стороны угла пересекают окружность). II вариант: постройте угол АВD, вершина которого принадлежит окружности, а стороны пересекают эту окружность. Проверим возможные построения по готовым чертежам: 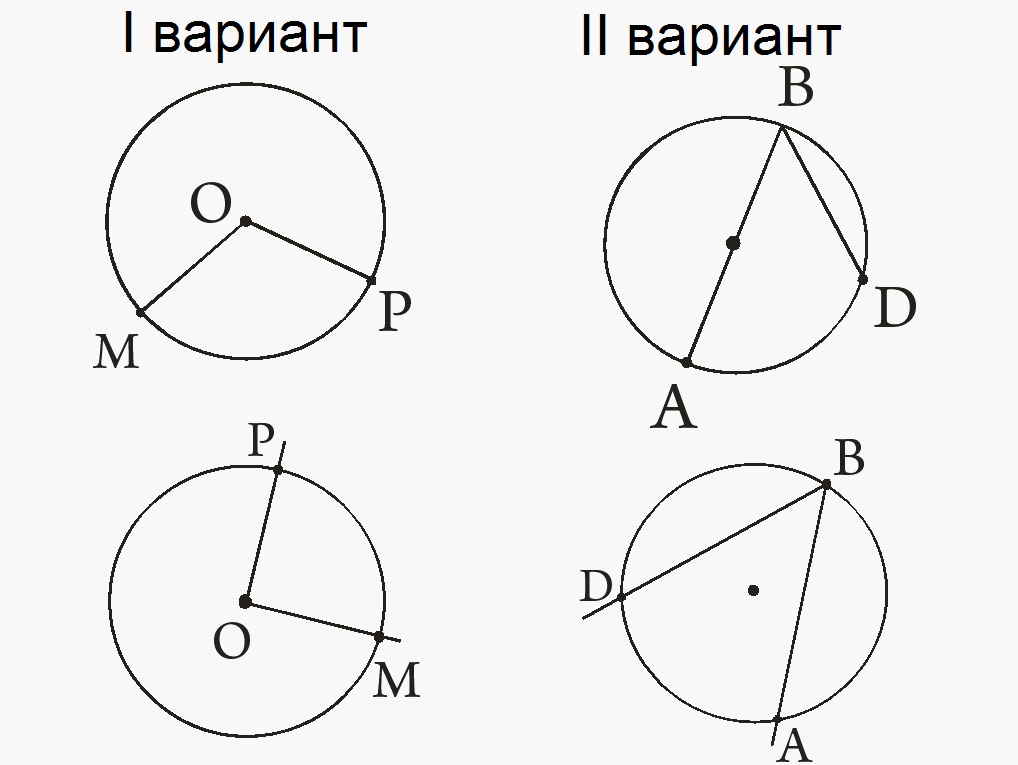
|
| На доску с помощью магнитов прикрепляются готовые чертежи | Познавательные |
| Формулирование проблемы 2 минуты | Что общего у построенных нами углов? А есть ли у этих углов различия? Значит, что мы сейчас будем исследовать? Что скажете о вершинах углов в 1 и 2 вариантах?
| Они связаны с окружностью. Да. Чем эти углы различаются. У 1 варианта вершина совпадает с центром окружности, у 2 варианта вершина лежит на окружности.
|
| Познавательные |
| Открытие нового знания 5минут
Формулирование нового знания 2 мин. | Такие углы имеют специальные названия. Угол МОР называют центральным углом, угол ABD называют вписанным углом. Попробуйте дать определение центрального угла. Продолжите предложение: центральным углом называется угол... ( далее ученики заканчивают фразу). Попытайтесь дать определение вписанного угла. Продолжите предложение: вписанным углом называется угол……… (далее ученики заканчивают предложение). Угол МОР опирается на какую дугу? Угол АВD опирается на какую дугу?
Так какую тему мы сегодня с вами изучаем?
Проверьте правильность сформулированных определений по учебнику на стр. 170.
|
вершина которого совпадает с центром окружности
вершина которого лежит на окружности, а стороны пересекают эту окружность
дугу МР дугу АD
Центральные и вписанные углы.
| Учебник. Геометрия. 7-9 классы. Под ред. Л.С. Атанасяна | Познавательные |
| Первичное применение нового знания 3 минуты | Закрепим понятие вписанного угла по готовым чертежам : назовите только вписанные углы и дуги, на которые они опираются.
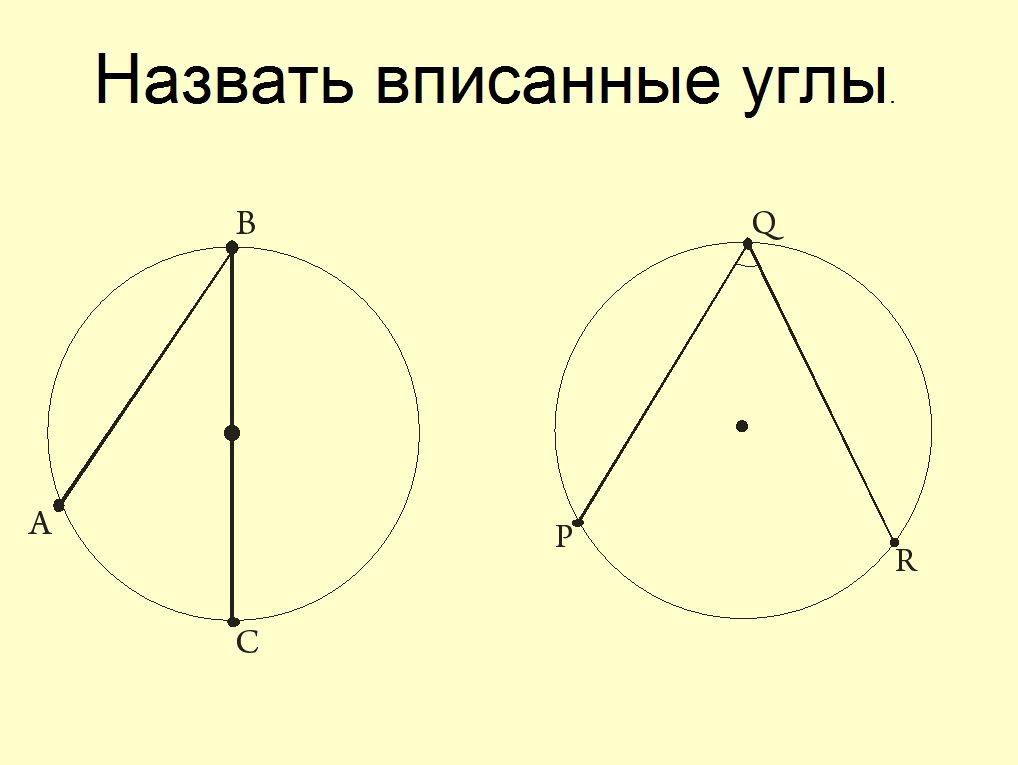
 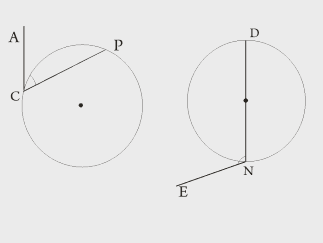
Будет ли угол МОД центральным? |
Угол ABC опирается на дугу AC Угол PQR опирается на дугу PR
Нет, так как его вершина не лежит в центре окружности. |
На доску с помощью магнитов прикрепляются готовые чертежи |
Познавательные |
| Самостоятельная работа 9 минут |
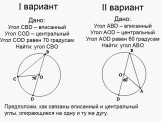
У каждого из вас на парте лежит карточка с задачей. Она дана с подсказками для тех, кто будет испытывать трудности при решении. Параллельно два человека из разных вариантов решат эту задачу с карточки на оборотной стороне доски (у доски работают два, более способных, ученика; учитель контролирует их решение). Подсказки для I варианта(II варианта): 1.Рассмотрите треугольник COB (AOB). Является ли он равнобедренным? Какие его стороны равны и почему? Какие углы равны? 2.Будет ли угол COD(AOD)внешним углом треугольника COB (AOB)?
3. Каким свойством обладает внешний угол треугольника? 4. Найдите градусную меру угла OBC(ABO)
Послушаем решение каждого ученика, решавшего задачу на доске. Вы, ребята, проверьте решение задачи и ответ с записями на доске. (самопроверка) |
I ВАРИАНТ: 1. Рассмотрим треугольник COB. Он является равнобедренным, OC= OB ( как радиусы). У равнобедренного треугольника углы при основании равны, то угол ОCВ равен углу СВО. 2. Угол COD- внешний угол этого треугольника. 3. По свойству внешнего угла: угол COD равен сумме двух углов треугольника, не смежных с ним, т.е. угол COD равен сумме углов ОCВ и СBО. угол COD равен сумме углов ОCВ и СBО. 4. Угол CBO равен половине угла СOD, т.е. 35 градусов(70 делим на 2). Ответ: 35 градусов.
II ВАРИАНТ: 1. Рассмотрим треугольник АOB. Он является равнобедренным, OА= OB ( как радиусы). У равнобедренного треугольника углы при основании равны, то угол АВО равен углу ОАВ. 2. Угол АOD- внешний угол этого треугольника. 3. По свойству внешнего угла: угол АOD равен сумме двух углов треугольника, не смежных с ним, т.е. угол АOD равен сумме углов ОАВ и АBО. угол АOD равен сумме углов ОАВ и АBО. 4. Угол АBO равен половине угла АOD, т.е. 30 градусам(60 делим на 2). Ответ: 30 градусов. (Учащиеся проверяют решения, вносят при необходимости исправления в свои записи). |
Карточки с задачей на два варианта |
Познавательные
Регулятивные |
| Открытие нового знания 10 минут
| На стр. 170 учебника найдите ответ на вопрос: Чему равна градусная мера дуги СД по рисунку задачи 1 варианта? Чему равна градусная мера дуги АД по рисунку задачи 2 варианта?
Вспомните условия и ответы задач в 1 и 2 вариантах. Как связаны вписанные углы СВД и АВД с дугами СД и АД, на которые они опираются?
Есть гипотезы?
Выше мы с вами сделали вывод, что градусная мера дуги равна градусной мере центрального угла ,опирающегося на эту дугу. Как по другому можно сформулировать данную гипотезу?
Запишите теорему: вписанный угол измеряется половиной дуги, на которую он опирается. А теперь докажем её. Рассмотрим первый случай, когда сторона вписанного угла проходит через центр окружности. Перечертите рисунок первого варианта к себе в тетрадь. Угол СОD отметьте, равным х. Что нужно записать в «дано » и что нужно доказать?
|
Градусной мере дуги центрального угла СВД, т.е. 70 градусов. Градусной мере дуги центрального угла АОД, т.е. 60 градусов. Учащиеся делают вывод, что градусная мера дуги равна градусной мере центрального угла ,опирающегося на эту дугу.
У первого варианта центральный угол по условию 70 градусов, вписанный угол получили равным 35 градусам, значит вписанный угол СВД равен половине дуги СД. У второго варианта центральный угол по условию 60 градусов, вписанный угол получили равным 30 градусам, значит вписанный угол АВД равен половине дуги АД. Можно предположить, что вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности
Вписанный угол равен половине дуги, на которую он опирается.
Дано: Угол CBD – вписанный, угол COD- центральный опираются на дугу CD Доказать: Угол CBD равен половине дуги СД.
|
Учебник. |
Познавательные
|
|
|
Вспомните ход решения задачи, подсказки к задаче и докажите теорему. Ваш помощник – учебник. На самом деле вам предстоит решить задачу в общем виде. Есть ли желающие прокомментировать доказательство?
Какой пункт темы мы изучили?
Второй и третий случай рассмотрите в качестве домашнего задания. Нужно будет воспользоваться суммой и разностью градусных мер углов и применить первый случай, который мы разобрали. При необходимости можете использовать учебник стр.171.
|
1. Рассмотрим треугольник COB. Он является равнобедренным, OC= OB ( как радиусы). У равнобедренного треугольника углы при основании равны, то угол ОCВ равен углу СВО. 2. Угол COD=х - внешний угол этого треугольника. 3. По свойству внешнего угла: угол COD равен сумме двух углов треугольника, не смежных с ним, т.е. угол COD равен сумме углов ОCВ и СBО. угол COD равен сумме углов ОCВ и СBО. 4. Угол CBD равен половине угла СOD, т.е. х/2 градуса. 5. Так как градусная мера угла СОД равна градусной мере дуги СД, то вписанный угол СВД равен половине дуги СД. Теорему о вписанном угле. |
|
Познавательные
Регулятивные
Коммуникативные |
| Первичное применение нового знания 5 минут | Для закрепления теоремы решите задачу, которая предлагалась на ОГЭ в 2014 году. Четырёхугольник АВСД вписан в окружность. Угол АВС равен 560, угол САД равен 420. Найдите угол АВД.  В В
  
  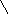 ![]() ![]() А С А С
![]() Д Д
(Ребята решают задачу в парах, учитель консультирует и делает подсказки более слабым ребятам. Представитель той пары, которая первой решила задачу, объясняет её решение у доски).
|
По теореме о вписанном угле дуга АС, соответствующая углу АВС, равна 1120 (560 умножить на 2). Дуга СД, соответствующая вписанному углу САД, равна 840 (420 умножить на 2). Тогда дуга АД равна 280 (1120 отнять 840). Следовательно, угол АВД равен 140 (280 разделить на 2). Ответ: 140
|
| Познавательные
Коммуникативные |
| Итог урока 3 минуты |
(Учитель подводит итог урока. Выставляет оценки за активную работу учащимся. ) Какая была тема на уроке? Какова была цель урока?
Достигнута ли цель урока?
Дайте определение центрального и вписанного углов.
Сформулируйте теорему о вписанном угле. |
Центральные и вписанные углы Изучить определение центрального и вписанного углов, изучить теорему о вписанном угле. Да.
Угол, вершина которого лежит в центре окружности , называется центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называют вписанным. Вписанный угол равен половине дуги, на которую он опирается.
|
|
Регулятивные |
| Домашнее задание 2 минуты | $ 2 cтр. 169 (п. 71 теорема: 1 случай –обязательно, 2 и 3-й – на выбор), № 654 ( обязательно), № 659 (на выбор). |
|
|
|





 угол
угол  В
В