Приложение 1
Выступление учащегося. Тема ««Зачем изучают логарифмы сегодня»
Мы уже знаем из предыдущего выступления что логарифмы появились в ХVI в. под влиянием все возрастающих потребностей практики как средство для упрощения вычислений. Нужны ли они сегодня, когда вычислительная техника достаточно развита, чтобы справляться с самыми сложными расчетами? Так зачем изучают логарифмы сегодня?
Испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны. Математики, выделяя самые существенные черты того или иного наблюдаемого в природе явления, вводя числовые характеристики и связывая эмпирические данные с помощью различных математических зависимостей, тем самым составляют математическую модель явления. При составлении модели того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль.
Логарифмическую спираль можно увидеть на рис.1. Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая. Так почему в качестве примера логарифмической зависимости в природе выбрали именно логарифмическую спираль?
И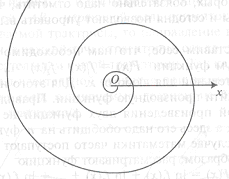
звестно, что живые существа обычно растут, сохраняя общее начертание своей формы. При этом чаще всего они растут во всех направлениях – взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с ее первоначальной формой (рис.2).
Рис.1
А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога горных козлов закручены по логарифмической спирали (рис.3).
М Рис.2
Рис.3
ожно сказать, что эта спираль является математическим символом соотношения формы и роста. Великий немецкий поэт Иоганн-Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.
По логарифмической спирали очерчены не только раковины. Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. В подсолнухе (рис.4.) семечки расположены по дугам, близким к логарифмической спирали.
П
о логарифмическим спиралям закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система (рис.5).
Л Рис.4
Рис.5
огарифмические линии в природе замечают не только математики, но и художники, например, этот вопрос чрезвычайно волновал Сальвадора Дали. И однажды, 18 декабря 1955г. Он вынес его на повестку своего публичного выступления, которое проходило в Париже, в главной аудитории Сорбонны. Сальвадор Дали рассказал о том, что происходило в Сорбонне, в своем дневнике, из которого я привожу небольшие отрывки.
«…моей навязчивой идеей, настоящей маниакальной страстью, стала картина Вермера «Кружевница», репродукция которой висела в отцовском кабинете» (рис.6).
« Рис.6-7
Уже много лет спустя я попросил в Лувре разрешение написать копию с этой картины. Потом я попросил киномеханика показать на экране репродукцию нарисованной моей копии… Я объяснил, что, пока не написал копию, в сущности, почти ничего не понимал в «Кружевнице», и мне понадобилось размышлять над этим вопросом целое лето, чтобы осознать наконец, что я инстинктивно провел на холсте строгие логарифмические кривые…» (рис.7). 
«Одновременно с этим я углубил свои исследования по морфологии подсолнуха – вопросу, по которому в свое время сделал чрезвычайно интересные выводы еще Леонардо да Винчи. Никогда еще в природе не существовало столь совершенного примера логарифмических спиралей…)
Логарифмическая спираль знаменита и своими удивительными свойствами:
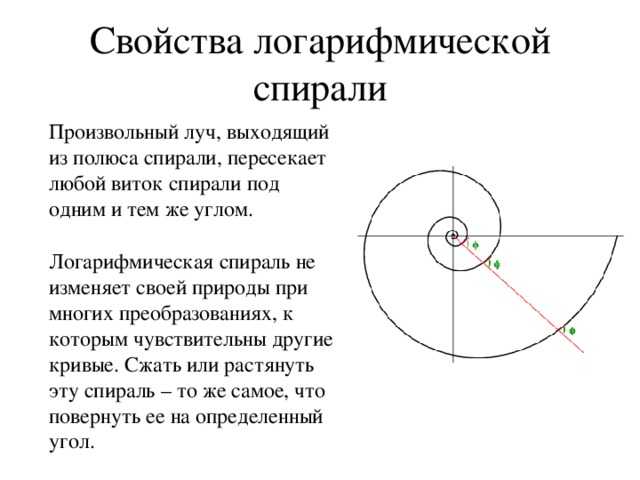
1.Она остается неизменной не только при преобразовании подобия, но и при других различных преобразованиях. Это свойство так поразило впервые изучавшего ее Якоба Бернулли (XVII в.), что он был склонен придать им мистический смысл и пожелал иметь на своей могильной плите изображение логарифмической спирали с надписью: «измененная, воскресаю прежней».
2. Логарифмическая спираль пересекает свои радиус-векторы под постоянным углом. На основании этого ее называют равноугольной.
3.Последнее свойство находит свое применение в технике. Дело в том, что в технике часто применяются вращающиеся ножи. Сила с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала.
Логарифмическая спираль – это замечательная кривая, имеющая очень много интересных свойств, но примеры логарифмической функции в природе на этом не ограничиваются. Известно, что астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины и т. д. Последовательные звездные величины воспринимаются глазом как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Получается, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов по основанию 2,5.
Практически аналогичная картина получается при оценивании громкости шума. Единицей громкости служит «бел», практически – его десятая доля, «децибел». Последовательные степени громкости 10 децибел, 20 децибел и т.д. составляют для нашего слуха арифметическую прогрессию. Физическая же «сила» этих шумов составляют геометрическую прогрессию со знаменателем 10.Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.
При оценке видимой яркости светил и при измерении громкости шума, мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения. Оказывается, что оба эти явления – следствие общего психофизического закона Вебера-Фехнера, согласно которому ощущение изменяется пропорционально логарифму раздражения. Логарифмы вторгаются и в область психологии. Теперь рассмотрим еще один интереснейший пример о связи логарифмов и музыки.
Нажимая на клавиши современного рояля, мы, можно сказать, играем на логарифмах. Действительно, так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношению к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. И основание этих логарифмов равно 2.
Это далеко не все, что можно рассказать о логарифмах. Если вас заинтересовало мое выступление дополнительные сведения можно почерпнуть в книгах Перельман Я.И. «Занимательная алгебра», Азевич А.И. « Двадцать уроков гармонии»
