ПРОЕКТ “ПІРАМІДИ ДОВКОЛА НАС»
Навчальна мета: пошукова діяльність учнів по збору інформації про поняття, види, елементи і основні властивості пірамід; активізація пізнавальної діяльності яка, у свою чергу, сприяє розвитку різносторонньої особи.
Виховна мета: виховувати в учнів прагнення до самоудосконалення, задоволення пізнавальних потреб.
Учасники: учні 11 - А класу (фізико – математичного профілю).
Вигляд проекту: творчий, практико - орієнтований;
За змістом: монопредметний;
За об'ємом: середньостроковий;
Планований результат: Створення презентаційних проектів (при захисті проекту використовуються засоби Microsoft Power Point) (комп'ютерна версія).
Робота над творчими проектами включає три етапи:
Початковий етап (визначення широкої теми, вибір робітників тим, об'єднання в групи, складання плану проектної роботи і формулювання мети, збір матеріалу).
Основний етап (аналіз способів і цілей роботи в групах, пошук джерел необхідної інформації і збір матеріалу, аналіз, можливих труднощів).
Завершальний етап (підготовка захисту готових проектів і їх захист, обговорення отриманих результатів).
Для детальнішого розгляду етапів привожу алгоритм роботи:
1 крок – визначення теми. “Піраміди довкола нас”.
2 крок – розбиття теми на дрібніші підтеми.
3 крок – формування ініціативних груп.
4 крок – збір інформації. (використання матеріалів підручн., журналів, Інтернету).
5 крок – переробка інформації і обговорення.
6 крок – систематизація і підготовка презентації, формулювання загальних висновків по темі.
7 крок – підготовка творчих звітів, презентація.
8 крок – висновок і рецензування.
Проект освоєння теми "Піраміди довкола нас"
Основна ідея
Майже п'ять тисячоліть тому єгипетський фараон і його геніальний архітектор вирішили спорудити споруду, якого ще не бачило світло – колосальну гору з каменя, побудовану за строгим математичним розрахунком, таку міцну, аби простояла до кінця століть.
Вивченням пірамід займалися багато археологів, учені, математики і кожен з них відкривав нові властивості цих споруд. До цього дня існує ще багато загадок, пов'язаних з пірамідами. Розгадати їх ще чекає майбутні покоління учених і дослідників. Все це викликало в учнів великий інтерес і спонукало їх до глибшого вивчення властивостей пірамід, як з математичної точки зору, так і з інших точок зору (історичною, географічною, в повсякденному житті).
Цілі
Познайомити учнів з поняттям піраміди, її елементами, видами пірамід.
Розвинути творчу активність учнів, уміння робити узагальнення на основі даних, отриманих в результаті досліджень.
Розвинути пізнавальну діяльність учнів, яка, у свою чергу, сприяє розвитку різносторонньої особи.
Виховувати в учнів прагнення до самоудосконалення, задоволення пізнавальних потреб.
Робочі групи і питання для дослідження
Група “Математики”
Вивчити піраміду як геометричне тіло.
Знайти визначення піраміди, які були сформульовані древніми ученими.
Порівняти сучасні трактування з древніми.
Група “Історики”
Знайти матеріали про перші піраміди.
Вивчити древні піраміди з математичної точки зору.
Сформулювати вивід про значущість пірамід з історичної і математичної точок зору.
Група “Дослідники світової системи пірамід”
Встановити наявність місць розташування пірамід на Землі.
Встановити зв'язки між місцями розташування пірамід.
Сформулювати вивід про розташування пірамід на Землі.
Група “Дослідники властивостей пірамід”
Досліджувати унікальні властивості пірамід.
Підготувати матеріал про практичне вживання властивостей пірамід.
Група “Архітектори”
Знайти матеріал, підтверджуючий вживання властивостей пірамід в архітектурі.
Підготувати ескіз будівлі з використанням властивостей пірамід і окремих її елементів.
Група “Експерти”
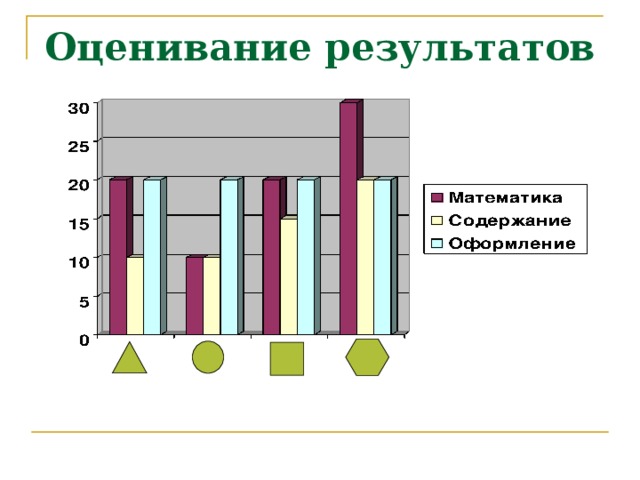
Під час звітів робочих груп стежити за їх виводами і робити свої виводи, в кінці уроку дати оцінку роботі кожної групи.
Звітні матеріали
Тип уроку: засвоєння нових знань.
Методи і прийоми роботи: реалізація проектно-дослідницької технології.
Обладнання:
Підручник геометрії для 10-11х класів, автор Погорелов А.В. та інші;
Презентація (для даної статті презентація змінена з метою зменшення інформаційного об'єму);
Малюнки;
Енциклопедичні словники;
Підручники геометрії минулих років.
Хід уроку
Вступне слово вчителя: Шановні діти! Наш урок проходить в рамках проектно-дослідницьких технологій і присвячений вже знайомому нам і в теж час загадковому геометричному тілу - піраміді. Майже 5 тисячоліть тому була споруджена перша піраміда - колосальна гора з каменя, побудована за точним математичним розрахунком. Вивченням пірамід займалися багато археологів, історики, географи. Ось і ми займемося їх вивченням не просто з дозвільної цікавості. Річ у тому, що тема “Піраміда” запланована у нас за програмою, і ми не маємо права обійти її своєю увагою. Піраміди таять в собі багато таємниць і секретів, недаремно Міхай Емінеську сказав:“А у німий далечіні застигли піраміди фараонів, саркофаги древніми були. Величаві як вічність, мовчазні як смерть”. Ці слова послужать епіграфом до нашого уроку. Сьогодні ми постараємося за допомогою ваших досліджень розкрити деякі таємниці пірамід. У підготовці до уроку брало участь 5 робочих груп:
Кожна група мала свої робочі питання, і по ходу уроку знайомитиме нас з матеріалами свого дослідження. Є у нас ще одна група - група експертів, яка уважно стежитиме за роботою на уроці і робити виводи по ходу уроку, давати свою оцінку роботі інших груп. Вас же я прошу уважно слухати своїх однокласників і записувати ключові моменти їх досліджень.
Отже, ми починаємо. Сьогодні на уроці ми повинні відповісти на одне питання: “Що є піраміда і чому вона викликає у нас такий великий інтерес?”
Слово надається групі математиків.
Перший учень. Наша група вивчала піраміду як геометричне тіло. Знайшла визначення піраміди, які були сформульовані древніми ученими, і порівняла всі формулювання, а також встановила зв'язок між розмірами пірамід і багатьма математичними поняттями. Отже, вивчивши матеріал в підручнику “Геометрія 10-11” авторів А.В. Погорелова і ін., ми узнали, що: Многогранник, складений з п-угольника А1А2А3 . Аn і п трикутників РА1А2, РА2А3 ., РАnА1 – називається пірамідою. Багатокутник А1А2А3 . Аn – підстава піраміди, а трикутники РА1А2, РА2А3 ., РАnА1 – бічні грані піраміди, Р – вершина піраміди, відрізки РА1, РА2., РАn – бічні ребра. Перпендикуляр, проведений з вершини піраміди до площини підстави, називається висотою піраміди. Площею повної поверхні піраміди називається сума площ всіх її граней.
Sполн = Sбіч + Sосн, де Sбіч – сума площ бічних граней.
Окрім довільної піраміди, існують правильна піраміда, в підставі якої правильний багатокутник і усічена піраміда.
Другий учень. Проте таке визначення піраміди існувало не завжди. Наприклад, старогрецький математик, автор теоретичних трактатів по математиці, що дійшли до нас, Евклід, піраміду визначає як тілесну фігуру, обмежену площинами, які від однієї площини сходяться до однієї точки. Але це визначення піддавалося критиці вже в давнину. Так Герон запропонував наступне визначення піраміди: “Це фігура, обмежена трикутниками, що сходяться в одній крапці і підставою якої служить багатокутник”.
Наша група, порівнявши ці визначення, прийшла до виводу про те, що в них немає чіткого формулювання поняття “основи”. Ми досліджували ці визначення і знайшли визначення Адрієна Марі Лежандра, який в 1794 році в своїй праці “Елементи геометрії” піраміду визначає так: “Піраміда – тілесна фігура, утворена трикутниками, що сходяться в одній крапці і що закінчується на різних сторонах плоскої основи”.
Нам здається, що останнє визначення дає чітке уявлення про піраміду, оскільки в нім йде мова про те, що підстава - плоске. У підручнику 19 століть фігурувало ще одне визначення піраміди: “піраміда – тілесний кут, пересічений площиною”.
І на закінчення свого повідомлення мені хочеться показати вам підручник елементарної геометрії автора Кисельова, 1907 років видання, рекомендований для середніх навчальних. У цьому підручнику наводиться визначення піраміди і її елементів (показати підручник і зачитати визначення). Це визначення перекликається з сучасним визначенням, викладеним в нашому підручнику геометрії.
Висновок експертів.
Вчитель: Арабський письменник XIII століття сказав: “Все на світі боїться часу, а час боїться пірамід”. Ці слова, як не можна, до речі. Річ у тому, що піраміди – це єдине з семи чудес світу диво, що дожило до нашого часу, до епохи телебачення і комп'ютерних технологій. Звернемося до історії виникнення пірамід і надамо слово нашим високошановним історикам.
Перший учень. Наша група, готуючись до уроку, прочитала багато енциклопедій і історичних книг. З них ми дізналися про піраміди. Читання таких книг зачаровує, ти як би потрапляєш в цю епоху епоху пірамід. Так у Великому енциклопедичному словнику написано, що піраміда - монументальна споруда, що має геометричну форму піраміди (інколи ступінчасту або башнеобразную). Пірамідами називали гробниці староєгипетських фараонів 3-го – 2-го тисячоліть до н. э., а так само постаменти храмів в Центральній і Південній Америці, пов'язані з космологічними культами (на екрані слайд єгипетських пірамід).
Другий учень. Єгипетські піраміди - прадавні з семи чудес світу, непорушно височіють на тлі жовто-коричневих пісків Лівійської пустелі. До вивчення пірамід приступили порівняно недавно. Два століття назад французький учений Жомар, що супроводжував армію Наполеона до Єгипту, склав перший науковий опис і провів перші точні виміри пірамід. Найвища піраміда – піраміда Хеопса, або Велика піраміда. В давнину її висота досягала 148 метрів. Сторона квадратної підстави дорівнює 233 метрам, а площа підстави перевищує 54 000 квадратних метрів. Загальний об'єм всієї споруди – більше 2 500 000 кубічних метрів. Складена піраміда з 2 300 000 кам'яних глиб вагою зверху 2-х тонн кожна. Глиби з усіх боків гладко відшліфовані. Це означає, що будівельникам довелося обробити близько 14 000 000 поверхонь, оскільки кожен моноліт мав 6 граней. Всі поверхні відшліфовані з такою математичною точністю, що, з'єднавши їх, між ними не можна просунути тонке лезо ножа.
Третій учень. Піраміди будували не лише в Єгипті. Вони зростали і по іншу сторону океану, в древніх державах Центральної Америки. На північ від Мехіко учені відкрили обширне місто Теотіукан, приголомшуюче пірамідами гігантських розмірів. Найбільша – піраміда Сонця, периметр її підстави рівний 1000 метрів, а напроти неї підноситься піраміда Луни (на екрані слайди із зображеннями пірамід).
Четвертий учень. Про піраміди можна розповідати нескінченно. Наша група прочитала багато книг, здавалося б, читаєш про один і той же об'єкт, але з'являються нові відомості. Систематизувавши прочитане, перед очима вимальовувалася картина, на якій змальована найдосконаліша споруда в світі.
Висновок експертів.
Вчитель: Вивчення пірамід з двох представлених точок зору не закінчується. Проводяться нові дослідження, виявляються унікальні властивості і взаємозв'язки. Слово надається третій групі – групі дослідників світової системи пірамід.
Перший учень. Наша група займалася вивченням і дослідженням світової системи пірамід. Як вже було відмічено, існують не лише єгипетські піраміди, на Землі існує ціла мережа пірамід. На тлі Гімалайського хребта чітко виділяється пірамідальна освіта - гора Кайлас (слайд); існують мексиканські піраміди. Так от, розташування м. Кайлас, єгипетських і мексиканських пірамід дуже цікаве, а саме (слайд) – якщо з'єднати м. Кайлас з мексиканськими пірамідами, то лінія, що сполучає їх, виходить на острів Пасхи. Якщо з'єднати м. Кайлас з єгипетськими пірамідами, то лінія їх з'єднання знову виходить на острів Пасхи. Обкреслилася рівно одна четверта земної кулі.
Другий учень. Продовжуючи дослідження, ми виявили, що якщо з'єднати мексиканські піраміди і єгипетські, то ми побачимо два рівні трикутники. Якщо знайти їх площі, то їх сума дорівнює одній четвертій площі земної кулі.
Якщо розглянути відстань “Кайлас - єгипетські піраміди” і “острів Пасхи – мексиканські піраміди”, то ми отримаємо рівно одну четвертую довжини лінії “Кайлас – о. Пасхи”. В результаті наших досліджень ми прийшли до виводу, що на Землі існує строга пірамідально-географічна система пірамід.
Вчитель: Спасибі учням 3-їй групи за їх унікальні дослідження. Річ у тому, що ми найчастіше чуємо про єгипетські піраміди, а не про те, що існує строга пірамідально-географічна система пірамід, усередині якої існують такі унікальні зв'язки. Але на цьому унікальні властивості пірамід не вичерпалися. Їх дослідженнями займалася 4-я група - група дослідників властивостей пірамід. Але перш ніж надати слово цій групі, давайте повернемося до групи “математиків”, оскільки їх дослідження тісно переплітаються.
Учень першої групи. Дуже часто в своїх дослідженнях учені використовують властивості пірамід з пропорціями Золотого перетину. У математичному енциклопедичному словнику дається наступне визначення Золотого перетину – це гармонійне ділення, ділення в крайньому і середньому відношенні – ділення відрізання АВ на дві частини таким чином, що велика його частина АС є середнім пропорційним між всім відрізком АВ і меншою його частиною СВ. Знаходження алгебри Золотого перетину відрізання АВ = а зводиться до вирішення рівняння а : х = х : (а – х), звідки х приблизно рівний 0,62а. Відношення х можна виразити дробами 2/3, 3/5, 5/8, 8/13, 13/21.= 0,618, де 2, 3, 5, 8, 13, 21 – числа Фібоначчі.
Учень першої групи. Геометрична побудова Золотого перетину відрізання АВ здійснюється так: у крапці У відновлюється перпендикуляр до АВ, на нім відкладають відрізок ВЕ = 1/2 АВ, сполучають А і Е, відкладають ДЕ = ВЕ і, нарешті, АС = АД, тоді виконується рівність АВ : СВ = 2 : 3.
Золотий перетин часто застосовується у витворах мистецтва, архітектура, зустрічається в природі. Яскравими прикладами є скульптура Аполлона Бельведерського, Парфенон. При будівництві Парфенону використовувалося відношення висоти будівлі до його довжини і це відношення рівне 0,618. Предмети, що оточують нас, також дають приклади Золотого перетину, наприклад, палітурки багатьох книг мають відношення ширини і довжини близьке до 0,618. Розглядаючи розташування листя на загальному стеблі рослин, можна відмітити, що між кожними двома парами листя третя розташована в місці Золотого перетину (слайди). Кожен з нас “носить” Золотий перетин з собою “в руках ” - це відношення фаланг пальців.
Перший учень четвертої групи. То, про що розповімо ми, деяким може здатися дивним і не цілком з'ясовним. Коли наша група готувалася до уроку, нами була прочитана маса науково-пізнавальної літератури, з якої ми дізналися багато що про піраміди.
При споруді єгипетських пірамід було встановлено, що квадрат, побудований на висоті піраміди, в точності дорівнює площі кожного з бічних трикутників. Це підтверджується новітніми вимірами.
Ми знаємо, що відношення між довжиною кола і її діаметром, є постійна величина, добре відома сучасним математикам, школярам – це число “Пі” = 3,1416. Але якщо скласти чотири сторони підстави піраміди Хеопса, ми отримаємо 931,22 м. Розділивши це число на подвоєну висоту піраміди (2*148,208), ми отримаємо 3,1416., тобто число “Пі”.
Отже, піраміда Хеопса – єдиний у своєму роді пам'ятник, який є матеріальним втіленням числа “Пі”, що грає важливу роль в математиці.
Ще дивніше інше співвідношення: якщо сторону підстави піраміди розділити на точну довжину роки – 365,2422 діб, то виходить 10-мільйонна доля земної півосі з великою точністю.
Я вважаю, що все вище викладене дозволяє детальніше вивчити наближені обчислення, які, чесно сказати, ми не дуже любимо і прагнемо їх уникати.
Другий учень. Вище розповідалося про Золотий перетин, так от, піраміда з пропорціями Золотого перетину в зоні своєї діяльності прямо або опосередковано виправляє структуру простору, наближає його до стану гармонії. Все, що знаходиться, або потрапляє в цей простір, починає розвиватися у напрямі гармонії. З подвоєнням висоти піраміди, її активна дія посилюється в 5 – 7 разів. Багато учених досліджували унікальні властивості піраміди з пропорціями Золотого перетину і були дуже здивовані тим, що при морозі 40 градусів усередині піраміди не замерзає звичайна вода, але при різкому струшуванні пляшки з такою водою вона замерзає за 2 – 3 секунди. Якщо дивитися на піраміду локатором в діапазоні хвиль 10 см, над нею видно іонний стовп в декілька кілометрів заввишки. Аналогічну картину дають енергоблоки атомних станцій.
Третій учень. Ми багато раз чули про поняття біблейського раю. Але його треба розглядати не в географічному сенсі, а в сенсі структури місця існування, проживання в середовищі близької до стану гармонії.
У 1997 році біля міста Осташкова на березі озера Селігер була побудована піраміда заввишки 22 метри. Дослідження води в озері показали, що вона стала набагато чистіша, ніж була раніше. Недалеко від піраміди лелека звила гніздо, що говорить про поліпшення екологічної обстановки. Уздовж русла річок відкрилися нові джерела, про які не пам'ятають навіть старожили. Аналогічні експерименти проводилися в області сільського господарства. У Дніпропетровській і Запорізькій областях були засіяні тисячі гектарів насінням соняшнику, кормового і цукрового буряка, кукурудзою, овочами, що зерновими, такими, що побували в піраміді з пропорціями Золотого перетину. Надбавка урожаю склала від 30% до 50%. В умовах засухи рослини прекрасно зростали і розвивалися.
Все вище викладене говорить про те, що піраміди, їх властивості цікаві не лише з історичної і математичної точок зору, але вони представляють інтерес і в повсякденному житті. Піраміди дозволяють вивчати незвичайні властивості предметів, умови їх розвитку і багато що інше.
Вчитель: І на завершення нашої розмови про піраміди послухаємо представників п'ятої групи – групи “архітекторів”.
Перший учень. Сьогодні на уроці ми дізналися дуже багато про піраміди. Яка історія їх виникнення, на скільки важливі їх властивості в математиці. Проте і з точки зору архітектури, і дизайнерського мистецтва піраміди представляють великий інтерес. Елементи пірамід застосовують в будівництві. Зараз це дуже модно і додає будівлі деякий шик.
Яскравим представниками в цій області є:
Торгівельний центр в Ілінге (Лондон) – зразок постмодернізму. Одна з його башт має форму піраміди і надає будівлі величавому вигляду;
Будівля книжкового ярмарку у Франкфурті (Німеччина) – дах будівлі прикрашений скляною пірамідою;
Вхід до Лувру (Париж) – це не звичайні двері, а піраміда, що зроблена із скла, має висоту 21,65 метра.
(на екрані демонструються слайди)
Другий учень. (Захищає проект будівлі, підготовлений групою)
Виведення експертної групи.
Висновок по уроку (робить учень).
Під час підготовки до уроку кожній групі довелося виконувати свою роботу, і все з'єдналося воєдино лише зараз. Мені здається, що кожен з нас отримав на сьогоднішньому уроці великий запас знань не лише з області математики, але і з області історії, географії, та і просто з довколишньої дійсності. Всі придбані знання, я сподіваюся, згодяться нам і допоможуть стати освіченішими і цікавішими співбесідниками.
Вчитель: Шановні діти. Дозвольте подякувати вам за працю, яку ви виконали, за ваші дослідження. Давайте повернемося до епіграфа нашого уроку (зачитати). Сьогодні ви прочинили завісу таємниць, які приховують піраміди. Проте вони залишаються для нас загадками. Робота кожного з вас буде оцінена індивідуально.
Література:
А.В. Погорелов. Геометрия 10-11. Киев – Освита, 2004
А.Прус. В. Швець. Прикладна спрямованість стереометрії 10-11 кл. Київ. Шкільний світ, 2007 р.
Географический атлас мира. Киев, 2005 г.
История математики в школе. Г.И. Глейзер. Москва. Просвещение – 1982 г.
Энциклопедический словарь юного географа – краеведа. Г.В. Карпов. Москва. Педагогика, 1981 г.
Энциклопедия для детей «Математика». Изд.центр «Аванта»,1998 г.
Інтернет ресурси:
http://i-math.ru/
http://www.sch57.msk.ru/collect/smogl.htm
http://pyramid.org.ua/
(Презентація учителя і роботи учнів додаються на електронному носії)