В данной работе представлена разработка контрольных мероприятий по математике 10 класс по учебнику Мордковича А.Г базовый уровень с учетом балльно- рейтинговой системой оценки знаний учащихся.. Весь курс разбит на модули. "Многогранники и тела вращения " - это тема Модуля 5. Вработе представлены вопросы к коллоквиуму( теоретическая часть ), карточка с заданиями( практическая часть) и итоговый тест( с использованием материалов ЕГЭ).
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Пример использования балльно-рейтинговой системы в преподавании математики. Модуль "Многогранники и тела вращения"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Модуль 5 Вопрсы к коллоквиуму Камалова ТИ»
Просмотр содержимого документа
«Практическая часть зачетной работы по Модулю5(многогранники) БАЗА »
Просмотр содержимого документа
«Тест по модулю Многогранники и тела вращения»
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1790 руб.
2560 руб.
2100 руб.
3000 руб.
1900 руб.
2710 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
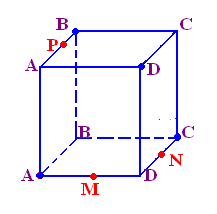 (3 балла)
(3 балла)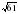 см, а радиус основания – 3 см. Найдите высоту цилиндра. (2 балла)
см, а радиус основания – 3 см. Найдите высоту цилиндра. (2 балла)