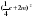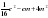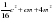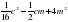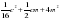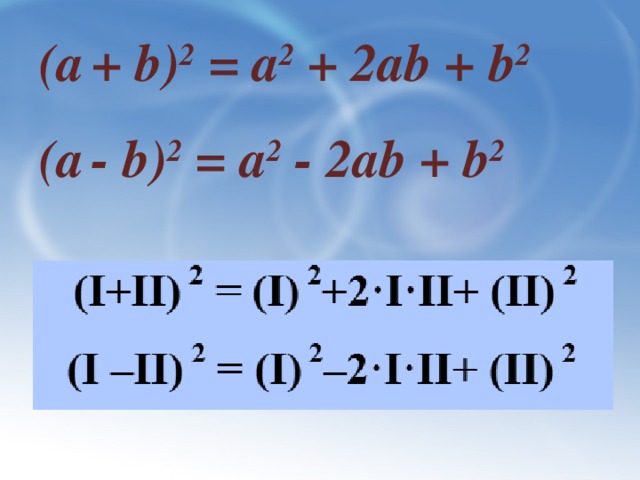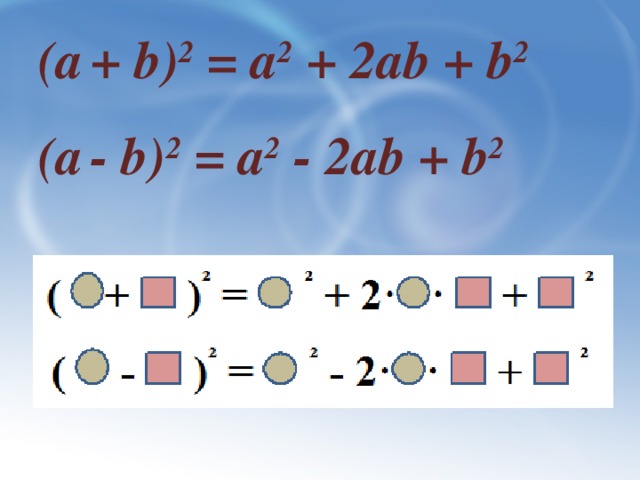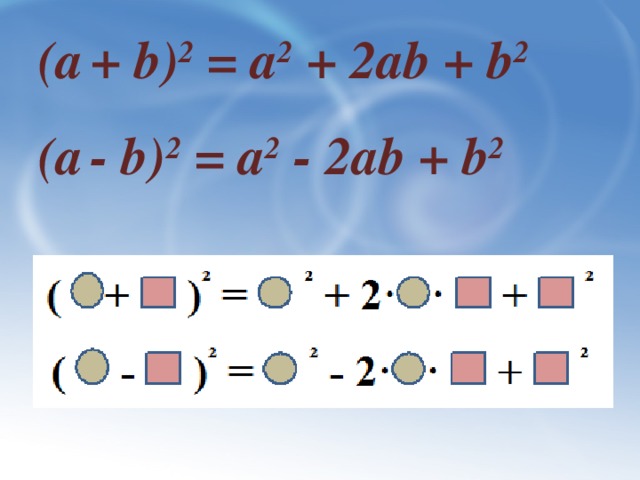ТЕМА УРОКА:
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ
Тип урока: урок изучения нового материала (задачно-проблемный)
Цели урока:
Образовательные:
-вывести формулы квадратов суммы и разности двух чисел.
-сформировать умение учащихся практически применять эти формулы для упрощения выражений.
Развивающие:
-развивать логическое мышление, внимание, память, сообразительность, культуру математической речи и культуру общения;
Воспитывающие:
-воспитывать ответственное отношение к деятельности, высокой познавательной активности и самостоятельности;
-воспитывать интерес к математике как учебному предмету через современные технологии преподавания;
- воспитывать чувство ответственности, культуры диалога, умение работать в паре, в группе.
Формы организации познавательной деятельности:
фронтальная, индивидуальная, групповая, коллективная.
Ход урока:
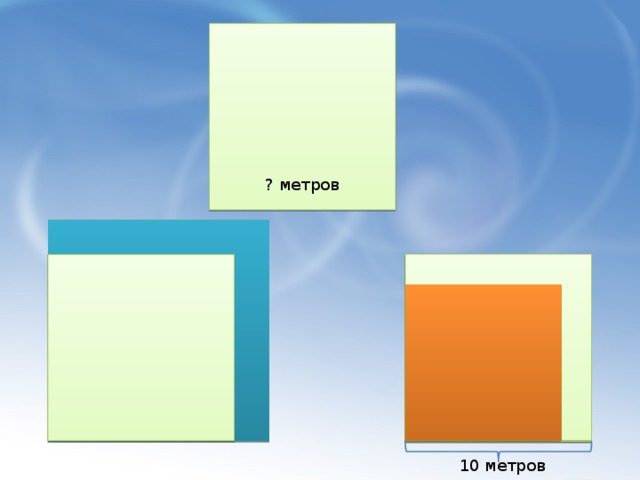
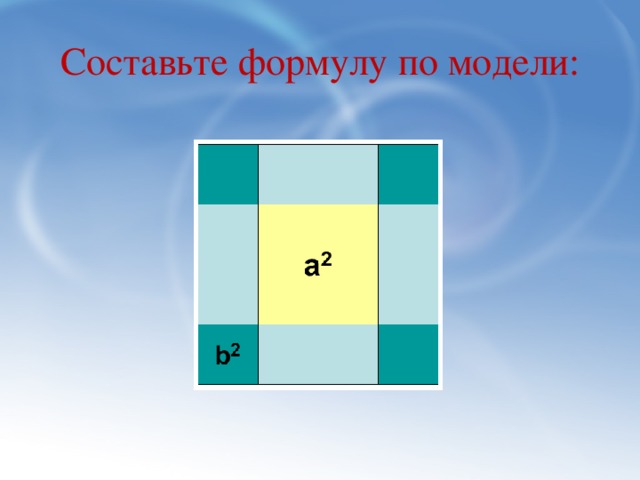
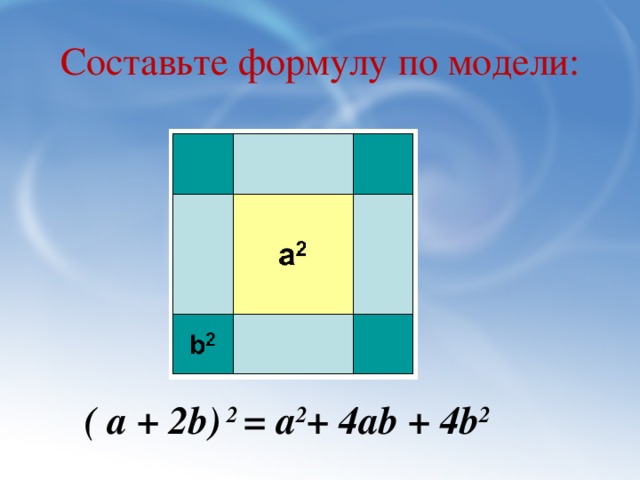
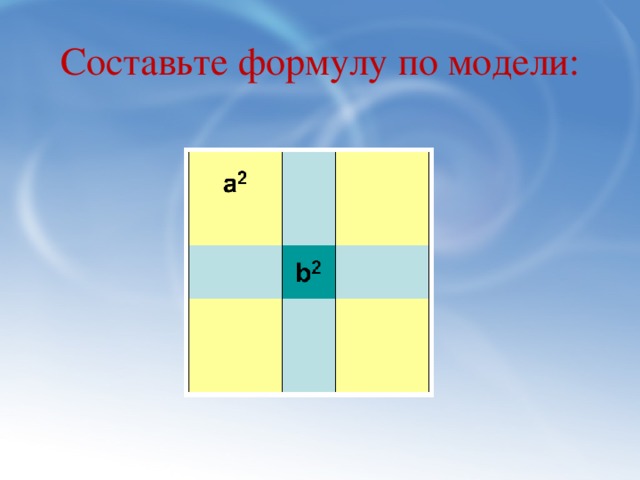
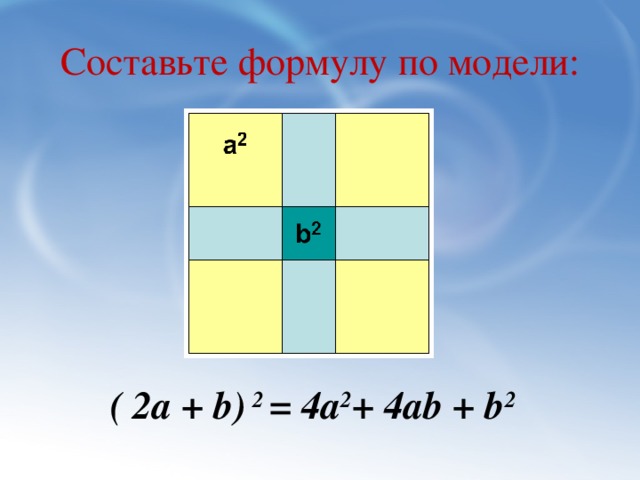
Задача: Три друга Антон, Борис и Владимир решили построить дома квадратной формы. Длина стены дома у Антона на несколько метров меньше, чем у Бориса, а у Владимира – на несколько метров больше. Выразите площадь каждого дома.
(работа в парах, время 5-7 мин.)
- Листы с решением, схемами обоих групп на доску!
Вопрсы к группам: Определитесь со своей точкой зрения! Выскажите свое мнение! Объясните свое решение? Вторая группа, вы согласны? Дети должны сами выйти на эти формулы.
а) (m+n)(m+n)= (m+n)² = m²+2mn+n²
(a+b)(a+b) = (a+b)² = a²+2ab+b².
б) (m-n)(m-n)= (m-n)² = m²-2mn+n²
(a-b)(a-b) = (a-b)² = a²-2ab+b².
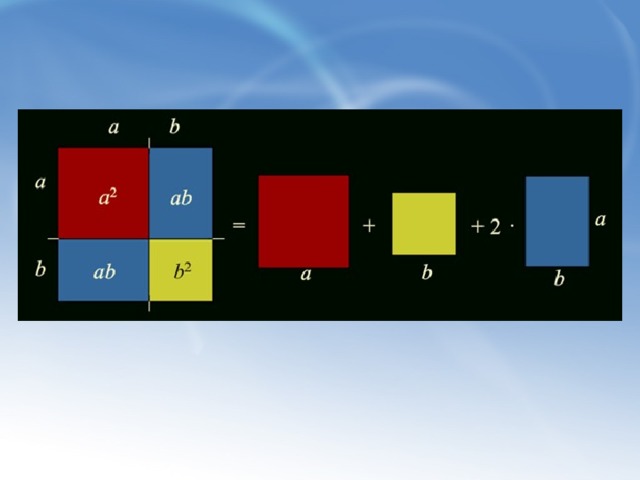
Ещё в древности было подмечено, что два одинаковых двучлена можно перемножить короче. Так появились формулы квадрат суммы (разности) двух выражений (квадрат двучлена). Эти формулы называются формулами сокращённого умножения.
Для того, чтобы учащимся было легче запомнить эти формулы, распознать их в различных заданиях можно предложить им следующую схему
( +
+ ![]() )² =
)² =  ² + 2·
² + 2· ·
·  +
+  ²
²
(I+II) 2 = (I) 2+2·I·II+ (II) 2
(I –II) 2 = (I) 2–2·I·II+ (II) 2
Учителем даётся прочтение формулы квадрат суммы, а затем учащимся даётся возможность самим сформулировать прочтение формулы квадрат разности.
Чтобы научиться преобразовывать квадрат суммы (разности) в трёхчлен с помощью формул сокращённого умножения будем придерживаться следующего плана:
Устанавливаем, что выражение является квадратом двучлена, а именно – квадратом суммы (разности);
Применяем формулу. Записываем правую часть формулы.
Приводим многочлен к стандартному виду.
(3х + 2у)² = (3х)² + 2 · 3х · 2у + (2у)²
( 3х + 2у)² = 9х² + 12х у + 4 у²
Учебник – стр.164 - работа в парах
– прочитайте правила возведения в квадрат суммы и разности двух выражений и в парах расскажите их друг другу
– разберите примеры 1 и 2 в учебнике.
Закрепление изученного материала
№ 1 (устно) Выбрать правильный ответ из предложенных.
(с + 11)2 (7у + 6)2 (2х – 3у)2
А с2 + 11с + 121 А 49у2 + 42у + 36 А 4х2 – 12ху + 9у2
В с2 – 22с + 121 В 49у2 + 84у + 36 В 4х2 – 12ху – 9у2
С с2 + 22с + 121 С 49у2 + 36 С 4х2 – 6ху + 9у2
Ответы: С, В, А.
№2. По учебнику № 803 а-г
а) (2x+3)2=(2x)2+2 2x
2x 3+32=4x2+12x+9
3+32=4x2+12x+9
b) (7y-6)2= (7y)2-2 7y
7y 6+62=49y2-84y+36
6+62=49y2-84y+36
c) (10+8k)2=102+2 8k+(8k)2=100+160k+64k2
8k+(8k)2=100+160k+64k2
d) (5y-4x)2=(5y)2-2 5y
5y 4x+(4x)2=25y2 -40уx+16x2
4x+(4x)2=25y2 -40уx+16x2
Первичный контроль.
Уровень А – карточки (приложение 1)
Уровень Б – тест на компьютере.
Д/з по уровням
Уровень А – № 799, 800, 832 Уровень Б – № 815, 816, 832.
7. Подведение итогов. Рефлексия:
- Какова была тема урока?
- Что узнали нового?
- Какие цели достигнуты?
- Какие видите перспективы при изучении темы?
- Что понравились?
- Что получилось лично у вас?
- Что можно было сделать по-другому?
Приложение 1.
1.Соедините пары так, что бы получились верные равенства
| 1. | ( 3а + с) 2 | А | y 2 – 2yв + в2 |
| 2. | ( а – 2в) 2 | Б | x2 – 2xв + в2 |
| 3. | ( x – в) 2 | В | а2 – 4ав + 4в2 |
| 4. | ( y - в) 2 | Г | 9а2 + 6ас + с2 |
2. Выбрать правильный ответ
|
| 1 | 2 | 3 | 4 |
|
| (y - 9)2 | (5x+4y)2 | (2a – 0,5x)2 | 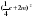
|
| а | y2 - 9y +81 | 25x2 - 20xy +16 y2 | 4a2 - 2ax +0,25 x2 | 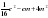
|
| б | y2 + 18y +81 | 25x2 + 40xy +16 y2 | 4a2 + 2ax +0,25 x2 | 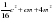
|
| в | y2 -18y +81 | 25x2 +20xy +16 y2 | 4a2 - ax +0,25 x2 | 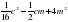
|
| г | y2 + 9y +81 | 25x2 - 40xy +16 y2 | 4a2 + ax +0,25 x2 | 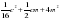
|
1.Соедините пары так, что бы получились верные равенства
| 1. | ( 3а + с) 2 | А | y 2 – 2yв + в2 |
| 2. | ( а – 2в) 2 | Б | x2 – 2xв + в2 |
| 3. | ( x – в) 2 | В | а2 – 4ав + 4в2 |
| 4. | ( y - в) 2 | Г | 9а2 + 6ас + с2 |
2. Выбрать правильный ответ
|
| 1 | 2 | 3 | 4 |
|
| (y - 9)2 | (5x+4y)2 | (2a – 0,5x)2 | 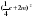
|
| а | y2 - 9y +81 | 25x2 - 20xy +16 y2 | 4a2 - 2ax +0,25 x2 | 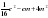
|
| б | y2 + 18y +81 | 25x2 + 40xy +16 y2 | 4a2 + 2ax +0,25 x2 | 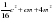
|
| в | y2 -18y +81 | 25x2 +20xy +16 y2 | 4a2 - ax +0,25 x2 | 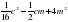
|
| г | y2 + 9y +81 | 25x2 - 40xy +16 y2 | 4a2 + ax +0,25 x2 | 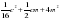
|
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
а) (2x+3)2=(2x)2 + 2.2x.3 + 32 = 4x2+12x+9
б) (7y-6)2= (7y)2- 2.7y.6 + 62 = 49y2-84y+36
в) (10+8k)2=102 + 2.8k.10 + (8k)2 = 100+160k+64k2
г) (5y-4x)2 = (5y)2- 2.5y.4x + (4x)2 = 25y2 - 40уx +16x2
| Лист достижений_______________ | Вид деятельности | Максимальное кол-во баллов | Баллы | |
|
|
| | Работа в группе | 5б |
| | Устный счет | 3б |
| | Задание по учебнику | 4б |
| | Проверочная работа | 8б |
| | Тест комп. | 8б |
| |
|
|
| |
|
|
| | Всего баллов: |
|
| Критерии: 7 – 11 баллов – «3» 12 - 15 баллов – «4» 16 - 20 баллов – «5» | 1. На уроке я работал | активно/пассивно | | 2. Своей работой на уроке я | доволен/не доволен | | 3. Урок мне показался | Коротким / длинным | | 4. За урок я | не устал / устал | | 5. Моё настроение | стало лучше / хуже | | 6. Материал урока мне | Понятен / не понятен |
|
|
| Лист достижений_______________ | Вид деятельности | Максимальное кол-во баллов | Баллы | |
|
|
| | Работа в группе | 5б |
| | Устный счет | 3б |
| | Задание по учебнику | 4б |
| | Проверочная работа | 8б |
| | Тест комп. | 8б |
| |
|
|
| |
|
|
| | Всего баллов: |
|
| Критерии: 7 – 11 баллов – «3» 12 - 15 баллов – «4» 16 - 20 баллов – «5» | 1. На уроке я работал | активно/пассивно | | 2. Своей работой на уроке я | доволен/не доволен | | 3. Урок мне показался | Коротким / длинным | | 4. За урок я | не устал / устал | | 5. Моё настроение | стало лучше / хуже | | 6. Материал урока мне | Понятен / не понятен |
|
|
|


 ·
· 
 2
2