Закончи решение уравнения: а) 1 – 6(х – 2) = 14 – 8х б) 5 (3х – 4) + 8 = 5х + 36 1 – 6х + 12 = 14 – 8х 15х – 20 + 8 = 5х + 36 8х – 6х = 14 – 12 – 1 --------------------------- - - - - - - - -- - - - - -- - 2. Реши по алгоритму следующие уравнения: а) 2 – 3(х + 2) = 5 – 2х; б) 4х – 5,5 = 5х – 3(2х – 1,5); в) 0,4х = 0,4 – 2(х + 2); г) 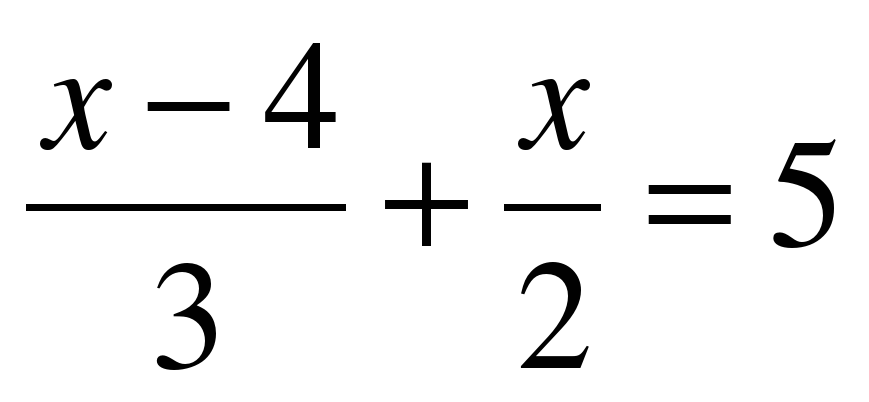 (умножь обе части уравнения на число, делящееся на каждый знаменатель); (умножь обе части уравнения на число, делящееся на каждый знаменатель); д)  ; е) ; е)  ; ж) ; ж)  3. Какое из чисел –4; 0; 14 является корнем уравнения 4х + 5 = 6 + 5(х – 3) ? 4. Реши уравнения: а) (10х – 4)(3х + 2) = 0; б) (3х + 1)(6 – 4х) = 0; в) (х + 5)(2х – 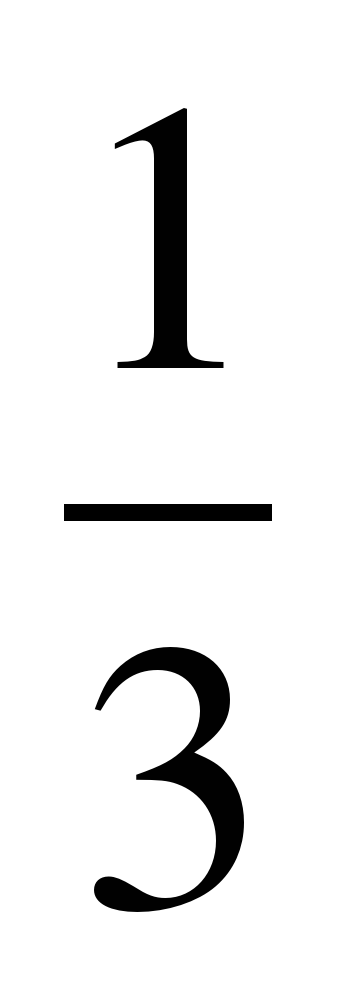 ) = 0 ) = 0 5. Какие из данных чисел являются корнями уравнения (6х + 3)(9 – х) = 0 а)  , б) 9, в) , б) 9, в) 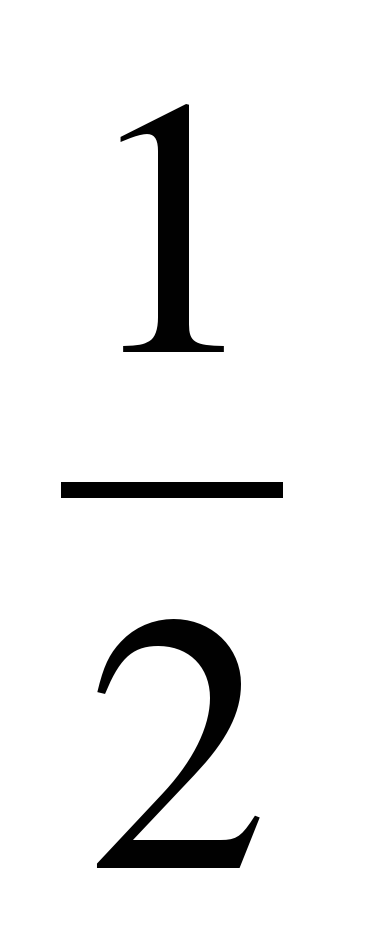 , г) – 9, д) – , г) – 9, д) – 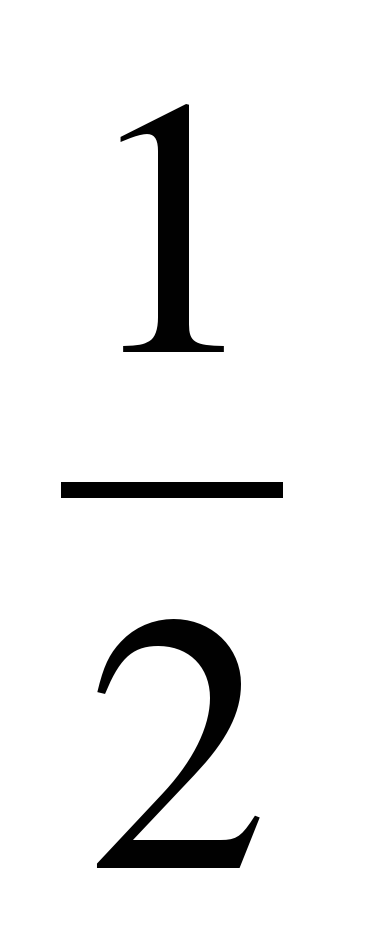 , е) – , е) –  ? ? 6. Без построения найдите абсциссу точки пересечения графиков функций: а) у = 2х + 4 и у = – 2х; б) у = 7 + 2х и у = 6х – 29
КАРТОЧКА №2: (повышенный уровень) Найди корень уравнения: а) 1,6х – (х – 2,8) = (0,2х + 1,5) – 0,7; б) 4 – 5(3х + 2,5) = 3х + 9,5; в) 4х – 5,5 = 5х – 3(2х – 1,5); г) 12 – 3(6 + 2х) = 2(2х – 9) + 2(18 + 2х); д) 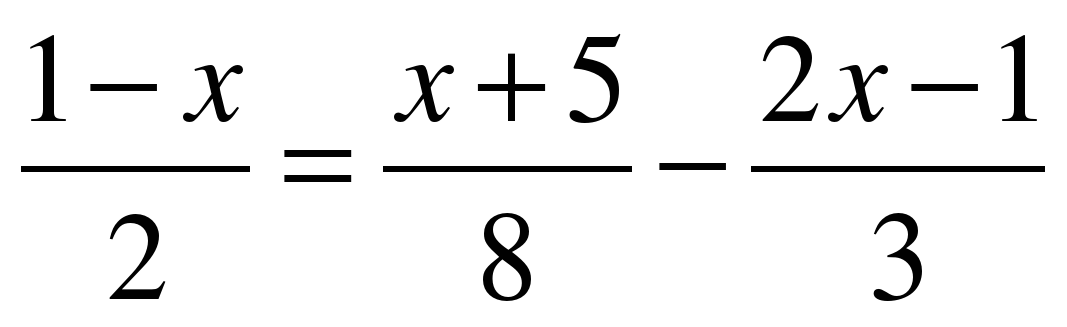 ; ; е) 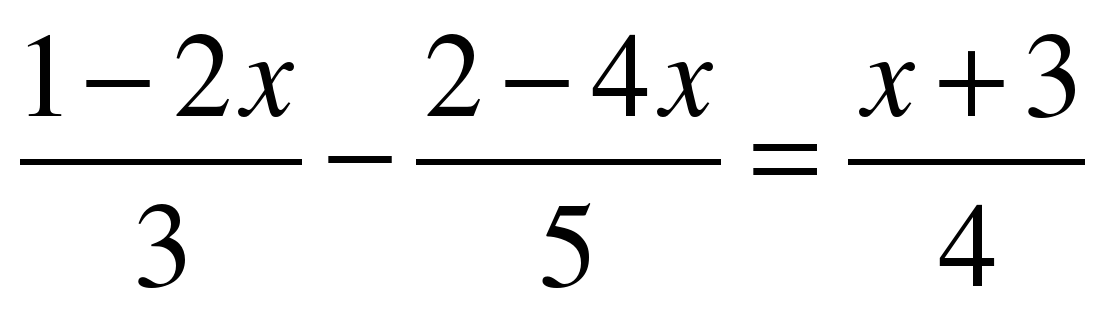 2. При каких значениях переменной х равны значения выражений: а) 6 – 4х и 3 – 5(х +1); б) 2,7m и – 3,2 + 3(2,4 – 1,1m) ? 3. Является ли корнем уравнения (2х – 3,8)(4,2 + 3х) = 0 число: а) 1,9; б) 2; в) – 1,4; г) – 3 ? 4. Имеет ли корни уравнение: а) 3х + 7 = (9 + х) + 2х; б) 5х – 1 = 4(х + 2) – (9 – х); в) х + 1 = х – 1 ? 5. При каких значениях коэффициента р уравнение рх = 10 имеет корень, равный –5; 1; 20? 6. При каком значении переменной: а) сумма выражений 2х + 7 и – х + 12 равна 14; б) разность выражений – 5у + 1 и 3у + 2 равна – 9? 7. Реши уравнение: а) 2х2 – 7х = 0; б) 3х – 7х2 = 0; в) 9х2 – 25 = 0
|