Тема: Применение различных способов для разложения многочлена на множители.
Цель: закрепить знание по указанной теме, приобретенные на предыдущих уроках; усовершенствовать умение обучающихся раскладывать многочлены на множители, используя различные способы разложения; развивать умственную деятельность, логическое мышление, слуховую и зрительную память, внимание; воспитывать положительное отношение к математике, трудолюбие, сообразительность, взаимопомощь, доброжелательность, толерантность, коллективизм, культуру общения.
Тип урока: обобщение и систематизация знаний, умений и навыков учеников
Ход урока
І. Организационный этап
Приветствие учеников. Сообщение темы урока. Проверка готовности обучающихся к уроку.
ІІ. Проверка домашнего задания
Учитель проверяет наличие выполненного домашнего задания и отвечает на вопросы учеников, которые возникли при его решении.
Работа с опережающем домашним заданием.
Вопросы к классу
1) Что называется разложением многочлена на множители?
2) Какое свойство умножения используют во время вынесения общего множителя за скобки?
3) В какой последовательности выполняется разложение многочленов на множители способом группировки?
4) Какие алгоритмы используют во время разложения на множители многочленов вида а2 – b2; a2 ± 2ab + b2; а3 ± b3?
Чтобы сделать необходимые выводы, побуждаем учеников к сравнению полученных комментариев, после чего – обобщаем выводы. (Слайд 3)
IІІ. Усвоение новых знаний
Понятно, что овладение знаниями относительно разных способов разложения многочленов на множители и умений их применять на практике является очень важным для успешного изучения многих наук. Поэтому, чтобы помочь сориентироваться ученику в безграничном пространстве разных выражений, которые раскладываются на множители, мы будем стараться дать определенный алгоритм, заметив, что он является приблизительным, то есть как и любое правило, он имеет несколько исключений.
Применение разных способов разложения многочленов на множители
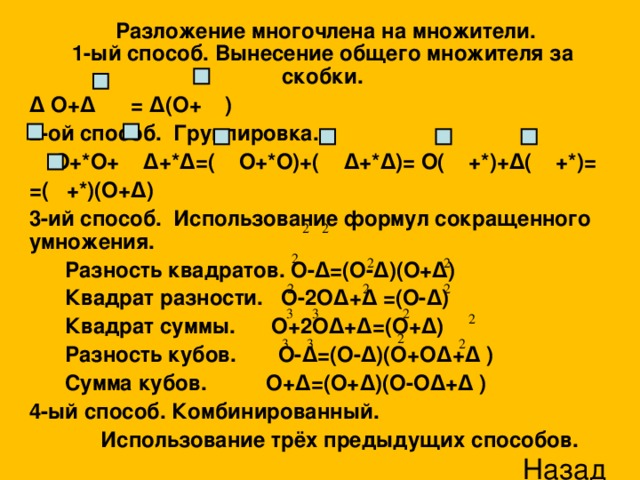
Во время разложения [применение разных способов] многочленов на множители нужно:
1) если возможно, вынести за скобки общий множитель; (Слайд 4)
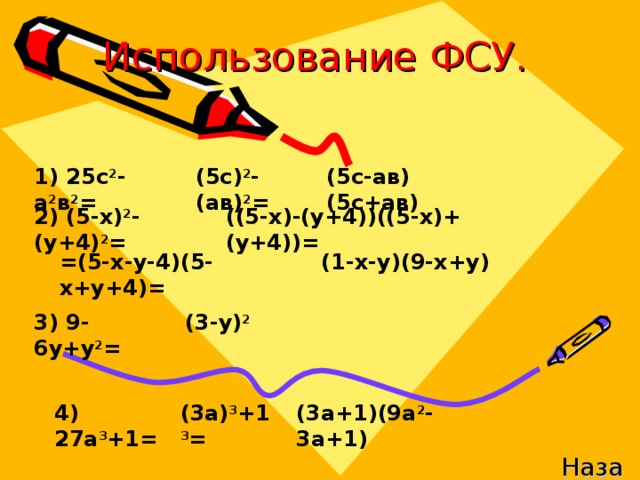
2) если общий множитель вынесен (или он отсутствует), к многочлену, который остался в скобках (или к данному), стараемся применить формулу (если это возможно); (Слайд 6)
3) если применение формулы ко всему многочлену невозможно, разбиваем его на группы (выполняем группирование). (Слайд 5)
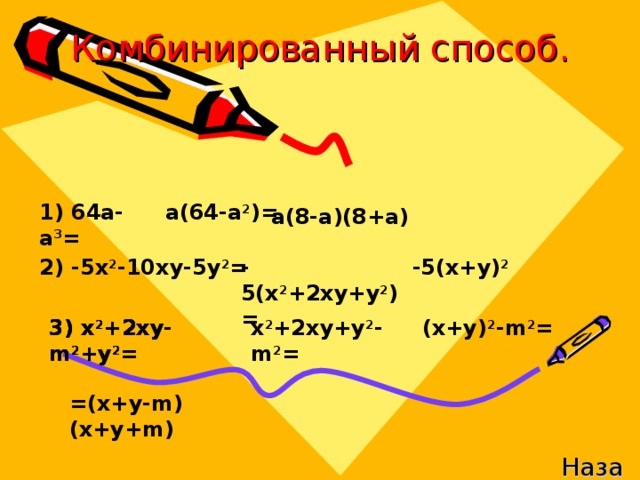
4) комбинированный способ (Слайд 7)
ІV. Усвоение умений
Выполнение письменных упражнений
Нa уроке традиционно отрабатываем применение сформулированного алгоритма и решаем соответственно упражнения на его применение.
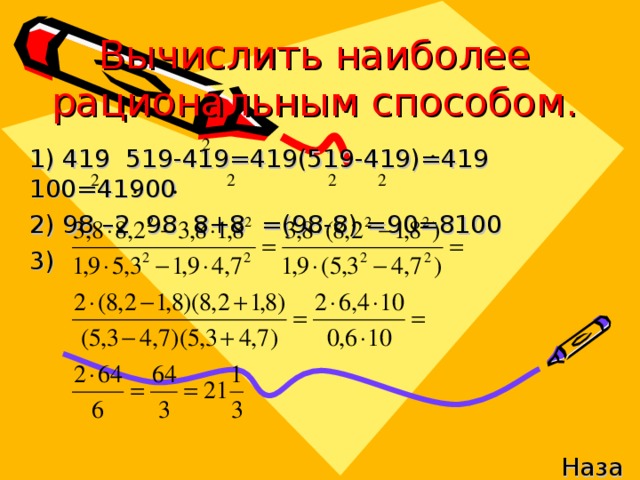
(Слайд 8-10,12)
VI. Итоги урока
В каком случае указано правильное разложение многочлена
25х2 – 25у2 на множители:
1) 25(х2 – у2); 2) (5х – 5у)(5х + 5у); 3) 25(х – у)(х + у); 4) 25(х – у)2 ?
Также для укрепления изученного материала ученикам предлагается обратить внимание на слайд 11.
VI. Домашняя задание
Используя теорию и практические навыки, полученные на уроке, выполните задания.
№ 1. Разложите на множители:
1) 14 – 14m2; 2) 3a – 3a3; 3) 7х5 – 7xy2; 4) 5x2y2 – 45а2b2;
5) 3х2 – 24ху + 48b 2; 6) -3p4 – 12p3 – 12p2; 7) 2а3 + 54b6;
8) 3х3 – 3ху – 3х2 + 3х2b; 9) 0,2х4 + 0,6х3b – 0,4х3 – 1,2х2у.
№ 2. Найдите значение выражения:
1) 3t2 + 6tp + 3p2, если t = 4,8, p = 5,2; 2) 10а2 – 10b2, если а=69, b=31.
№ 3 (опережающее). В данных выражениях (цепочках) выделите группы одночленов, чтобы они образовали выражение, которое является или полным квадратом двучлена или разностью квадратов двух выражений:
1) х2 – 2ху + b 2 – z2; 2) с2 + 9 – 6с – k2; 3) t2 + 2tp + p2 – k2;
4) a2 – 8a – b2 + 16; 5) а2 – b2 + а + b; 6) 4х2 + в – 2х – в2; 7) с2 – b2 + с – b.