| 1.Организационный момент | - Здравствуйте, ребята! Я очень рада вас всех сегодня видеть и надеюсь на совместную плодотворную работу.
Создаёт благоприятный психологический настрой на работу, организует внимание детей.
| Включаются в деловой ритм урока. |
2 | Регулятивные: организация рабочего места, прогнозирование своей деятельности Личностные: мотивация учения. Коммуникативные: Планирование учебного сотрудничества с учителем и сверстниками. |
| 2.Актуали зация опорных знаний и способов действий. | Сегодня у нас последний урок по главе «Квадратные уравнения» (Слайд 1) Это одна из самых важных тем алгебры 8 класса, т.к. с решением квадратных уравнений вы встретитесь и дальше не только в математике, но в физике и химии. Как вы думаете чем мы сегодня будем с вами заниматься на уроке? (Слайд 2). Ну что готовы? Начнем? Определяет готовность к уроку с помощью проверки выполнения домашнего задания:
- Давайте проверим домашнее задание: каждый из вас должен был решить пять уравнений. Сверим ответы. Внимание на экран! (слайд 3)
|
| Уравнения | Ответы | | 1 группа | х2 + 2х – 80 = 0 5х2 – 11х + 2 = 0 2х2 – 4х + 7 = 0 5х2 = 9х + 2 х - 5 = х2 - 25 | (-10; 8) (0,2; 2) (корней нет) (- 0,2; 2) (- 4; 5) | | 2 группа | 6х (2х +1) = 5х + 1 (х - 2)2 = 3х - 8 15х2 +17 = 15(х +1)2 (х+4)(2х-1) = х(3х +11) (2х +1)2 +2 = 2 - 6х2 | ( 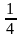 ;- ;- 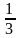 ) ) (3; 4) ( 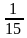 ) ) (-2) (корней нет) | - Поставьте себе столько баллов, сколько совпало ответов.
|
Формулируют задачи урока.
Проверяют и оценивают свои работы |
4 | Регулятивные: коррекция, оценка, как осознание того, что уже усвоено, умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы
Личностные: формирование позитивной самооценки
Познавательные: умение решать квадратные уравнения с помощью формул корней кв. уравнения
|
| 3.Обобще ние и закрепле ние изученного материала | 1) Устная работа - Поскольку речь у нас сегодня о квадратных уравнениях, давайте вспомним, какие уравнения называются квадратными? (Слайд 4) - Какие из уравнений будут являться квадратными? (Слайд 5) 1) -2х = 17 2) 5 - 3х = 0 3) 0,2х = -1 4) 2х2 - 18 = 3х 5) 2х + 1 = 3х -1 6) х2 - 6х +9 = 0 7) 2х2 + 8 = 0 8) 2х2 - 3х = 0 9) х3 - 4х = 0 10) х2 - 4 = 0 - Теперь проверим как вы умеете определять коэффициенты квадратного уравнения. (Слайд 6)
| Уравнение | a | b | c | | 5х2 + 5х - 3 = 0 |
|
|
| | 2х + 3х2 - 4 = 0 |
|
|
| | 3 + 4х + х2 = 0 |
|
|
| | -2х2 + х = 1 |
|
|
| | 4х2 = 4х - 1 |
|
|
|
- Я предлагаю вам поиграть, как в детстве в игру «Найди лишнее». Вам предстоит в каждой группе уравнений выбрать лишнее и объяснить свой выбор (Слайды 7 и 8)
|
| Уравнения | Ответы | | 1 группа | 2х2 + 4х – 7 = 0 9х2 – 6х + 9 = 0 5х2 – 2х = 0 7х2 + 10х - 9 = 0 |
| | 2 группа | х2 - 3х + 4 = 0 -5х2 - х + 1 = 0 х2 + 6х + 7 = 0 х2 + 5х + 12 = 0 |
|
- Теперь давайте проверим, насколько хорошо каждый из вас умеет определять виды квадратных уравнений. Вашему вниманию предлагается тест, в котором нужно определить вид пяти предлагаемых уравнений. Напротив каждого уравнения вы ставите «плюс» в той колонке, какому виду оно принадлежит (Слайд 9) 2) Тест 1 вариант | Уравнения | полное | неполное | Приведён ное | Неприве дённое | | 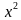 + 8х + 3=0 + 8х + 3=0
|
|
|
|
| | 6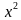 + 9= 0 + 9= 0 |
|
|
|
| | 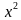 – 3х = 0 – 3х = 0
|
|
|
|
| | -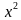 + 2х + 4 = 0 + 2х + 4 = 0 |
|
|
|
| | 3х + 6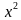 +7 = 0 +7 = 0 |
|
|
|
| 2 вариант | Уравнения | полное | неполное | Приведён ное | Неприве дённое | | 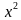 + 8х =0 + 8х =0
|
|
|
|
| | 6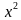 + 9 х – 7 =0 + 9 х – 7 =0 |
|
|
|
| | 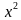 – 3х + 15= 0 – 3х + 15= 0
|
|
|
|
| | -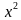 - 3х + 14 =0 - 3х + 14 =0 |
|
|
|
| | 3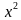 - 6х = 0 - 6х = 0 |
|
|
|
|
-Теперь обменяйтесь своими тестами с соседом по парте. Посчитайте количество правильных ответов (Слайд 10) и оцените работу своего соседа.
( Работа у доски) - Давайте вспомним как мы решали неполные квадратные уравнения Задание на доске выполняют два ученика 1) 2х2 + 7х = 0 2) х2 - 5 = 0 х2 - 16 = 0 2х2 + 18 = 0
( Алгоритм решения квадратного уравнения ) - С неполными квадратными уравнениями мы разобрались, а как решить полное квадратное уравнение? (Слайды 11 и 12)
|
Дают определение квадратного уравнения
Ответ: 4; 6; 7; 8; 10
Называют коэффициенты
1.Лишнее третье уравнение, так как оно является неполным квадратным уравнением
2.Лишнее второе уравнение, так как оно не является приведенным
Выполняют тест
Проверяют и оценивают работу своего соседа по парте
Два ученика работают у доски, остальные решают в тетрадях
Воспроизводят алгоритм решения квадратного уравнения |
4
4
5 | Познавательные: анализ, синтез, сравнение, обобщение, умение осознанно и произвольно строить математическое речевое высказывание в устной форме
Регулятивные: коррекция, планирование
Коммуникативные: выражение и аргументация своих мыслей с достаточной полнотой и точностью
Личностные: формирование готовности к самообразованию
Коммуникативные: учебное сотрудничество с учителем и сверстниками Регулятивные: коррекция, оценка выполнения задания
Личностные: формирование готовности к самообразованию
|
| 4.Релакса ция
| - Ребята, пришло время немного отдохнуть. Откиньтесь на спинку стула, опустите руки, расслабьте тело, закройте глаза... и послушайте меня ( Из истории математики ) - Ребята, вы знаете, что математика – очень древняя наука. Но уверена что, вы не знаете, когда появились первые квадратные уравнения? Их решали в Вавилоне еще до нашей эры. Но во всех найденных клинописных текстах приводятся задачи с решениями, записанные в виде рецептов, без указания каким образом найдено решение. В Европе квадратные уравнения стали известны только в 1202 году, когда итальянский ученый Леонард Фибоначи изложил формулы для решения квадратных уравнений. Правда, только в17 веке, благодаря Исааку Ньютону и Рене Декарту, формулы приняли современный вид. - Откройте глаза и посмотрите на экран (Слайд 13) где, вы увидите этих выдающихся ученых. И раз мы коснулись истории решения квадратных уравнений, то просто невозможно не вспомнить еще одного ученого математика, как вы думаете кого я имею ввиду? Франсуа Виета (Слайд14). Чем же он знаменит?.
|
Слушают учителя
Отвечают на вопрос
|
3 |
Коммуникативные: умение слушать и понимать речь других;
Коммуникативные: Умение вступать в диалог, участвовать в коллективном обсуждении вопроса |
| 5.Обобще ние и закрепле ние изученного материала. | Теорема Виета для приведенного уравнения (Слайд 15) Теорема Виета в стихах для неприведенного уравнения (Слайд 16)
7)Игра "Домино" (Слайд 17) (Ответы: (3; 4) (-16;-2) (-2;7) (-3;-2) (2;6) (-4;-1) (-1:6)
4) Работа по группам - Теорию мы повторили, но, как сказал А.В.Суворов: «Теория без практики мертва», поэтому предлагаю вам следующее задание – внимание на экран – учащимся первой группы нужно составить уравнение по его коэффициентам и решить его (Слайд18) Учащиеся второй группы вместе с учителем решают уравнение с параметром: х2 - (1 - р)х - 2р -2р2 = 0 А затем самостоятельно решают уравнение: 3х2 - 10ах + 3а2 = 0
- Ребята первой группы посмотрите на экран и проверьте свои ответы (Слайд 19)
| Формулируют теорему Виета для приведенного и неприведенного уравнений
(Ответы: (3; 4) (-16;-2) (-2;7) (-3;-2) (2;6) (-4;-1) (-1:6)
Работают в группах |
5
10 | Регулятивные: проявляют познавательную инициативу, контролирую свои действия
Познавательные: самостоятельное выполнение действий с опорой на известный алгоритм
Личностные: самооценка |
| 6.Подведение итогов. Рефлексия. | - Ребята, мы повторили все основные моменты пройденной темы, подведем итоги урока. (Слайд 20) 1) 2х² – х + 3 = 0 5) х² - 9 = 0 2) х² + 2х + 1 = 0 6) 2х2 – 5 = 0 3) х²- 5х + 6 = 0 7) 3х² - 6х = 0 4) -7х + 0,5 = 0 8) 49х² = 0 - Какие уравнения можно решить разложением на множители, выделением квадрата двучлена, извлечением квадратного корня? - Какие уравнения можно решить путем подбора? - Какие уравнения можно решить по формуле корней квадратного уравнения? Оценки я объявлю на следующем уроке, после проверки ваших работ.
(Информация о домашнем задании) - Ребята, у вас осталась не использована еще одна карточка, возьмите ее – это ваше домашнее задание (Рефлексия ) - Наш урок подходит к концу. И в завершение урока я хочу рассказать вам одну притчу. Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановил их и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?». Тот с ухмылкой ответил, что целый день возил эти проклятые камни. У второго спросил: «А что ты делал целый день?» Тот ответил: «Я добросовестно выполнял свою работу» А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма» А теперь пусть каждый из вас сам оценит свою работу на уроке. Перед вами таблица с рисунками (Слайд 21). Выберите себе тот, который, по-вашему мнению, характеризует степень участия на уроке. Кто работал как первый человек, т.е. решал весь урок эти непонятные уравнения? – 1 рисунок. Кто работал как второй человек, т.е. добросовестно решал все уравнения? – 2 рисунок. Кто работал как третий человек, т.е. приумножал свои знания? – 3 рисунок (Слайд 22.) - Спасибо за урок! Всего доброго! |
Отвечают на вопросы
Просматривают домашнее задание, если есть вопросы задают их.
Учащиеся отмечают на карточке рефлексии соответствующий рисунок
|
4
4
|
Коммуникативные: выражают свои мысли с достаточной полнотой и точностью, аргументируют свое мнение.
Личностные: проводят самооценку, учатся адекватно принимать причины успеха (неуспеха).
Регулятивные: проводят рефлексию своей деятельности.
|