Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Тип урока: Изучение, усвоение новых знаний и первичное закрепление.
Цели урока:
Обучающие:
сформировать понятие геометрической прогрессии через понятие арифметической прогрессии, используя методы сопоставления и противопоставления. Познакомить со свойствами геометрической прогрессии и формулой n-го члена. Закрепить полученные знания на примерах решения задач, в том числе из сборников ЕНТ.
КГУ «Арзамасская средняя школа»
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
9 класс
Почекаева Альбина Ивановна
Тема урока: «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»
Тип урока: Изучение, усвоение новых знаний и первичное закрепление.
Цели урока:
Обучающие:
сформировать понятие геометрической прогрессии через понятие арифметической прогрессии, используя методы сопоставления и противопоставления. Познакомить со свойствами геометрической прогрессии и формулой n-го члена. Закрепить полученные знания на примерах решения задач, в том числе из сборников ЕНТ.
Развивающие:
содействовать развитию учебно-интеллектуальных умений (сравнение, обобщение, исследовательские);
расширять эрудицию по предмету;
развивать логическое мышление, речь и внимание учащихся.
Развивать навык самооценки и взаимооценки.
Воспитательные:
создать комфортную атмосферу на уроке;
содействовать воспитанию нравственных качеств обучающихся
прививать интерес к предмету.
Тип урока: Изучение, усвоение новых знаний и первичное закрепление.
Вид урока : урок - исследование
Оборудование:
ноутбуки для работы в парах
кодоскоп и слайды для устного счёта
раздаточный материал (для каждого учащегося карта урока с заданиями)
сборники ЕНТ
познавательная выставка «Прогрессия вчера и сегодня»
Содержание урока:
Организационный момент.
Работа по повторению. Самостоятельная работа с проверкой в классе. Её цель проверить домашнее задание и создать проблемную ситуацию (задание 3).
Организация изучения понятия геометрической прогрессии и введение формулы n-го члена геометрической прогрессии (исследование - метод сравнения с арифметической прогрессией)
Первичное применение знаний и умений (закрепление изученного)
Подведение итогов работы на уроке и домашнее задание.
| Ход урока | Методы и приёмы, используемые на уроке |
| Организационный момент. Организация учащихся. Проверка готовности к уроку. Приветствие. Мотивация учащихся к активной учебной деятельности. Приветствие. Девиз урока «Терпенье и труд – всё перетрут» (Запись даты в тетрадях, темы урока)
| Приём беседы с учащимися. Приём акцентирования внимания |
| Работа по повторению и проверка домашнего задания. 1. Цифровой диктант (если утверждение верное, то вы в тетрадях ставите 9, если неверное, то ставите 1. У вас должно получиться число)
Если вы все правильно ответили, то должно получиться число 1999. Много замечательных событий произошло в нашей стране за 24 года независимости. А вот в 1999 году столица Казахстана Астана была удостоена премии ЮНЕСКО «Город мира» (вошла в список 30 лучших городов мира). Слайд 1 Коррекционная работа, если есть ошибки. Вывод: Вы хорошо усвоили определения, понимаете математическую речь на слух. В повседневном общении это очень важное качество – уметь воспринимать увиденную или услышанную информацию на и быстро принимать решение. 2. Самостоятельная работа (задания в карте урока и на слайдах ноутбука, двое учащихся решают 1 и 2 задания на крыльях доски так, чтобы ученики класса не видели решения, остальные решают самостоятельно) слайд № 2.
Самоконтроль по решению учащихся на доске 3. Изучение нового материала. 1) На мониторах слайд № 2. Обратите внимание на 3-ье задание самостоятельной работы. Каким образом вы продолжили последовательность? (путём умножения предыдущего числа на -3,). Назовите следующие два члена (следующие числа 54,-162) Слайд № 3. То есть каждый следующий член равен произведению предыдущего на некоторое одно и то же число. Такая числовая последовательность в математике называется геометрической прогрессией. 2) Теперь, работая в парах по таблице, сравниваем понятие арифметической и геометрической прогрессий, делаем выводы и основные моменты записываем в тетрадь. 3) Прочитайте определение арифметической прогрессии и сформулируйте определение геометрической прогрессии (кто затрудняется – поработайте с учебником). Какую последовательность называют геометрической прогрессией? 4) Обозначение геометрической прогрессии (запись в тетрадях) 5) Проводим далее исследование, обсуждаем в парах: может ли первый член геометрической прогрессии быть равен 0? Почему? Как называется и обозначается число, на которое умножаются члены геометрической прогрессии? (запись в тетрадях) № 204
6) Давайте выведем рекуррентную формулу (делаем всё в сравнении и записываем в тетрадях) 7) Как найти знаменатель геометрической прогрессии? 8) Используя рекуррентную формулу, можно получить формулу n-го члена. Рассмотрим геометрическую прогрессию со знаменателем q: 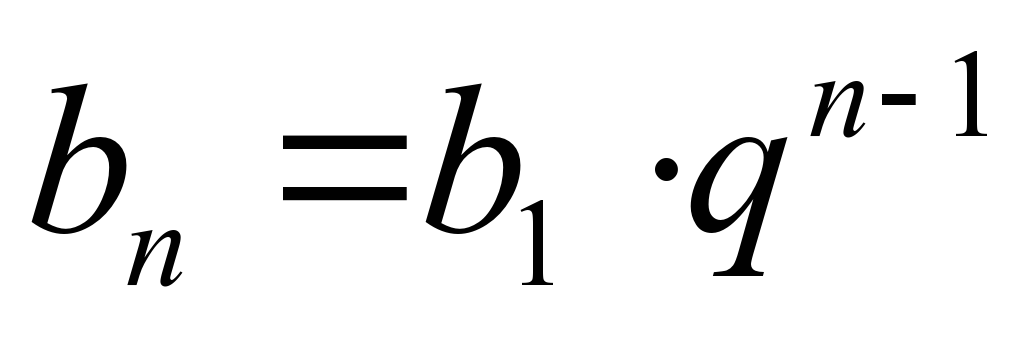8)Устный счёт (кодоскоп): в5=?; в8=?; в11=?; в20=?; в49=?; 9) Ребята, а можно ли найти в8, если известно в5 и q? Сделайте вывод. 10) Установи соответствие, отметив это в карте урока: в5 в5 : в4 q в3 . q4 в4 в1 . q4
в7 в3 . q 10) Ранее видели, что название арифметической прогрессии связано с особым свойством членов этой прогрессии. Название геометрической прогрессии также связано со свойством её членов. Поработайте с учебником (страница 71) и сделайте вывод. Итак, квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов. Извлекая квадратный корень из обеих частей этого равенства, получим, что для любых трех последовательных членов геометрической прогрессии выполняется равенство . А число, которое получилось в правой части равенства называется средним геометрическим двух чисел. Итак, запишем характеристическое свойство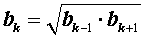
11) Устный счёт (кодоскоп) 4; ?; 36;108;… Вывод: просмотрите на ноутбуке следующие слайды, восстановите в памяти то, о чём мы с вами говорили. (слайды 4,5,6,7,8,9.)После этого перейдём к первичному решению упражнений на закрепление. Сформулируйте определение геометрической прогрессии. Почему геометрическая прогрессия названа «геометрической»? Как найти n-й член геометрической прогрессии? |
Цифровой диктант Приёмы: повторения, запоминания, активизации. Приём информационной накачки.
Метод обучения с опорой на ошибки
Приём самоконтрорля, приём оценки правильности полученного ответа
Приём создания проблемной ситуации
Приём сравнения, исследования.
Приём применения алгоритма Приём создания проблемной ситуации Приём создания проблемной ситуации
Работа с учебником
Приём применения алгоритма |
| 4. Первичное применение знаний и умений. Задача № 1. Найдите первые 5 членов геометрической прогрессии, если первый член равен -2, а знаменатель равен -0.5. (Решение пишется на доске) Ответ: -2; 1; -0,5; 0,25; - 0,125 Задача № 3. Найдите знаменатель геометрической прогрессии, если ее четвертый член 25, а шестой член 16.(можно решить тремя способами)-
Ответ: Решение задания из тестов ЕНТ.
А) 4 В) 2 С) 8 Д) 10 Е) 6 Ответ: 8 |
Приём применения алгоритмов, приём анализа результата выполнения
Тестовые задания
|
| 5. Итог урока.
Оценки за урок |
Метод «чистой доски»
Приём обобщения, прием анализа, приём |
|
Приём разноуровневых и творческих заданий |
Таблица
| Прогрессия | Aарифметическая прогрессия | Геометрическая прогрессия |
| 1. Определение. | Числовая последовательность, каждый член, которой, начиная со второго равен предшествующему члену сложенному с некоторым одним и тем же числом d , d – называется разностью арифметической прогрессии |
|
| 2. Обозначение. | (an) | ( |
| 3. Допустимые значения. | |
|
| 4. Рекуррентная формула. |
|
|
| 5. Нахождение | разности
| знаменателя |
| 6. Формула n-го члена. |
|
|
| 7. Характеристическое свойство. |
|
|
Карта урока
1 . Цифровой диктант (если утверждение верное, то вы в тетрадях ставите 9, если неверное, то ставите 1. У вас должно получиться число)
Последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же положительным числом, называется арифметической прогрессией.
Чтобы найти разность арифметической прогрессии, нужно из последующего члена вычесть предыдущий член.
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов.
Сумма натуральных чисел от 1 до 100 равна 5050.
2. Самостоятельная работа (задания в карте урока и на слайдах ноутбука, двое учащихся решают 1 и 2 задания на крыльях доски так, чтобы ученики класса не видели решения, остальные решают самостоятельно) слайд № 2.
Найдите двадцать третий член арифметической прогрессии, если первый член равен -9 и разность 4.
Найдите сумму семи первых членов арифметической прогрессии: -5;-3;-1;…
Продолжите числовую последовательность, записав еще 2 члена: -2;6;-18;…
Работа в парах по таблице, сравниваем понятие арифметической и геометрической прогрессий, делаем выводы и основные моменты записываем в тетрадь.
| Прогрессия | Aрифметическая прогрессия | Геометрическая прогрессия |
| 1. Определение. | Числовая последовательность, каждый член, которой, начиная со второго равен предшествующему члену сложенному с некоторым одним и тем же числом d , d – называется разностью арифметической прогрессии |
|
| 2. Обозначение. | (an) | ( |
| 3. Допустимые значения. | |
|
| № 204 | ||
| 4. Рекуррентная формула. |
|
|
| 5. Нахождение | разности
| знаменателя |
| 6. Формула n-го члена. |
|
|
| Устный счёт (кодоскоп): в5=?; в8=?; в11=?; в20=?; в49=?; | ||
| в5 в5 : в4 Установи соответствие. q в3 . q4 в4 в1 . q4 в7 в3 . q | ||
| 7. Характеристическое свойство. |
|
|
| Устный счёт (кодоскоп) Вставить пропущенное число: 4; ?; 36;108;… | ||
Задача № 1. Найдите первые 5 членов геометрической прогрессии, если первый член равен -2, а знаменатель равен -0.5. (Решение пишется на доске)
Задача № 3. Найдите знаменатель геометрической прогрессии, если ее четвертый член 25, а шестой член 16.(можно решить тремя способами)-
Через выражение шестого члена через четвёртый и знаменатель;
Через характеристическое свойство;
Через составление системы уравнений с двумя переменными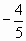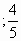
Решим первым способом.
Решение задания из тестов ЕНТ.
Второй член геометрической прогрессии равен 2. Найти произведение первых трёх членов. (Вариант 1,2011 год)
А) 4 В) 2 С) 8 Д) 10 Е) 6
В правильный треугольник, сторона которого равна 16 см, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр пятого треугольника
А) 8 В) 23 С) 12 Д) 10 Е) 16
Итог урока. Домашнее задание.
П. 12 (пример 4 рассмотреть в тетради),
№ 202 (в) – задание из уровня А
, № 207 – задание из уровня В
Творческое задание «Геометрическая прогрессия и другие науки» (Марина- информация из Интернета)
Самоанализ урока
Школа:К ГУ «Арзамасская средняя школа»
Учитель Почекаева Альбина Ивановна
Предмет: алгебра
Класс: 9 класс
Тема урока: «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»
Тип урока: Изучение, усвоение новых знаний и первичное закрепление.
Цели урока:
Обучающие:
сформировать понятие геометрической прогрессии через понятие арифметической прогрессии, используя методы сопоставления и противопоставления. Познакомить со свойствами геометрической прогрессии и формулой n-го члена. Закрепить полученные знания на примерах решения задач, в том числе из сборников ЕНТ.
Развивающие:
содействовать развитию учебно-интеллектуальных умений (сравнение, обобщение, исследовательские);
расширять эрудицию по предмету;
развивать логическое мышление, речь и внимание учащихся.
Развивать навык самооценки и взаимооценки.
Воспитательные:
создать комфортную атмосферу на уроке;
содействовать воспитанию нравственных качеств обучающихся
прививать интерес к предмету.
Тип урока: Изучение, усвоение новых знаний и первичное закрепление.
Вид урока : урок - исследование
Оборудование:
ноутбуки для работы в парах
кодоскоп и слайды для устного счёта
раздаточный материал (для каждого учащегося карта урока с заданиями)
сборники ЕНТ
познавательная выставка «Прогрессия вчера и сегодня»
Данный урок – первый по теме «Геометрическая прогрессия». Исходя из поставленных целей, наиболее эффективной формой изучения нового материала посчитала урок-исследование. Это позволило организовать активную самостоятельную деятельность учащихся по изучению новой для них темы. На основе выбранной формы урока была выстроена логическая структура урока, где каждый этап плавно переходил на следующий уровень деятельности. Урок исследование организовала таким образом, чтобы максимально активизировать учащихся на использование знаний и умений учащихся для решения проблемных заданий. С помощью карты урока учащиеся, работая в парах, сравнивают прогрессии, делают выводы. На уроке преобладают
фронтальная,
самостоятельная,
работа в парах,
Коллективная формы работы.
Все задания были направлены на развитие математической речи, на отработку алгоритмов вычисления, на запоминание правил и формул.
Применение на уроке
Ноутбуков для работы в парах
кодоскопа и слайды для устного счёта
раздаточного материала (для каждого учащегося карта урока с заданиями)
сборников ЕНТ
познавательной выставки «Прогрессия вчера и сегодня»
позволило мне организовать с учащимися активное обучение. Выполнение заданий показало, что учащиеся усвоили материал урока, владеют математической терминологией.
Для освоения учащимися темы урока на различных этапах урока применялись различные методы и приёмы обучения:
Приём беседы с учащимися. Приём акцентирования внимания
Приём самоконтроля, приём оценки правильности полученного ответа
Цифровой диктант
Приёмы: повторения, запоминания, активизации.
Приём информационной накачки.
Метод обучения с опорой на ошибки
Приём создания проблемной ситуации
Работа с учебником
Тестовые задания
Метод «чистой доски», кластер
Приём обобщения, прием анализа, приём
В течении всего урока учащимся предлагались проблемные ситуации, которые требовали реализации логического мышления. Формы деятельности на уроке от фронтальной к работе в парах, от коллективной к индивидуальной способствовали включению девятиклассников в активную мыслительную деятельность, в деятельность подготовки к ЕНТ.
Наглядные средства, ноутбуки, кодоскоп позволили насытить урок зрительными эффектами, активизировать внимание учащихся и повышение интереса к изучаемой теме и ко всему предмету. Цели, поставленные на уроке, реализованы в ходе урока.
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
)
- любые
