Открытый урок
Тема урока математики: «Тригонометрические функции, свойства, графики»
Тема урока информатики: «Построение графиков функций»
Просмотр содержимого документа
«Открытый урок Математика + Информатика "Тригонометрические функции, свойства, графики. Построение графиков функций"»
Открытый урок: Математика + Информатика
Преподаватель: Нурмухаметов Дамир Мансурьянович
,
Тема урока математики: «Тригонометрические функции, свойства, графики»
Тема урока информатики: «Построение графиков функций»
Цели урока:
Учебные
Знать свойства тригонометрических функций y = sinx, y = cosx, y = tgx, y = ctgx и уметь строить их графики.
Уметь строить графики тригонометрических функций с помощью преобразований и читать свойства функций по графикам.
Продолжить работу по формированию и развитию исследовательских навыков учащихся.
Приобретение устойчивых навыков работы при построении графиков (диаграмм) в электронных таблицах.
Воспитательные
Формировать умения:
Развивающие
Тип урока: обобщающий.
Материально-техническое оснащение урока:
учебник, компьютер, интерактивная доска
Ход урока:
Название темы
Что вы по этой теме умеете делать (Указать 2-3 пункта)
Что у вас получается плохо (Указать 1-2 пункта)
Уточняем: все ли знают изучаемую тему, как много умеют, что еще следует отработать.
Повторяем построение графика функции y= x2
Учитель:
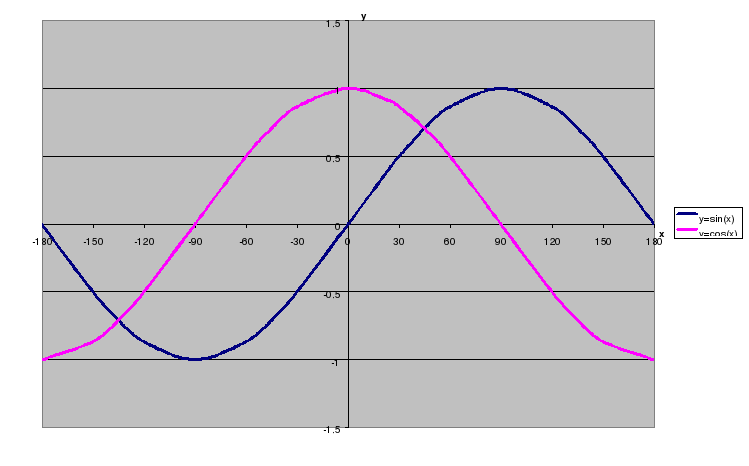
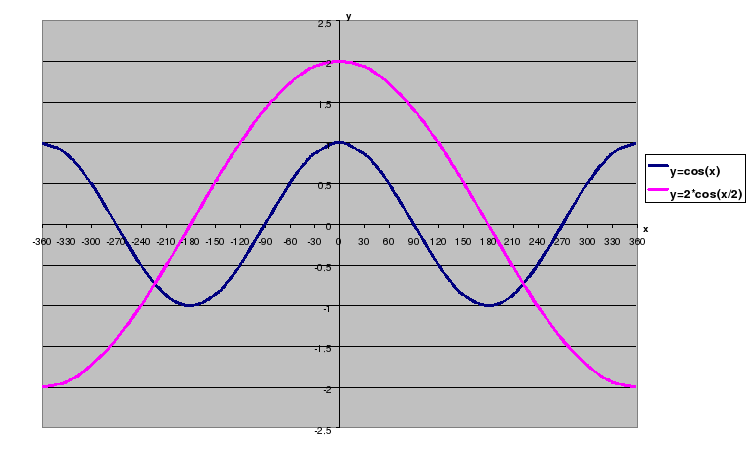
Построить в одной системе координат графики функций у=соs(x) и у=sin(x) на интервале от (-15;15) - лист №1.
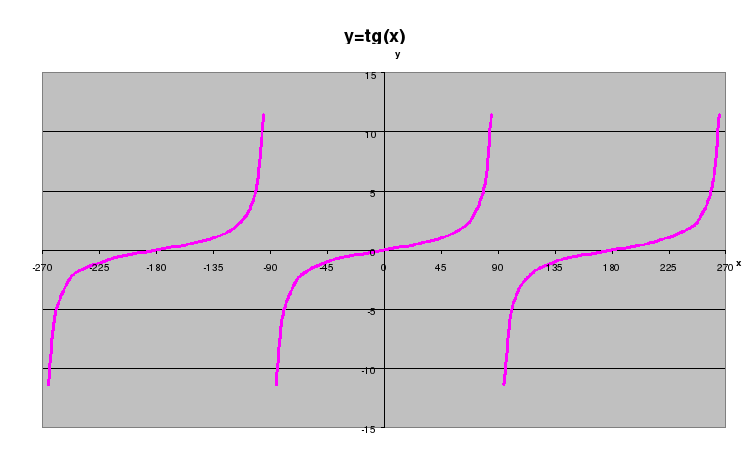
На листе №2 постройте график функции y=tg(x) (кто-нибудь из учащихся комментирует, как это делать)
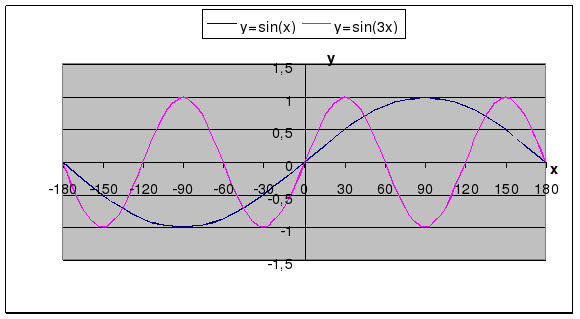
Строим графики функций y=sin3x и y=2cos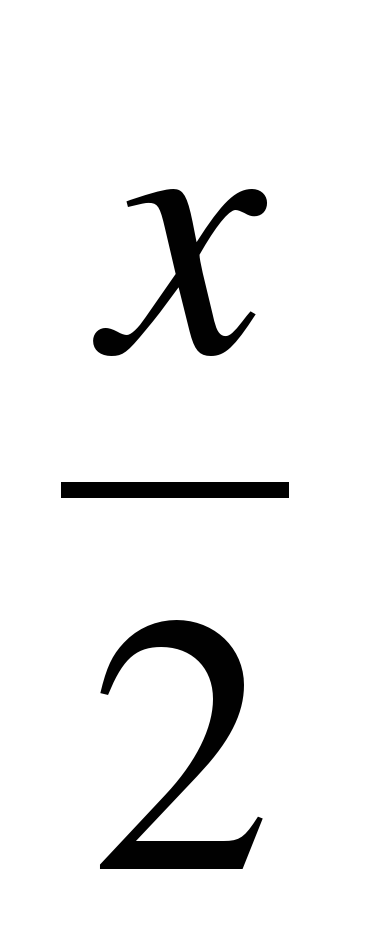 . Учащиеся, у которых возникают затруднения, строят графики вместе с учителем.
. Учащиеся, у которых возникают затруднения, строят графики вместе с учителем.
Строим график функции y = 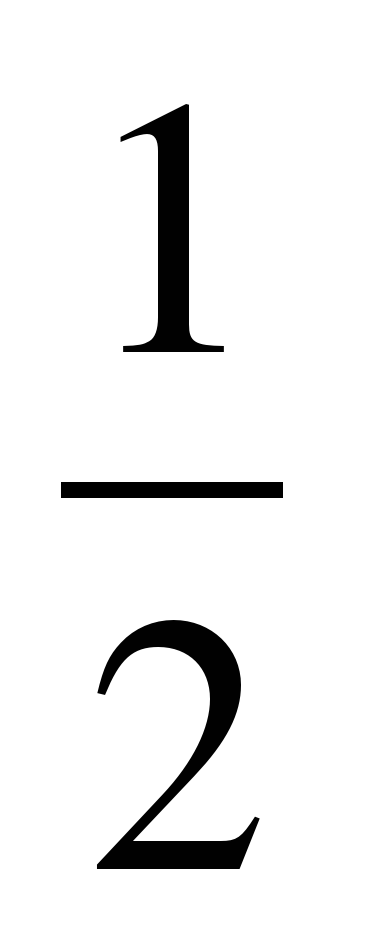 sin (2x -
sin (2x - 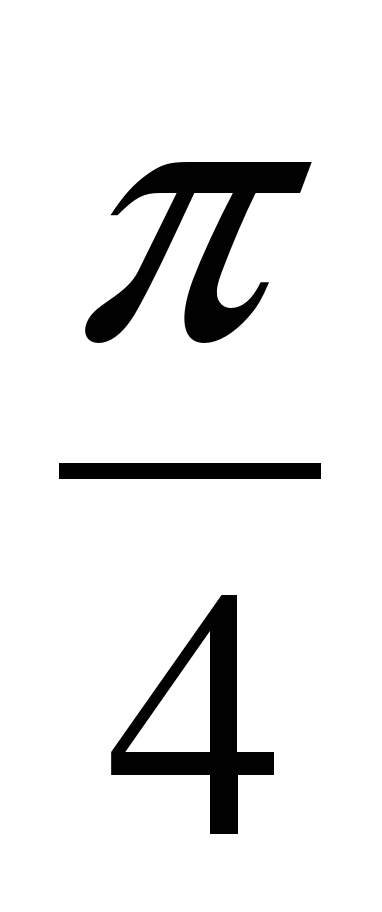 ) +
) +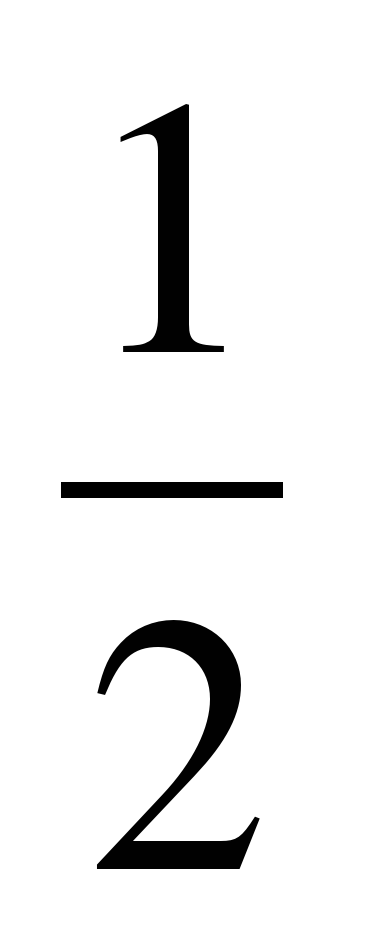 на компьютере .
на компьютере .
Может ли компьютер выявить степень трудности построения графиков 1 и 2, например, y = sinx (1) и y = 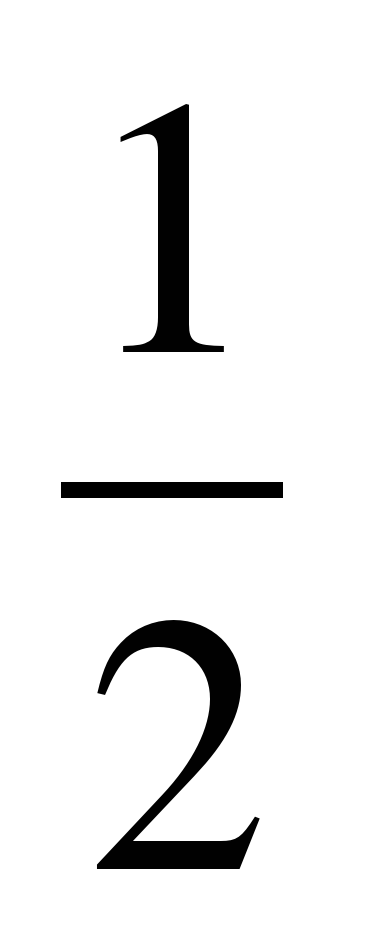 sin(2x -
sin(2x - 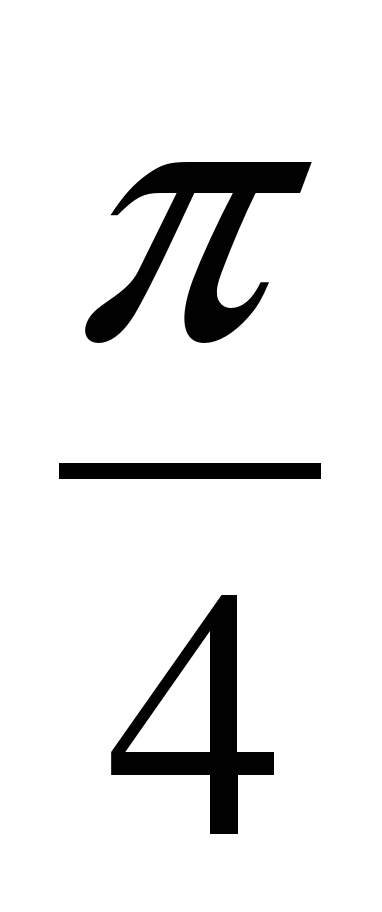 ) +
) +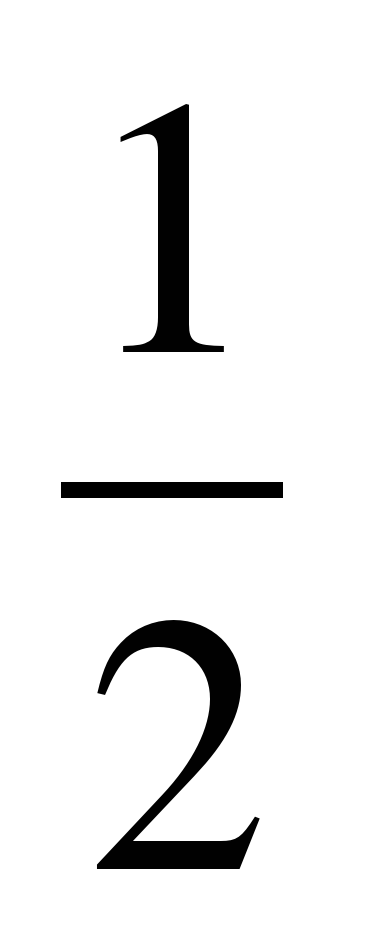 (2)? (Нет)
(2)? (Нет)
А человек? (Да)
Сколько вспомогательных графиков вы построили, чтобы построить график
функции y = 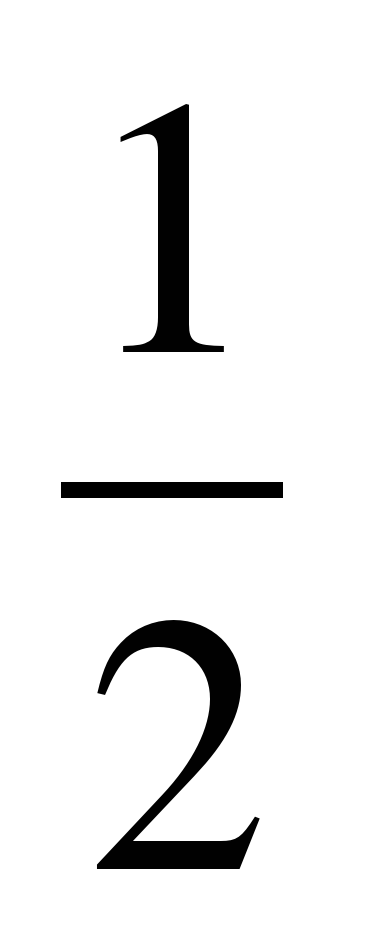 sin(2x -
sin(2x - 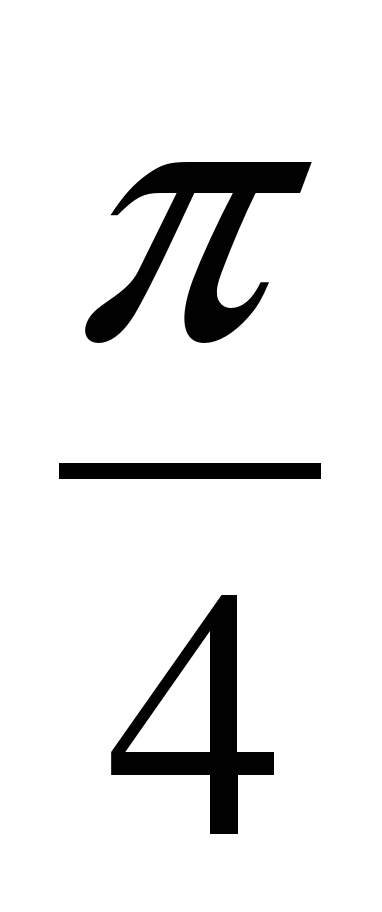 ) +
) +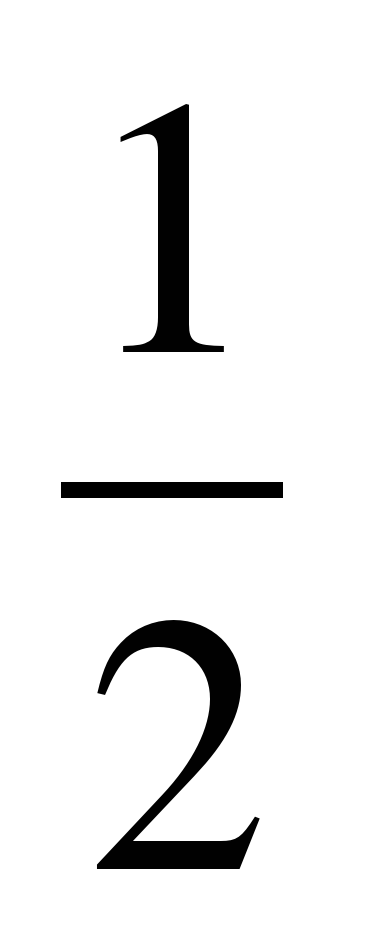 ? (Три и четвертый - искомый)
? (Три и четвертый - искомый)
В результате построения графика 2, мы будем иметь 4 графика, расположенных в одной системе координат, где нужный нам график 2 трудно просматривается.
Как избежать этого?
Строим график функции y = 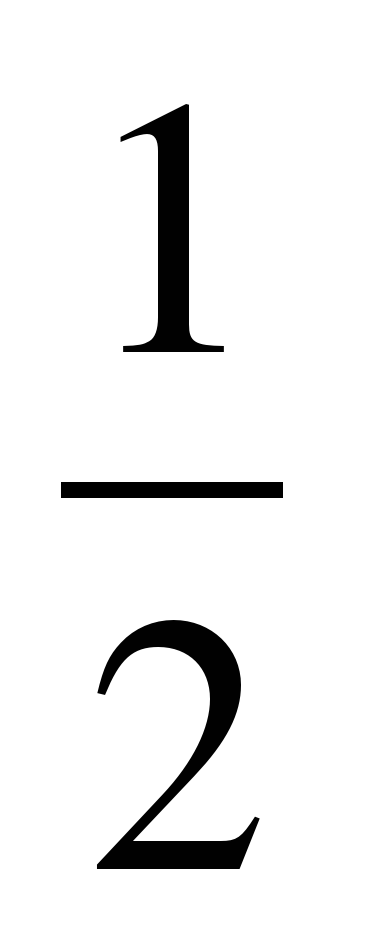 sin(2x -
sin(2x - 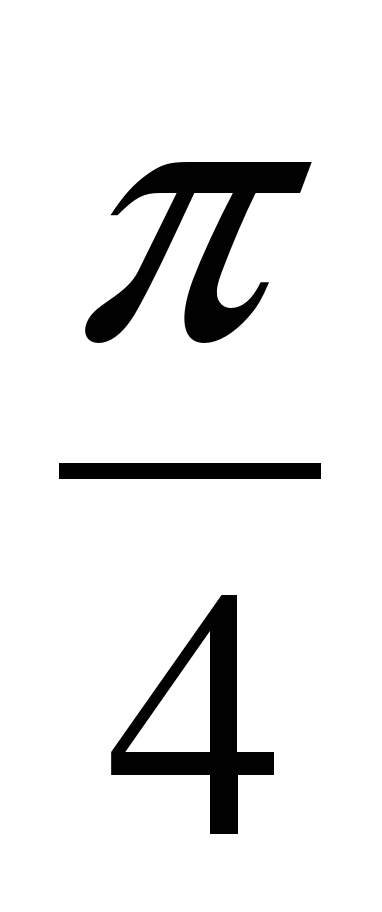 ) по алгоритму
) по алгоритму
Т0 =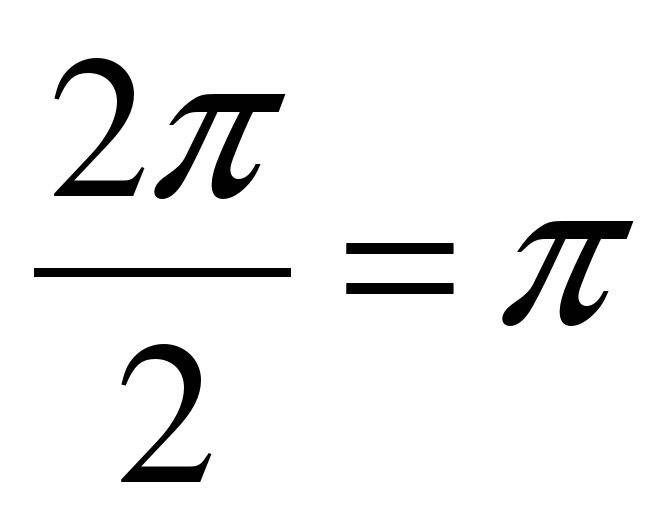
Решение:
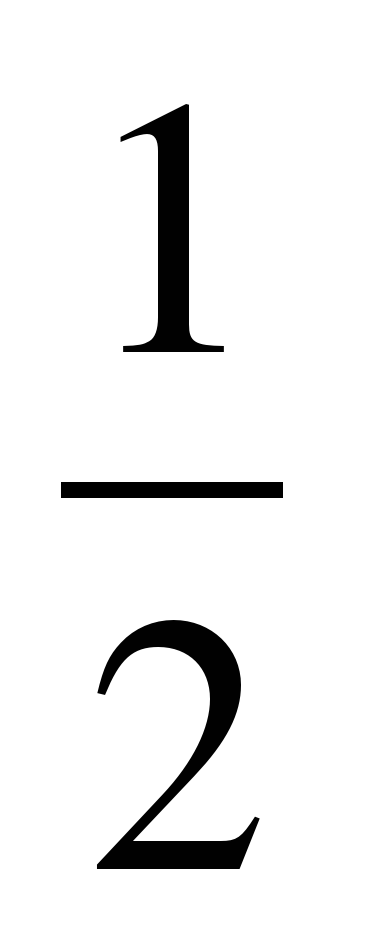 sin(2x -
sin(2x - 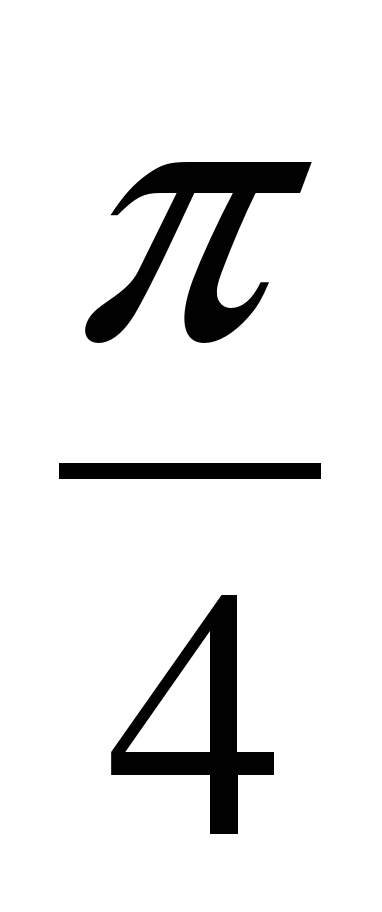 ) =
) = 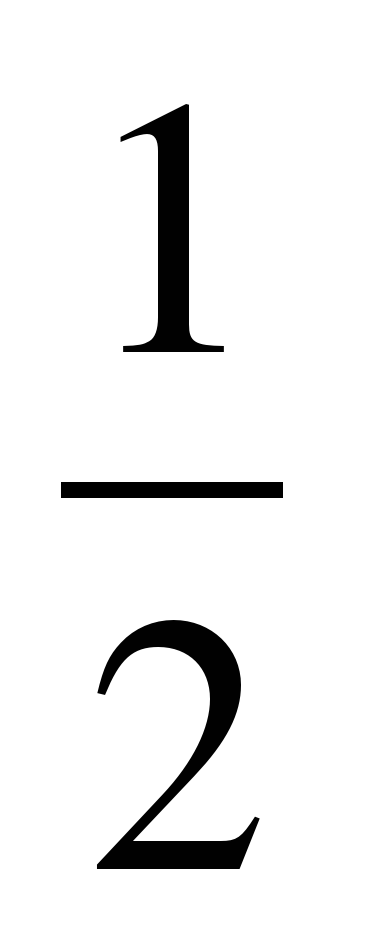 , sin(2x -
, sin(2x - 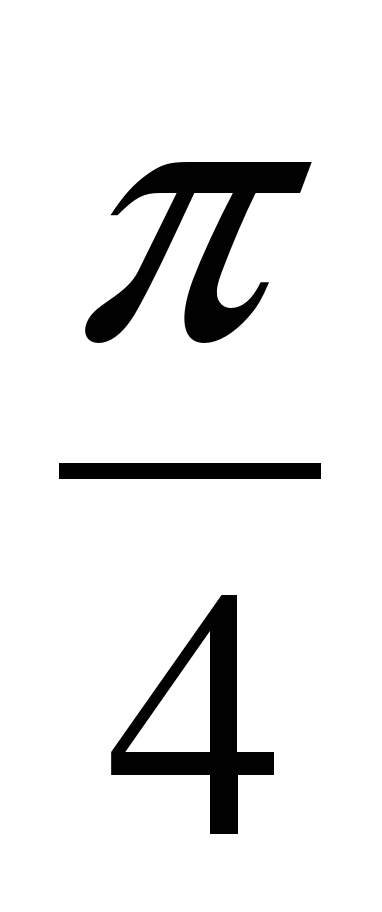 ) = 1, 2x -
) = 1, 2x - 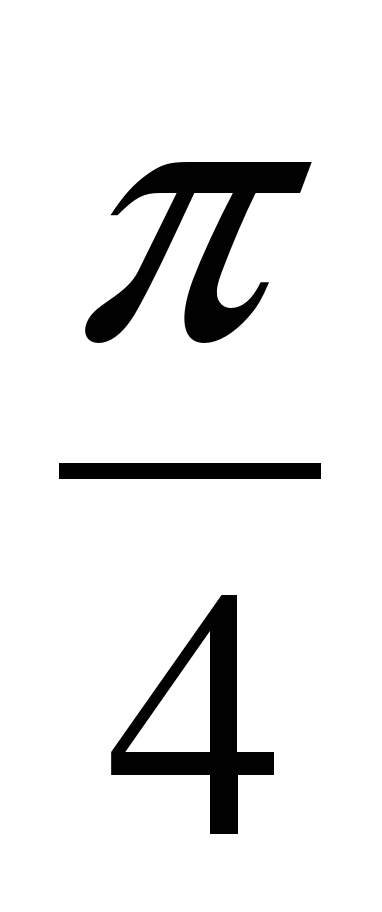 =
= 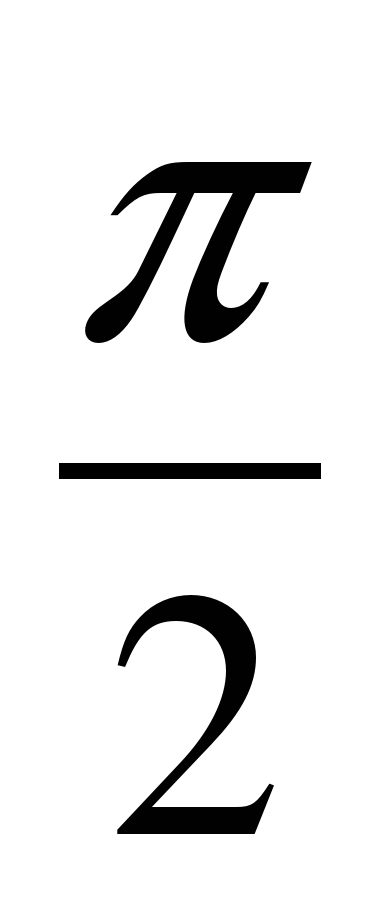 +2
+2 n, n
n, n Z, x =
Z, x = 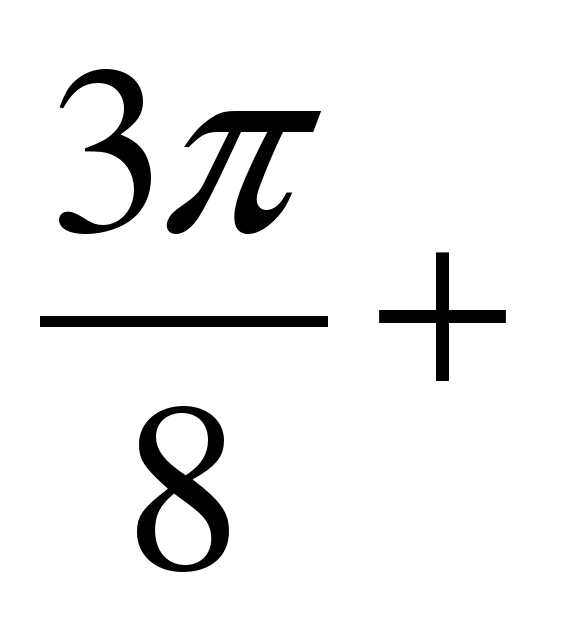
 n, n
n, n Z.
Z.
При x = 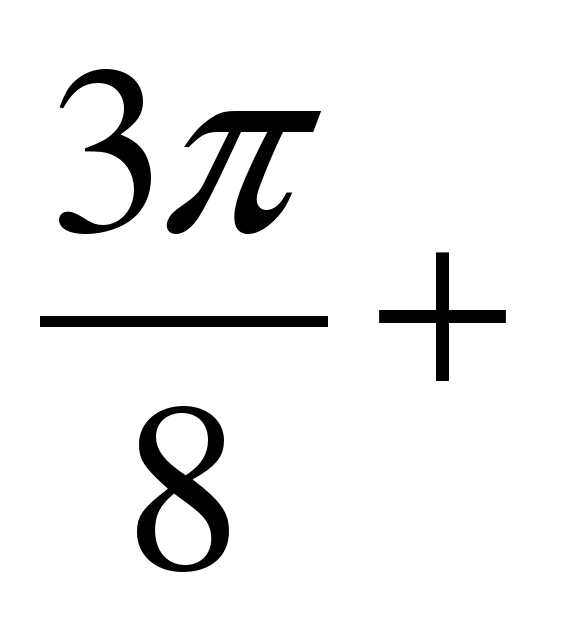
 n, n
n, n Z функция достигает наибольшее значение равное 0,5.
Z функция достигает наибольшее значение равное 0,5.
Решение:
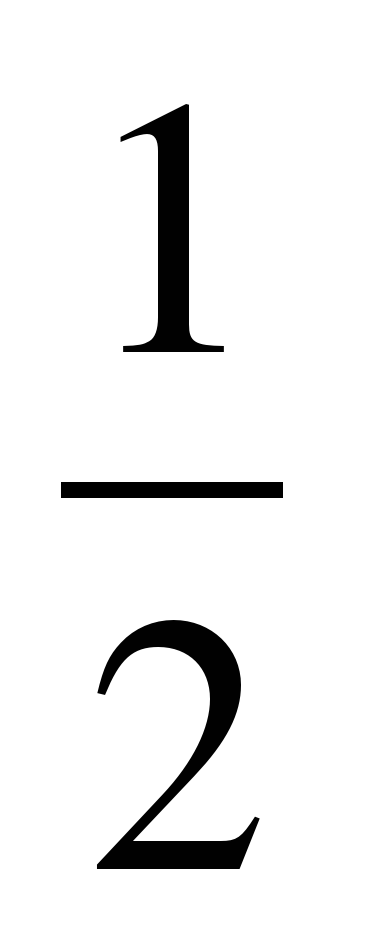 sin(2x -
sin(2x - 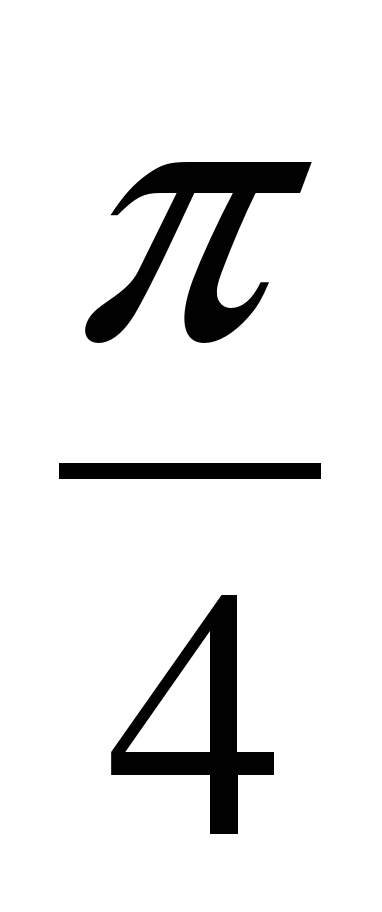 ) = -
) = - 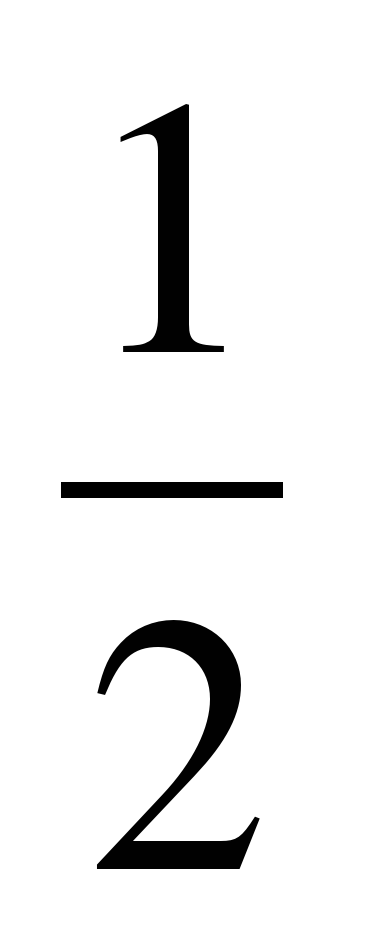 , sin (2x -
, sin (2x - 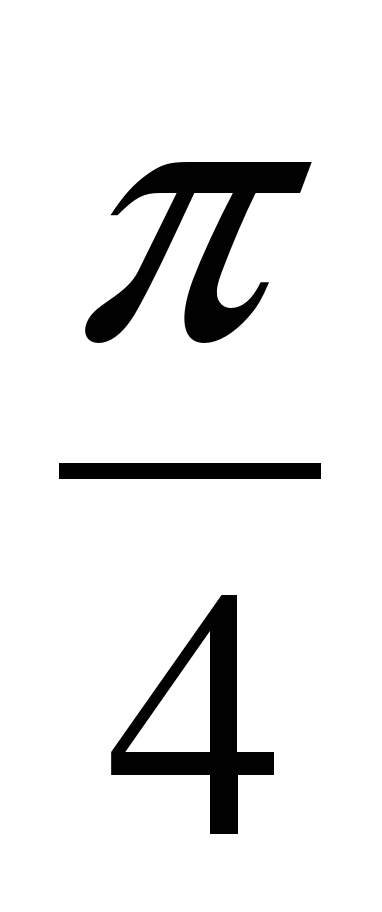 ) = - 1, 2x -
) = - 1, 2x - 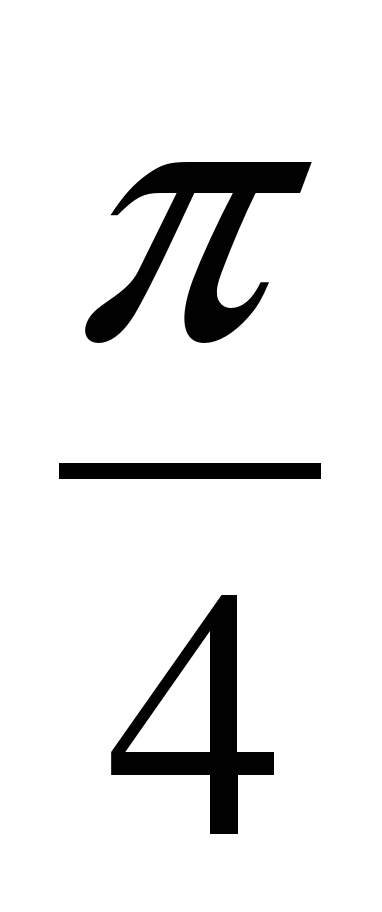 = -
= -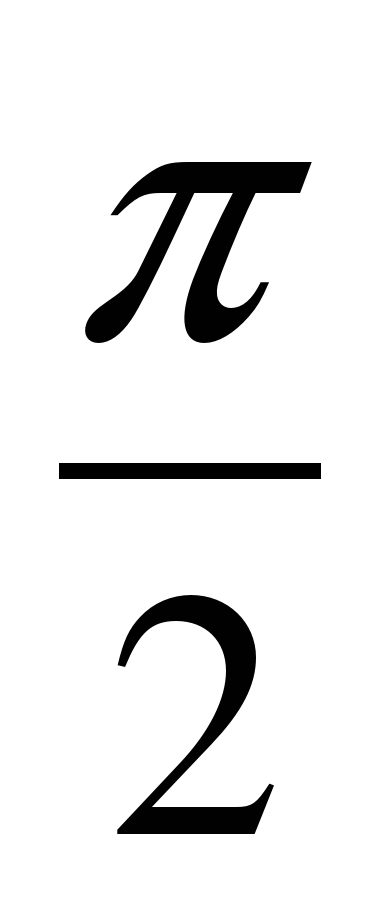 +2
+2 n, n
n, n Z, x = -
Z, x = -  n, n
n, n Z . При x=-
Z . При x=-  n,n
n,n Z функция принимает наименьшее значение равное –0,5.
Z функция принимает наименьшее значение равное –0,5.
[ -; ]. Используя периодичность функции, строим его на других интервалах.
Параллельным переносом графика функции y = 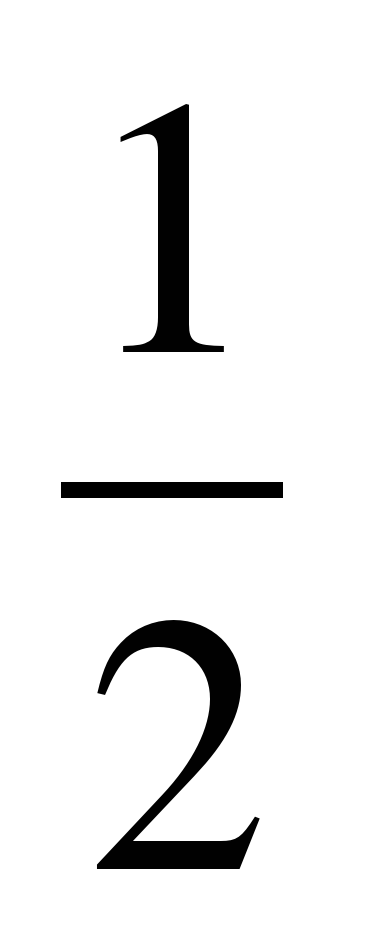 sin(2x -
sin(2x - 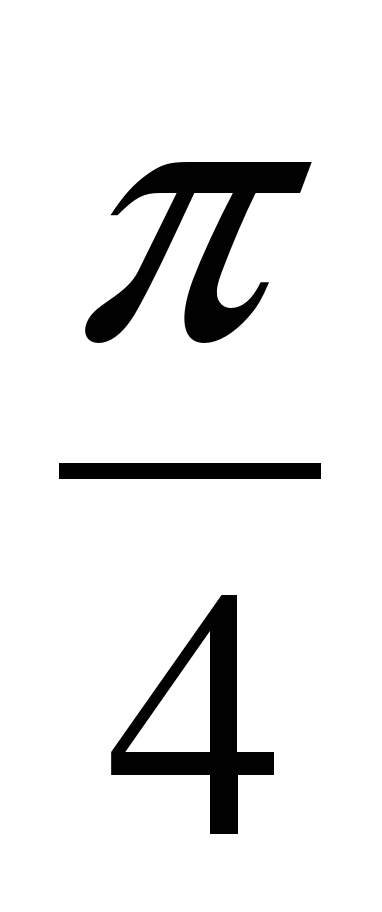 ) вдоль оси ординат на 0,5 масштабных единиц вверх, получаем график функции y =
) вдоль оси ординат на 0,5 масштабных единиц вверх, получаем график функции y = 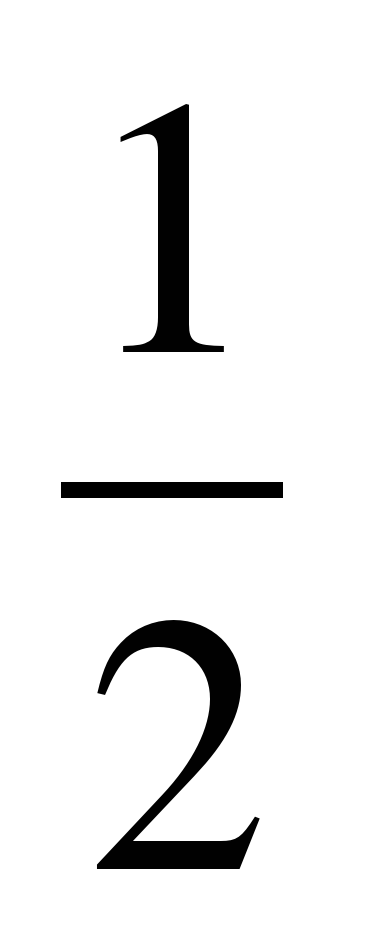 sin(2x -
sin(2x - 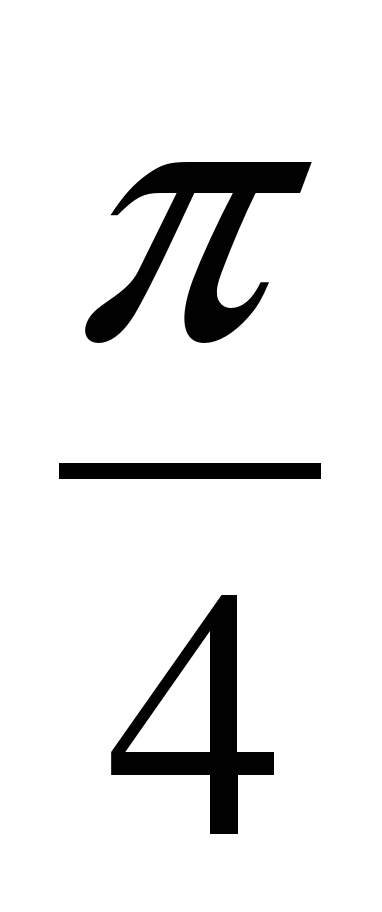 ) +
) +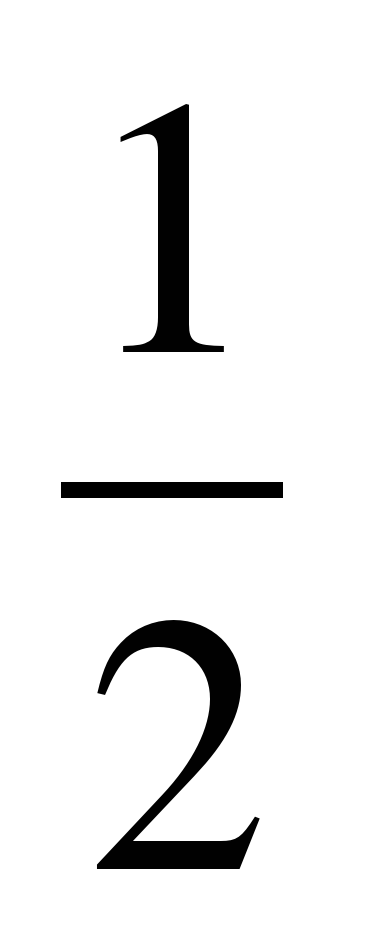 .
.
Построение графика функции y=, самостоятельно
Строим график на компьютере.
Спасибо за урок!