Ключевая средняя школа
ОТКРЫТЫЙ УРОК
Предмет: алгебра и начала анализа
Тема: Логарифмические уравнения и неравенства
Класс: 11 Б
Время реализации занятия: 1 урок (45 мин)
Учитель: Аяпбергенова Б.Т.
2012 – 2013 учебный год.
Тема: Решение логарифмических уравнений и неравенств.
Цель урока: подготовка к контрольной работе.
Задачи урока:
Образовательные: повторение теоретического материала, закрепление умения применять свойства при решении логарифмических уравнений и неравенств, обобщение приобретенных знаний.
Развивающие : развитие мышления и речи, внимания и памяти.
Воспитательные: воспитание настойчивости и упорства в достижении цели, познавательного интереса к предмету.
Тип урока: урок- обобщение
Форма урока: урок-соревнование
Оборудование: карточки для каждой группы по каждому заданию, оценочные листы, интерактивная доска, компьютер, презентация
Формы организации урока: индивидуальная, фронтальная, коллективная.
План проведения урока:
|
| Этапы урока | Временная реализация |
| 1 | Организационный момент. | 1мин |
| 2 | Разминка.
| 5 мин |
| 3 | Проверь себя. | 1,5 мин |
| 4 | Историческая справка.
| 2 мин |
| 5 | Смотри не ошибись! Дифференцированная самостоятельная работа.
| 13мин. |
| 6 | Математический поединок.
| 5 мин. |
| 7 | Логарифмическая комедия.
| 5 мин. |
| 8 | Диктант.
| 5мин. |
| 9 | Мини – экзамен.
| 5мин |
| 10 | Рефлексия | 1,5 мин |
| 11 | Подведение итогов, дом зад | 1 мин. |
Ход урока.
1. Организационный момент.
Сегодня на уроке, мы повторим теоретический материал по теме «Логарифмы» и проведем подготовку к контрольной работе.
Учащиеся класса делятся на две группы (где у каждой команды будет капитан), каждая из которых работает над определенным заданием.
2. Разминка.
Теоретический материал (устно).
1. Дайте определение логарифма числа по заданному основанию.
2. Основное логарифмическое тождество.
3. Чему равен логарифм единицы?
4. Чему равен логарифм числа по тому же основанию?
5. Чему равен логарифм произведения?
6. Чему равен логарифм частного?
7. Чему равен логарифм степени?
8. Формула логарифмического перехода от одного основания к другому основанию.
9. Какова область определения функции y=log аx?
10. Какова область значения функции y=logа x?
11. В каком случае функция является возрастающей y=logаx?
12. В каком случае функция является убывающей y=logаx?
3. Диктант: « Проверь себя»
Д. 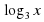 =-1
=-1
Н. lg13-lg130
О. lg8+lg125
П. 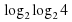
Н. 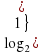
Е. 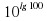
Ж. 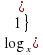 =-2
=-2
Р. 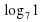
Е. 50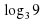
Таблица ответов. ( слайд презентации)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Д | Ж | О | Н | Н | Е | П | Е | Р |
| 1/3 | 2 | 3 | -1 | -1 | 100 | 1 | 100 | 0 |
В результате этой работы каждый ученик может оценить сам себя,
так как, если он решил правильно, то получил имя и фамилию математика-Джон Непер.
Из каждой группы выходят по 1 ученику и записывают I группа – первые 5 букв, II группа – следующие 4 буквы.
Джон Непер
4. Историческая справка.
Джону Неперу принадлежит сам термин «логарифм», который он перевел как «искусственное число». Джон Непер – шотландец. В 16 лет отправился на континент, где в течение пяти лет в различных университетах Европы изучал математику и другие науки. Затем он серьезно занимался астрономией и математикой. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI века, однако опубликовал свои таблицы только в 1614 году, после 25-летних вычислений. Они вышли под названием «Описание чудесных логарифмических таблиц».
5.Смотри не ошибись!
Дифференцированная самостоятельная работа.
Решите логарифмические уравнения:
1) 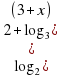 0
0
2) lg(3x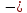 2)
2) 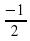 lg(x+2)=2
lg(x+2)=2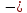 lg50
lg50
3) lg 2 x 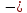 5 lgx + 6=0
5 lgx + 6=0
4) logх4 + logХ264=5
5) 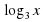 +
+ 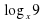 = 3
= 3
Оценка «3» - 1, 2, 3
«4» - 1, 2, 3, 4
«5» - 1, 2, 3, 4, 5
Задание выполняется под копирку; оригинал сдается учителю, а копия остается у ученика. После решения учащимся предлагается сравнить свое решение с решением на интерактивной доске. ( слайд презентации)
Решение:
1) 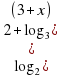 0 ОДЗ : х
0 ОДЗ : х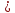 -3, 2+
-3, 2+ 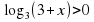
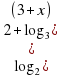
2+ 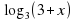 = 1
= 1
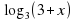 = -1
= -1
3+х= 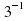
Х = - 2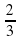
Ответ: -2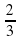
2) lg(3x-2)-1/2lg(x+2)=2-lg50 ОДЗ : 3х-2 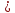 0 , х+2
0 , х+2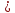 0
0
lg(3x-2)-1/2lg(x+2)= lg 100-lg50 х 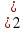 , х
, х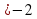
lg(3x-2)-lg 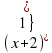 =lg2
=lg2
lg 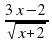 = lg2
= lg2
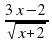 = 2
= 2
2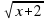 = 3х-2
= 3х-2
4(х+2)= 9х2 - 12х + 4
4х + 8 = 9х2 - 12х + 4
9х2 - 12х + 4 – 4х - 8 = 0
9х2 - 16х --4= 0 D = 400, х1= 2, х2= -2\9 - посторонний корень
Ответ: 2
3) lg 2 x-5lgx+6=0
Lg x = t t2 - 5t + 6 = 0 t1 = 2 t2= 3
Lg x = 2 lg x = 3
X= 100 x= 1000
4) 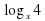 +
+ 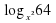 =5 ОДЗ x 0
=5 ОДЗ x 0
log x 32 = 5
x=2
Ответ: 2
5) 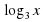 +
+ 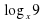 = 3 ОДЗ х 0, x
= 3 ОДЗ х 0, x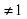
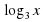 +
+ 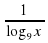 = 3
= 3
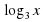 = t
= t
t+ 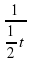 =3, t2 + 2 -3t = 0, t1 = 1, t2 = 2
=3, t2 + 2 -3t = 0, t1 = 1, t2 = 2
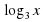 = 1
= 1 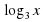 =2
=2
X= 3 x=9
Ответ: 3 и 9
6.Математический поединок.
Кто быстрее участники из команд решат свое задание.
Решите логарифмические неравенства.
1 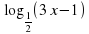 Ответ :
Ответ : 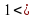 х
х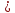 3
3
2) log3 (4x-9)х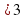
3) 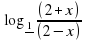
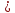
 Ответ: -2
Ответ: -2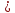 х
х
Подводятся итоги.
7. Логарифмическая комедия.
«Доказательство» неравенства 23
Рассмотрим неравенство
1/41/8
Затем сделаем следующее преобразование
(1/2)2(1/2)3
Большему числу соответствует больший логарифм, значит,
2lg 3lg
3lg
После сокращения на lg имеем: 23
имеем: 23
В чем ошибка этого доказательства?
Решение: Ошибка в том, что при сокращении на lg не был изменен знак неравенства ( на есть число отрицательное.
не был изменен знак неравенства ( на есть число отрицательное.
8. Диктант.
Вопросы – задания, на которые ученик отвечает «да» или «нет»
1. Логарифмическая функция y=log a x определена при любом х. (-)
2. Функция y=log аx логарифмическая при a0, a=0, x0. (+)
3. Область определения логарифмической функции является множество действительных чисел.(-)
4. Область значений логарифмической функции является множество действительных чисел.(+)
5. Логарифмическая функция – четная.(-)
6. Логарифмическая функция – нечетная.(-)
7. Функция y=log 3x – возрастающая.(+)
8. Функция y=logax при 0
9. Логарифмическая функция имеет экстремум в точке (1;0).(-)
10. График функции y=log ax пересекается с осью Ох.(+)
11. График логарифмической функции находится в верхней полуплоскости.(-)
12. График логарифмической функции симметричен относительно Ох.(-)
13. График логарифмической функции всегда находится в I и IV четвертях.(+)
14. График логарифмической функции всегда пересекает Ох в точке (1;0).(+)
15. Существует логарифм отрицательного числа.(-)
16. Существует логарифм дробного положительного числа.(+)
17. График логарифмической функции проходит через точку (0;0).(-)
Да(+); Нет(-)
Ответы вывешиваются на доске. Проверяют учащиеся работу соседа (работа в паре).
9. Мини – экзамен.
На этом этапе капитан каждой группы предлагает по одному заданию в карточках членам команды на свое усмотрение.
1. Решить уравнение: log 0,5 (x -7)=-1
2. Найдите область определения функции: f(x)=log 0,9 (3x-2) + log 0,9 (5-2x)
3. Решите неравенство: log 0,4(-x)
4. Решите неравенство: log 4(x-2)
5. Решите уравнение: lg 2x-lgx=0
Ответы: 1) 9; 2) (2/3; 5/2); 3) (-∞ ; -1); 4) (2; 18); 5) 1; 10
Решения сдаются учителю.
10. Рефлексия
Задайте формулой любую логарифмическую функцию и запишите на листочке одним из следующих цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работы
Красный - отличное
Зеленый - хорошее
Синий – удовлетворительное
11. Подведение итогов урока.
Учитель отмечает работу каждой команды, капитанов.
12. Домашнее задание : Подготовиться к контрольной работе
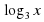
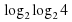
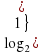
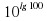
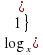 =-2
=-2 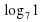
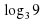
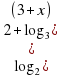 0
0 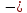 2)
2) 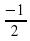 lg(x+2)=2
lg(x+2)=2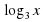 +
+ 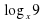 = 3
= 3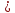 -3, 2+
-3, 2+ 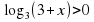
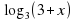 = 1
= 1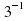
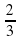
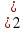 , х
, х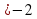
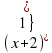 =lg2
=lg2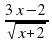 = lg2
= lg2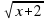 = 3х-2
= 3х-2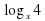 +
+ 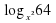 =5
=5 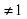
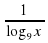 = 3
= 3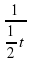 =3, t
=3, t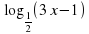 Ответ :
Ответ : 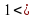 х
х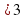
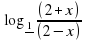







 0, log 3 ( 3+x)= -1 2+log 3 (3+x) 0 3+x= 1\3 x= -2 2\3 Ответ: -2 2\3" width="640"
0, log 3 ( 3+x)= -1 2+log 3 (3+x) 0 3+x= 1\3 x= -2 2\3 Ответ: -2 2\3" width="640"
 0, x+20 Ответ: 2" width="640"
0, x+20 Ответ: 2" width="640"
 0, Ответ: 100, 1000." width="640"
0, Ответ: 100, 1000." width="640"
 0, X ≠1 Ответ:2." width="640"
0, X ≠1 Ответ:2." width="640"
 0 log 3 x + 1\log 9 x =3 log 3 x + 2\log 3 x =3 log 3 x = t t+ 2\t – 3 = 0 /· t t 2 + 2 -3t = 0, t 1 = 1, t 2 = 2 log 3 x =2 log 3 x = 1 x= 9 x=3 Ответ: 3 и 9" width="640"
0 log 3 x + 1\log 9 x =3 log 3 x + 2\log 3 x =3 log 3 x = t t+ 2\t – 3 = 0 /· t t 2 + 2 -3t = 0, t 1 = 1, t 2 = 2 log 3 x =2 log 3 x = 1 x= 9 x=3 Ответ: 3 и 9" width="640"
 log 1/π 2" width="640"
log 1/π 2" width="640"


















