Учитель математики средней школы №6
Белгибаева Неля Борисовна.
Урок-закрепление в 5 классе на тему:
«Решение примеров на нахождение наибольшего общего делителя и наименьшего общего кратного»
Цели:
-отработать умения и навыки решения заданий и примеров на нахождение наибольшего общего делителя и наименьшего общего кратного,систематизировать, расширить и углубить знания и умения учащихся применять свойства НОДа и НОКа в решении задач, способствовать развитию наблюдательности, умению анализировать, сравнивать, делать выводы, побуждать учеников к само- и взаимоконтролю, вызывать у них потребность в обосновании своих высказываний, закрепить правила нахождения и вычисления НОДа и НОКа, сформировать навыки вычислительных задач, обогатить математический язык и расширить кругозор.
-развитие логического мышления; развитие интеллекта через заучивание математических терминов; развитие навыков самоорганизации; развитие воли через задание посильной сложности.
-воспитывать привитие интереса к математике, аккуратность записей; воспитывать уважительное отношение друг к другу.
Ход урока.
1.Организационный момент.
1 препятствие.
Математика – царица наук,
Арифметика – царица математики
(К.Гаусс)
1. Дайте определение натуральных чисел.
2.Какое число называется простым числом?
3.Назовите все простые числа до 30.
4.Какое число называется составным числом.
5.Назовите все составные числа до 20.
6.Что значит разложить натуральное число на простые множители?
7.Какое число называется наибольшим общим делителем двух натуральных чисел?
8.Какие числа называются взаимно простыми?
9.Как найти наибольший общий делитель нескольких натуральных чисел?
10.Как обозначается наибольший общий делитель?
11.Какое число называют наименьшим общим кратным двух натуральных чисел?
12.Как обозначается наименьшее общее кратное?
13.Как найти наименьшее общее кратное двух или нескольких натуральных чисел?
2 препятствие.
Тот, кто не знает математики, не может узнать никакой другой науки.
(Роджер Бэкон)
Вы любите сказки?Тогда мы побываем в гостях у сказки «Курочка - Ряба»
1)Жили – были дед и баба. Была у них курочка – Ряба. Курочка несет каждое второе яичко простое, а каждое третье золотое. Может ли такое быть?
2)Маленькая коробочка вмещает шесть яиц, а большая – десять яиц. Найдите наименьшее число яиц, которое может быть разложено как в маленькие коробки, так и в большие?
Ответы:
1.Нет, так как шестое яичко будет и вторым и третьим.
2.30 яиц, так как 30 – наименьшее общее кратное чисел 6 и 10.
3 препятствие.
Математика – точильный камень способностей.
1.Найдите наибольший общий делитель чисел :
1).42 и 60; 2).45 и 81; 3).72 и 63; 4).120 и 96.
2.Найдите наименьшее общее кратное чисел:
1).45 и 54; 2)32 и 48; 3)90 и 75; 4)72 и 96.
3.Прочитайте вслух и скажите верно, или не верно утверждение.
Если число а делится на число в, значит, а кратно в.
Если число а делится на число в, значит, в - делитель а.
8 кратно 32.
Число 36 является наименьшим общим кратным чисел 12 и 36.
Числа 22, 44, 66, 88 кратны 11.
НОД(8;16;32) = 32.
НОК(8;16;32) = 32.
Число 18 кратно 6, значит НОД(18;6) = 18.
Если два числа взаимно простые, то их наименьшее общее кратное равно произведению данных чисел.
4 препятствие.
Математика черпает свою силу в умении исключать все лишнее в процессе мышления.
(Э.Мах)
1.Один из трех поездов, которые вышли со станции Алматы, возвращается назад через 3 дня, второй поезд- через 6 дней, третий поезд- через 5 дней. Через сколько дней эти поезда встретятся на станции Алматы?
2.Алла и Маша идут рядом. Длина одного шага Аллы 40 см, а Маши -60 см. Какое расстояние пройдут девочки, когда их шаги совпадут?
3.Для приготовления новогодних детских подарков купили 200 апельсинов,240 шоколадок и 320 орехов. Какое количество подарков можно сделать, разделив каждое число апельсинов, шоколадок и орехов поровну?
4.Закончи фразу:
Если число делится на 3, то.
Если сумма цифр числа делится на 9, то.
Если число делится на 3, то на 9 оно.
Натуральное число не делится на 2, если.
На 10 делятся числа,.
Натуральное число делится на 2, 5 и 10, если.
Число 24 681 на 3., так как сумма его цифр равна. и на 3
Число. кратно любому натуральному числу
9. Делителем любого натурального числа является.
(Дермохелис)
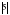- Р;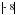 
- И; 6,1 – Ф; 16 –П; -0,2 –Г; 0,2 –А; -0,6 – О.
