| Планируемые сроки | Время | Планируемые действия | Ресурсы |
| Начало урока: | |
|
|
| 1.Организационный этап
| 1 мин
| Подготовка к уроку. Приветствие. Кратко сообщить план урока. Формирование групп по номерам 1, 2, 3,4. Распределение ролей в группах. |
|
| 2. Фаза вызова а) | 1мин
4 мин | Озвучивание цели урока, принятие ее учащимися, мотивация их дальнейшей деятельности. Прием «Я уже знаю» (кластер). Ваши ассоциации по теме «Комбинаторика», учитель предлагает учащимся за определенное время выписать как можно больше слов или выражений ,связанных по их мнению ,с комбинаторикой . 1 этап. Учащиеся выполняют работу индивидуально. 2 этап. Обсуждение полученных записей в парах или группах. Учащиеся выделяют подобные представления, наиболее оригинальные идеи, вырабатывают коллективный вариант ответа. 3 этап- «Сброс идей в корзину». Каждая пара или группа поочередно называет одно из выражений. Учитель фиксирует их на доске. Предложения не должны повторяться. В результате на доске формируется кластер, в котором отражаются знания учащихся по данной теме, что позволит учителю диагностировать уровень подготовки классного коллектива и использовать данную схему, как опорную, при объяснении нового материала.
|
|
|
| 4 мин | Прием «Ключевые слова»: знаю-хочу узнать- узнал. Рассказ правила по ключевым словам. |
|
| Середина урока | | Мозговой штурм Задача 1. В некотором учреждении имеются две различные вакантные должности, на каждую из которых претендуют три сотрудника: A, B, C. Сколькими способами из этих трех кандидатов можно выбрать два лица на эти должности? Задача 2. Для участия в соревнованиях требуется выбрать двоих спортсменов из трех кандидатов: A, B, C. Сколькими способами можно осуществить этот выбор? Ученикам предлагается два проблемных задания: 1) установить различие между этими двумя внешне схожими задачами и 2) предположить, в какой задаче результат будет больше, и почему. После этого предлагается решить эти задачи методом перебора всевозможных вариантов. Решение задачи 1. AB, BA, BC, CB, AC, CA (всего шесть способов). Решение задачи 2. AB, BC, AC (всего три способа). Учитель обращает внимание учеников на то, что эти задачи оказались похожими только внешне, из - за того, что в обеих присутствуют два числа: n=3 – общее количество элементов и m=2 – количество выбранных элементов. Но в первой задаче составляются упорядоченные соединения, тогда как во второй задаче порядок следования элементов в соединении не имеет значения.
|
|
| 3. Фаза реализации смысла | 10 мин | «Пометки на полях» (инсерт). Предлагаю проработать образцы заданий к новому параграфу, используя установленную знаковую систему. Учащиеся внимательно знакомятся с решением задания, делая карандашом соответствующие пометки в тексте: «V» -.то, что было известно учащимся ранее; «+»- новая информация; «-» - информация, противоречащая взглядам учащихся; «?» - информация не вполне понятна. Полученные новые сведения можно оформить в виде таблицы Вы можете поставить одну или две пометки на абзац, иногда больше или меньше. Теперь приступайте к чтению статьи, не забывая ставить пометки. Когда все группы закончат чтение и обсуждение текста, им нужно выбрать для объяснения данного текста всему классу страницы из презентаций, дополняющие их объяснение и построить логическое представление темы текста. Учитель раздает тексты с новым материалом, и учащиеся работают в группах над этим текстом. Для активного обсуждения проблемы на уроке следует: - поощрять обмен мнениями между участниками группы; - попросить участников вносить ясность в ответы и отстаивать их; - проводить время от времени обзор аргументов; - следить за вопросами участников, чтобы не пропустить поднятый кем-то удачный вопрос; |
|
|
|
| Группа 1 Из глубокой древности до современного человечества дошли сведения о том, что уже тогда люди занимались выбором объектов и расположения их в том или ином порядке и увлекались составлением различных комбинаций. Так, например, в Древнем Китае увлекались составлением квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же (современная игра – задача “Судоку”). Такие задачи вы могли встречать в журналах и газетах. В Древней Греции подобные задачи возникали в связи c такими играми, как шашки, шахматы, домино, карты и т.д. Комбинаторика ставится самостоятельным разделом математики, по сути – самостоятельной наукой лишь во второй половине XVII века, - в период, когда возникла теория вероятностей. Таким образом, - комбинаторика – это самостоятельный раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или условиям, можно составить из заданных объектов. Комбинаторика – самостоятельная ветвь математической науки. Термин “КОМБИНАТОРИКА” происходит от латинского слова “combina”, что в переводе на русский означает – “сочетать”, “соединять” - Как трактует это слово Большой Энциклопедический Словарь? Комбинаторика – это раздел математики, в котором изучаются простейшие “соединения”: перестановки, размещения, сочетания. Этот раздел иначе называют “комбинаторный анализ”. Сегодня мы будем рассматривать перестановки, размещения, сочетания, как соединения, как комбинаторные конфигурации. Разделы комбинаторики: перечислительная, структурная, вероятностная, топологическая Давайте вспомним известное вам из детства сказание о том, как богатырь или другой добрый молодец, доехав до развилки трех дорог, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый КОМБИНАТОРИКОЙ, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую – Итак, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений. |
|
|
| | Группа 2 Перестановки-соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их 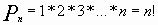 Количество всех перестановок из n элементов обозначают Количество всех перестановок из n элементов обозначают 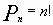
Число n при этом называется порядком перестановки Произведение всех натуральных чисел от n до единицы, обозначают символом n! (Читается “эн - факториал”). Используя знак факториала, можно, например, записать: 1! = 1, 2! = 2•1 = 2, 3! = 3 •2 •1 = 6, 4! = 4 •3 •2 •1 = 24, 5! = 5 •4 •3 •2 •1 = 120. Необходимо знать, что 0!=1 Термин “перестановки” употребил впервые Якоб Бернулли в книге “Искусство предположений”. Примеры решения задач: Задача №1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд? Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п. Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг. Ответ: 5040 способов. Задача № 2 (о квартете) В знаменитой басне Крылова “Квартет” “Проказница мартышка, Осел, Козел да косолапый Мишка” исследовали влияние взаимного расположения музыкантов на качество исполнения. Зададим вопрос: Сколько существует способов, чтобы рассадить четырех музыкантов? Задания для решения задач в группе: Сколькими способами Дима и Вова могут занять 2 места за одной двухместной партой? Из трёх стаканов сока – яблочного, сливового и абрикосового – Коля решил последовательно выпить два. Перечислите все варианты, которыми это можно сделать. Сергей, Игорь и Миша могут занять 1-е, 2-е и 3-е призовые места в соревнованиях по шахматам. Перечислить всевозможные последовательности из имён мальчиков, где порядковый номер в последовательности соответствует занятому мальчиком месту в У Влада на обед – первое, второе, третье и пирожное. Он обязательно начнёт с пирожного, а всё остальное съест в произвольном порядке. Найдите число возможных вариантов обеда. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре? Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге. Семь мальчиков, в число которых входят Сергей и Игорь, становятся в ряд. Найдите число возможных комбинаций, если: а) Сергей должен находиться в конце ряда; б) Сергей должен находиться в начале ряда, а Игорь – в конце ряда; в) Сергей и Игорь должны стоять рядом. Одиннадцать футболистов школьной команды строятся перед началом матча. Первым становится капитан, вторым – вратарь, а остальные – случайным образом. Сколько существует способов построения? В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, химия, физкультура. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
|
|
| | | Группа 3 Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их. 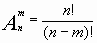
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны. В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания). Термин “Размещение” употребил впервые Якоб Бернулли в книге “Искусство предположений”. Примеры решения задач: Задача № 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений. Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет: 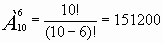 Ответ:151200 способов Задача № 2. В классе обучается 24 ученика. Сколькими способами можно составить график дежурства по классу, если группа дежурных состоит из трех учащихся? Решение: число способов равно числу размещений из 24 элементов по 3, т.е. равно А243. По формуле находим 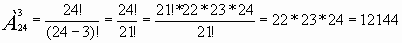
Ответ: 12144 способа Задания для решения задач в группе: Размещения 1. Из трёх стаканов сока – ананасового, брусничного и виноградного – Костя решил последовательно выпить два. Сколькими способами это можно сделать? 2. Сколькими способами могут быть заняты первое, второе и третье места (по одной команде на место) на соревнованиях по гимнастике, в которых участвуют 6 команд? 3. Из 26 учащихся класса надо выбрать старосту и его заместителя. Сколькими способами это можно сделать? 4. На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4100 м на первом, втором, третьем и четвёртом этапах? 5. Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса? 6. Сколькими способами 6 девятиклассников, сдающих экзамен, могут занять места в кабинете, в котором стоит 15 столов? 7. Сколько команд участвовало в финале первенства города по хоккею, если каждая команда сыграла с каждой из остальных по одной игре на своём поле и по одной игре на поле соперника, причём всего было сыграно 30 игр? 8. В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории, литературе, русскому и английскому языкам? 9. Учащиеся 9 класса изучают 14 предметов. Сколькими способами можно составить расписание уроков на один день так, чтобы было 6 различных уроков? |
|
|
| | Группа 4 Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их 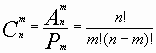 . . Таким образом, количество вариантов при сочетании будет меньше количества размещений В комбинаторике сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Термин “сочетание” впервые встречается у Блеза Паскаля в 1665 году. Примеры решения задач: Задача №1. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр? Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок – сочетание. Отсюда возможно 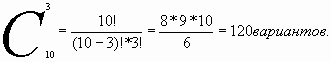
Ответ: 120 вариантов. Задача № 2. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей? Решение: По формуле находим: 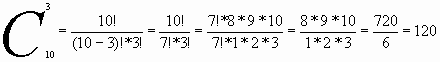 комиссий комиссий
Ответ: 120 комиссий. Задания для решения задач в группе: Сочетания 1. Имеется три предмета: карандаш, тетрадь и линейка. Сколькими способами из этих канцелярских принадлежностей можно выбрать 2 предмета? способа. 2. В школьной столовой имеются помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? Записать все сочетания овощей в составленных салатах. 3. Володя идёт на день может сделать подарки братьям? 4. В магазине продают кепки трёх цветов: белые, красные и синие. Наташа и Лена покупают себе по одной кепке. Сколько существует различных вариантов покупок для этих девочек? 5. Сколько существует способов выбрать троих ребят из 11 желающих дежурить по школе? 6. В 9 «Г» классе 5 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде? 7. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг? 8. В 9 «Г» классе учатся 16 мальчиков и 10 девочек. Для уборки территории требуется выделить четырёх мальчиков и трёх девочек. Сколькими способами можно это сделать? 9. В библиотеке Кате предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами она может выбрать из них 3 книги и 2 журнала? 10. В 9 «Б» классе учатся 22 учащихся, в 9 «В» - 19 учащихся, а в 9 «Г» - 26 учащихся. Для работы на пришкольном участке надо выделить трёх учащихся из 9 «Б» класса, двух – из 9 «В» и одного – из 9 «Г». Сколько существует способов выбора учащихся для работы на пришкольном участке? 11. По списку в 9 «Г» классе 16 мальчиков и 10 девочек. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать: а) при условии. Что пару обязательно должны составить мальчик и девочка; б) без указанного условия? 12. По списку в 9 «Г» классе 16 мальчиков и 10 девочек. Нужно выбрать двух дежурных по классу. Нужно выделить группу из трёх человек для посещения заболевшего одноклассника. Сколькими способами это можно сделать, если: а) все члены этой группы должны быть девочками; б) все члены этой группы должны быть мальчиками; в) в группе должны быть 1 девочка и 2 мальчика; г) в группе должны быть 2 девочки и 1 мальчик. |
|
|
| 15 мин | Презентация. Защита данной темы и рассмотрение примеров каждой группы |
|
| Конец урока | 1 мин | Термины «перестановки» и «размещения» впервые употребил Якоб Бернулли в книге «Искусство предположений».
Термин «сочетания»впервые встречается у Блеза Паскаля в 1665 году. Общее у всех этих задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. “Особая примета” комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался словами: “Сколькими спосособами…?”. |
|
| Дифференциация: Как вы планируете поддерживать учащихся?
|
| Оценивание кластера: Качественное содержание Наличие всех ключевых понятий Наличие слов привязок (по 5 бальной системе) Оценивание защиты кластера: Доступность Наглядность Краткость Жизненно-важные навыки | Межпредметные связи: СанПиН ИКТ компетентность Связи с ценностями |
| Фаза рефлексии:
| 3 мин | «Написание синквейна». «синквейн» -это стихотворение, представляющее собой синтез информации в лаконичной форме, что позволяет описывать суть понятия или осуществлять рефлексию на основе полученных знаний”. Слово происходит от французского “5”. Это стихотворение из 5 строк, которое строится по правилам:
1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза из четырех слов, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово). Синквейн дает возможность подвести итог полученной информации, изложить сложные идеи, чувства и представления в нескольких словах. Синквейн может выступать в качестве средства творческого самовыражения. Спасибо за урок!
|
|
| Итог урока, домашнее задание | 2 мин | 1.“Ромашка” Блума. По теме составить вопросы, учитывая их назначение.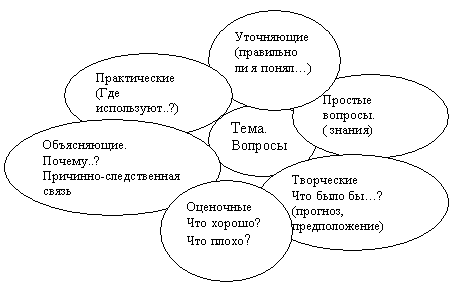 |
|
Оценочный лист. Фамилия, Имя
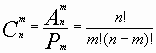 .
.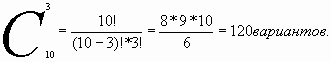
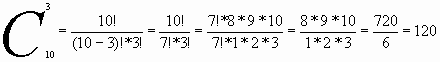 комиссий
комиссий
















