Определенный интеграл и его непосредственное интегрирование

Занятие № 26. Определенный интеграл и его непосредственной вычисление.

Цель – обобщить, систематизировать и дополнить знания обучающихся по теме «Определенный интеграл».

Задачи: 1. Обобщить теоретический материал по теме «Определенный интеграл»; 2. Формировать у обучающихся навыки вычисления определенных интегралов; 3. Развивать математическую культуру, логическое мышление, внимание; 4. Воспитывать дисциплинированность, аккуратность, усидчивость.

Ход занятия.

I. Организационный момент.

II. Опрос.

III. Теоретическая часть.

1. Определенный интеграл и его непосредственное вычисление.

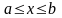Пусть функция f(x) определена на отрезке . Разобьем этот отрезок на n частей точками 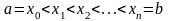, выберем на каждом элементарном отрезке 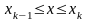произвольную точку 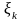и обозначим через 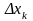длину каждого такого отрезка. Интегральной суммой для функции 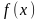на отрезке называется сумма вида .

Опр.1. Определенным интегралом от функции на отрезке называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

.

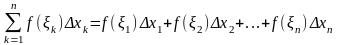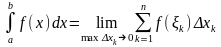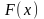Для вычисления неопределенного интеграла от функции в том случае, когда можно найти соответствующий неопределенный интеграл , служит формула Ньютона-Лейбница:

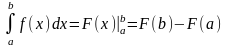, т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.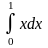

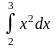
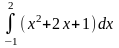
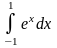
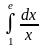
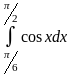
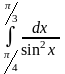
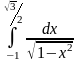
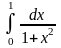
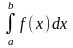Пример. Вычислить определенные интегралы:

1.

2.

3.

4.

5.

6.

7.

8.

9.

2. Вычисление определенного интеграла методом замены переменной.

При вычислении определенного интеграла методом замены переменной определенный интеграл преобразуется с помощью подстановк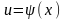и или 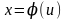в определенный интеграл относительно новой переменной u. При этом старые пределы интегрирования a и b заменяются новыми пределами интегрирования 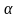и 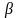, которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: , .

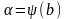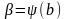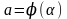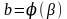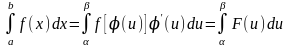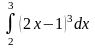
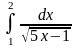
Из второй подстановки новые пределы интегрирования находятся путем решения уравнений и относительно 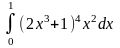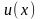и .

Таким образом, имеем .

Пример. Вычислить определенные интегралы:

1)

2)

3) .

3. Интегрирование по частям в определенном интеграле.

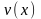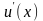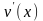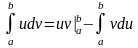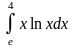_{Если функции} и и их производные и непрерывны в промежутке _{, то формула интегрирования по частям для определенного интеграла имеет вид: .}

_{Пример. Вычислить .}