Конспект
обобщающего урока по теме «Векторы на плоскости»
(геометрия 9 класс)
Тема. Систематизация и обобщение изученного материала по теме
«Векторы на плоскости».
Цели:
проверить знания основных понятий и формул по векторам;
формировать навыки в умении решать ключевые задачи по данной теме, применяя известные понятия, свойства и формулы по векторам;
способствовать развитию умения ориентироваться в теоретическом материале, выделять главное, необходимое для решения задач;
формировать навыки самообразовательной деятельности;
воспитание культуры устной и письменной математической речи;
умения общаться, толерантности отношений, интереса к предмету.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: презентация, рекламы, организационные листы, учебник.
ХОД УРОКА
Организационный момент.
Мотивация учебной деятельности.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело: чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать совету этого писателя. Будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.
Постановка целей и задач.
Сегодня у нас заключительный урок по теме «Векторы». Сначала давайте определимся с целями и задачами нашего урока. Что мы должны закрепить, чему научиться, что развивать в себе?
(Учащиеся отвечают)
Итак, цели и задачи поставлены, приступим к работе по их выполнению.
Проверка домашнего задания.
Переходим к проверке домашнего задания. Оно было творческого характера: Подготовить рекламу по теме «Векторы на плоскости».
( Афиширование реклам. Выступление учащихся с рекламой.)
Проверка глубины осмысления учащимися знаний по изученной теме.
Просмотрев рекламы, мы немного вспомнили о векторах.
А теперь, мы с вами отправимся в увлекательное путешествие, во время которого более подробного остановимся на этой теме. Но будьте очень внимательны. Это путешествие необычное.
Вы получили организационные листы с заданиями.
«Понятийное поле». В графе «Понятия» вы должны вписать те понятия, о которых вам поможет вспомнить пшеничное поле.
Представьте, что вы стоите перед полем, засеянном пшеницей. Полюбуйтесь его красотой. Рассмотрите налитые силой колосья, почувствуйте запахи этого поля. Вдохните аромат нивы. Прислушайтесь к звукам, которые вас окружают: шелесту пшеницы, пению птиц. Ощутите легкий ветерок на своем лице. Пройдитесь по этому полю. Попросите его стать символом понятия «Вектор».
А теперь представьте, что ветер стих. Наклонитесь и рассмотрите один стебелек. Из маленького зернышка, закопанного в землю, он вырос, стремясь, к солнцу, один выше, один ниже, но посмотрите, какими они стали сильными, мощными. Стебель сам как вектор: зернышко, брошенное в землю, это его начало, а прекрасное соцветие-колос – конец. Его направление – это движение к солнцу. Но не все зернышки проросли. Некоторые из них остались лежать в земле, став и началом и концом.
Посмотрите на поле, все стебли параллельны. Все колосья как стрелы направлены вверх. Среди них есть разной длины, а есть и равные по длине.
Сорвите колос и опустите его вертикально вниз соцветием. Он направлен в противоположную сторону с любым растущим колосом. Поблагодарите поле пшеницы за то, что оно помогло нам вспомнить понятие о векторе.
А сейчас обсудим, что кому удалось рассмотреть.
(Дети зачитывают понятия, которые им удалось «увидеть»)
Понятийное поле. Понятие вектора, изображение и обозначение, нулевой вектор, коллинеарные векторы, одинаково направленные, равные, противоположно направленные, противоположные векторы, характеристические данные: длина и направление.
За каждые правильные 3 ответа ставим 1 балл
Продолжаем путешествие по полю.
Посмотрите на рисунок. Отметьте точку на поле, где вы стоите с другом. Солнышко припекает, хочется спрятаться в тенек. Вы увидели дерево и куст, растущие в поле. Ваш друг пошел спрятаться в тени куста, а вы в тени дерева. Изобразите на рисунке направленным отрезком (ā) свой путь к дереву, а путь друга – вектором (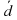 ). Друг в тенёчке уснул, а вы вдруг увидели родник, и быстро направились к нему, чтобы испить воды. Покажите на рисунке свое перемещение (
). Друг в тенёчке уснул, а вы вдруг увидели родник, и быстро направились к нему, чтобы испить воды. Покажите на рисунке свое перемещение (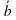 ). А теперь покажите, как бы вы прошли к ручью, если бы вы его увидели сразу (
). А теперь покажите, как бы вы прошли к ручью, если бы вы его увидели сразу (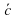 ). Посмотрите внимательно на рисунок и запишите как можно вектор (
). Посмотрите внимательно на рисунок и запишите как можно вектор (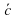 ) выразить через векторы (ā) и (
) выразить через векторы (ā) и (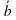 ) (сумма векторов по правилу треугольника и разность векторов). Друг проснулся и только увидев родник, направился к нему. Покажите его движение вектором (
) (сумма векторов по правилу треугольника и разность векторов). Друг проснулся и только увидев родник, направился к нему. Покажите его движение вектором (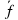 ). Что является суммой векторов (
). Что является суммой векторов (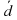 ) и (
) и (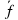 ). Суммой каких векторов еще является вектор (
). Суммой каких векторов еще является вектор (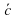 )?
)?
Какое еще действие мы можем выполнять с векторами? (умножение вектора на число).
На рисунке отложите вектор (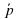 ) = 2ā и (
) = 2ā и (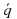 ) = -1,5
) = -1,5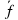
Подвести итоги этого задания.
Какой способ выполнения действий с векторами мы использовали? Какой способ можно еще применить? (аналитический) Для этого нам необходимо вспомнить формулы.
В организационном листе задание №3 изображена таблица, в которой вы должны определить соответствие между понятиями и формулами.
Координаты вектора | А) х1х2 + у1у2 |
Длина вектора | Б) (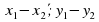 ) ) |
Сумма векторов | В) (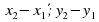 ) ) |
Разность векторов | Г) 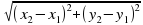 |
Умножение вектора на число | Д) (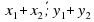 ) ) |
Условие коллинеарности | Е) х1х2 + у1у2 = 0 |
Условие перпендикулярности | Ж) 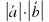 cos( cos(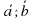 ) ) |
Скалярное произведение векторов. | З) ( 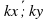 ) ) |
|
| И) 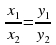 |
Проверим правильность ваших ответов:
1 - В; 2 - Г ; 3 - Д ; 4 - Б ; 5 - З ; 6 - И ; 7 - Е ; 8 - А, Ж .
За каждый правильный ответ вы ставите 0,5 баллов
Вопрос классу (отвечают учащиеся).
Чем отличается результат действий сложения, вычитания, умножения вектора на число от результата скалярно произведения?
Как определить вид треугольника с помощью векторов?
Как доказать, что данный четырехугольник параллелограмм?
Как доказать, что параллелограмм – является ромбом?
Как найти неизвестные координаты вершины параллелограмма?
Как определить вид треугольника по углам и сторонам?
Мы с вами вспомнили основные понятия и формулы и теперь приступим к решению задач. Сейчас небольшая разминка. Решаем тестовые задания. Задание №4 организационного листа.
Тестовые задания.
Найти координаты вектора 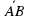 , если А(3;-4), В(0;2).
, если А(3;-4), В(0;2).
А) (3;-2); Б) (3;-6); В) (-3;6); Г) (-3;-2).
Вычислить модуль вектора 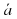 (-1;4).
(-1;4).
А) 3; Б) 5; В) 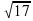 ; Г)
; Г) 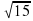 .
.
При каком значении х векторы 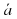 (4;2) и
(4;2) и 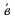 (х;-4) коллинеарны?
(х;-4) коллинеарны?
А) -2; Б) 2; В) -8; Г) 8.
Вычислить скалярное произведение векторов 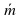 (5;-4) и
(5;-4) и 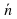 (2;3)
(2;3)
А) -4; Б) 4; В) 2; Г) -2.
При каком значении n векторы 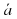 (n;3) и
(n;3) и 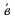 (-3;3) перпендикулярны?
(-3;3) перпендикулярны?
А) -3; Б) 3; В) -2; Г) 2.
Определить вид угла между векторами 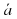 (-3;5) и
(-3;5) и 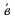 (-4;-2).
(-4;-2).
А) тупой; Б) острый; В) прямой; Г) определить невозможно.
Выполняем взаимопроверку. 1-В; 2-В; 3-В; 4-Г; 5-Б; 6-Б.
За каждый правильный ответ ставим 0,5 баллов.
А теперь решим следующие задачи
1-вариант. Доказать, что четырехугольник АВСD с вершинами в точках А(-1;5), В(4;6), С(3;1), D(-2;0) является ромбом.
2-вариант. Найти косинусы углов треугольника АВС, если А(1;-4), В(4;7), С(-2;1). Установить вид треугольника.
Решение выполняют 2 человека у доски, остальные в тетрадях по вариантам. Комментирование решения.
Оценивание.
Домашнее задание.
Повторить §12 - §17.
Решить по сборнику
6 баллов: задание №12 из 1 части варианты: 7, 14, 21, 25, 33, 39.
9 баллов: задания со 2 части вариант 5, 10 задание №5, вариант 12,15 задание №6.
12 баллов: по учебнику №606, 609.
По желанию подготовить кроссворд по изученной теме.
Итог урока.
Наш урок подошел к концу. Давайте подведем итог урока. У вас в организационных листах записаны 4 предложения:
Я все знаю, понял и могу объяснить другому.
Я всё знаю, понял, но не уверен, что смогу объяснить другому.
Я сам знаю, понял, но не смогу объяснить другому.
У меня остались некоторые вопросы.
Проанализируйте предложения и выберите вариант соответствующий вашим ощущениям.
Подымите руки, кто выбрал 1 предложение? 2 - ? 3 - ? 4 - ? Из ваших ответов можно сделать вывод, что материал по этой теме в основном усвоен, но есть еще вопросы над которыми надо поработать. Поэтому, как сказал великий мудрец «Всё в ваших руках». Ваши успехи, достижения – зависят только от вашего старания, настойчивости в достижении цели. Консультацию и помощь вы всегда можете получить.
На этом урок закончен. Спасибо за сотрудничество.
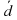 ). Друг в тенёчке уснул, а вы вдруг увидели родник, и быстро направились к нему, чтобы испить воды. Покажите на рисунке свое перемещение (
). Друг в тенёчке уснул, а вы вдруг увидели родник, и быстро направились к нему, чтобы испить воды. Покажите на рисунке свое перемещение (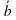 ). А теперь покажите, как бы вы прошли к ручью, если бы вы его увидели сразу (
). А теперь покажите, как бы вы прошли к ручью, если бы вы его увидели сразу (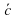 ). Посмотрите внимательно на рисунок и запишите как можно вектор (
). Посмотрите внимательно на рисунок и запишите как можно вектор (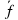 ). Что является суммой векторов (
). Что является суммой векторов (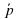 ) = 2ā и (
) = 2ā и (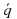 ) = -1,5
) = -1,5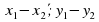 )
)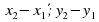 )
)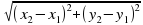
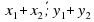 )
)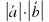
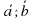 )
)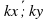
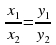
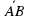 , если А(3;-4), В(0;2).
, если А(3;-4), В(0;2).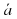 (-1;4).
(-1;4).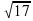 ; Г)
; Г) 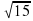 .
. 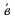 (х;-4) коллинеарны?
(х;-4) коллинеарны?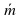 (5;-4) и
(5;-4) и 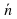 (2;3)
(2;3)



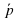 = 2ā и
= 2ā и 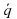 = -1,5
= -1,5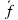
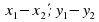 )
)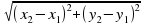
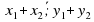 )
)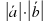
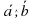 )
)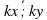
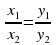
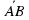 , если А(3;-4), В(0;2).
, если А(3;-4), В(0;2).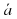 (-1;4).
(-1;4).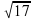 ; Г)
; Г) 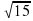 .
. 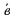 (х;-4) коллинеарны?
(х;-4) коллинеарны?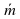 (5;-4) и
(5;-4) и 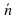 (2;3)
(2;3)






























