Цели урока
Образовательные:
- Повторение теоретического материала: определение логарифма и его свойства, свойства логарифмической функции, способы решения логарифмических уравнений и неравенств;
- Формирование и закрепление навыков решения логарифмических уравнений и неравенств;
- Показать необходимость глубоких знаний по данной теме при подготовке к ЕНТ.
Воспитательная: воспитывать сознательное отношение к учебе, повышение интереса к математике
Развивающая: развивать логическое мышление, математическую речь, умение сравнивать и делать выводы; совершенствовать навыки работы со свойствами логарифмов и применять их при решении уравнений и неравенств.
Задачи урока
- Научить оперировать имеющимся потенциалом знаний в конкретной ситуации;
- Закрепление основных методов решения логарифмических уравнений и неравенств, предупреждение появления типичных ошибок;
- Рассмотреть задания из сборников ЕНТ для подготовки к экзамену;
- Содействовать воспитанию положительного отношения у учебе, настойчивости в достижении целей, интереса к математике.
Формы урока: фронтальная, групповая, дифференцированная, индивидуальная.
Методы и приемы: наглядно-иллюстративный, репродуктивный, частично-поисковый, практический.
Оборудование: проектор, карточки для самостоятельной и групповой работы.
Ход урока
I. Организационный момент.
Цели и задачи урока: обобщить и систематизировать знания при решении логарифмических уравнений и неравенств, проверить прочность усвоения знаний, подготовиться к контрольной работе и к ЕНТ.
II. Актуализация знаний.
- Фронтальная работа (теоретическая) Проверка методом приёма « Да-нет»
Вопросы – задания, на которые ученики отвечает «да» или «нет»
1. Логарифмическая функция y=log аx определена при любом х.(-)
2. Функция y=logax логарифмическая при a>0, a=0, x>0.(+)
3. Область определения логарифмической функции является множество действительных чисел.(-)
4. Область значений логарифмической функции является множество действительных чисел.(+)
5. Логарифмическая функция – четная.(-)
6. Логарифмическая функция – нечетная.(-)
7. Функция y=log 3 x – возрастающая.(+)
8. Функция y=log 0,3 x – возрастающая.(-)
9. Логарифмическая функция имеет экстремум в точке (1;0).(-)
10. График функции y=logax пересекается с осью Ох.(+)
11. График логарифмической функции находится в верхней полуплоскости.(-)
12. График логарифмической функции симметричен относительно Ох.(-)
13. График логарифмической функции всегда находится в I и IV четвертях.(+)
14. График логарифмической функции всегда пересекает Ох в точке (1;0).(+)
15. Существует логарифм отрицательного числа.(-)
16. Существует логарифм дробного положительного числа.(+)
17. График логарифмической функции проходит через точку (0;0).(-)
Да(+); Нет(-)
Ответы вывешиваются на доске.
- + - + - + - + - + + - + -
Работа в парах по проверке результатов.
- Устный счет( кодоскоп)
Найти число х:
log3x = -1 ответ х=1\3
log4x = -3 ответ х=1\64
log1\2x= 0 ответ х=1
Вычислить:
log2 16= ответ 4
log0,2 0,04= ответ 2
log23 1= ответ 0
- Алгоритм решения уравнений и неравенств (коллективное повторение алгоритмов решения)

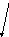


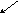
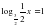 б) log4 (9x2 +
б) log4 (9x2 +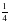 ) =
) =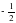 в) lg (3 – 4x) – lg (- 5x – 2) = 0
в) lg (3 – 4x) – lg (- 5x – 2) = 0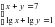
 x – 3 log3x -2 = 0
x – 3 log3x -2 = 0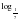 (2x + 3) 7 (3x -2) б) log22x – log2x 6
(2x + 3) 7 (3x -2) б) log22x – log2x 6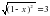 .
. x=2.
x=2. 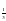 x≥-2 .
x≥-2 .  (13-x) = 2.
(13-x) = 2.  (x+3 )= log
(x+3 )= log 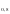 (x
(x -4x-20) ≤ 0.
-4x-20) ≤ 0.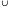 [7;+ ∞). Д) [-3;2-2
[7;+ ∞). Д) [-3;2-2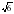 )
)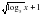 .
.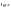 =5х-11.
=5х-11.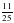 Д) -2,2. Е) 10
Д) -2,2. Е) 10















