Саба?ты? та?ырыбы: §10. Негізгі тригонометриялы? те?бе – те?діктер
Саба?ты? ма?саты:
Білімділік: Негізгі тригонометриялы? те?бе – те?діктерді ?рнектейтін формулаларды білу, ?рнектерді ы?шамдауда, те?бе – те?діктерді д?лелдеуде ?олдана білу.
Дамытушылы?: О?ушыларды? ?з бетінше ой ?орыта білу ж?не математика тілінде с?йлеу да?дыларын ?алыптастыру.
Т?рбиелік: О?ушыларды ?зара бір-біріне к?мек беруге ?йрету ж?не адамгершілікке т?рбиелеу.
.
Саба? т?рі: Жа?а білімді игеру
К?рнекілігі: интерактивті та?та, слайд, дидактикалы? материалдар
Саба?ты? барысы: 1. ?йымдастыру кезе?і
- Жа?а саба?ты баяндау
Просмотр содержимого документа
«Негізгі тригонометриялы? те?бе-те?діктер»
Сабақтың тақырыбы: §10. Негізгі тригонометриялық теңбе – теңдіктер
Сабақтың мақсаты:
Білімділік: Негізгі тригонометриялық теңбе – теңдіктерді өрнектейтін формулаларды білу, өрнектерді ықшамдауда, теңбе – теңдіктерді дәлелдеуде қолдана білу.
Дамытушылық: Оқушылардың өз бетінше ой қорыта білу және математика тілінде сөйлеу дағдыларын қалыптастыру.
Тәрбиелік: Оқушыларды өзара бір-біріне көмек беруге үйрету және адамгершілікке тәрбиелеу.
.
Сабақ түрі: Жаңа білімді игеру
Көрнекілігі: интерактивті тақта, слайд, дидактикалық материалдар
Сабақтың барысы: 1. Ұйымдастыру кезеңі
Жаңа сабақты баяндау
§10. Негізгі тригонометриялық теңбе-теңдіктер
α сүйір бұрышының әрбір мәніне сәйкес sinα-ның, cosα-ның, tgα-ның және ctgα-ның мәндерін анықтауға болады.
1. Катеттері а мен b, гипотенузасы с болатын, ал сүйір бұрыштары α мен β-ға тең АВС тік бұрышты үшбұрышы берілсін. Пифагор теоремасын жазамыз:
a2+b2=c2 (*)
§8, (1) және (2) формулалардан b=ccosα, a=csinα болатыны белгілі. Осы мәндерді (*) –ға қойсақ,
sin2α+cos2α=1 (1)
шығады. Бұл α бұрышының синусы мен косинусын байланыстыратын теңбе-теңдік.
2. Берілген тікбұрышты үшбұрыш үшін
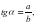 ctgα=
ctgα=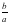
болатыны белгілі. Бұл теңдіктерге b=ccosα, a=csinα мәндерін қойсақ,
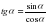 (2)
(2)
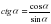 (3)
(3)
Аламыз. Бұл теңдіктер кез-келген α сүйір бұрышы үшін орындалатын теңбе-теңдік болып саналады.
3. (1) тепе-теңдік әрбір мүшесін сos2α-ға немесе sin2α-ға бөліп, төмендегідей екі тепе-теңдікті алуға болады:
1+tg2α=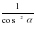 (4)
(4)
1+ctg2α=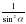 (5)
(5)
4. АВС тікбұрышты үшбұрышына сүйір бұрыштар үшін α+β=900 өрнегі Бұдан β=900-α. 30-суреттен sin=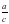 , ал cosβ=
, ал cosβ=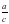 сондықтан cos(900-α). Сонда
сондықтан cos(900-α). Сонда
cos(900-α) =sinα (6)
теңбе-теңдігін аламыз. Осы сияқты
sin(900-α)=cosα (7)
теңбе-теңдігін алуға болады.
3. Есептер шығару
Оқулықпен жұмыс
№144. Өрнекті ықшамдаңдар
2+sin2α+cos2α=2+1=3
(1 – sinα )(1+sinα)=1-sin2α=cos2α
№145.
(1+ctg2α)∙sin2α+1=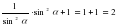
tgα∙ctgα+sinα=1+sinα
4. Үйге тапсырма: §10 №144 (2), 145 (2)
5. Қорытындылау
Слайд 1.sin2α+cos2α=1
2. 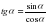 5. 1+ctg2α=
5. 1+ctg2α=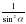
3. 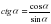 6. cos(900-α) =sinα
6. cos(900-α) =sinα
4. 1+tg2α=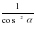 7. sin(900-α)=cosα
7. sin(900-α)=cosα
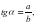 ctgα=
ctgα=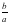
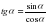 (2)
(2)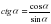 (3)
(3)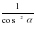 (4)
(4)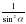 (5)
(5)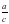 , ал cosβ=
, ал cosβ=