N[YJKJUBZ РАБОТЫ С ГЕОМЕТРИЧЕСКОЙ ЗАДАЧЕЙ

Глава «Соотношения между сторонами и углами треугольника», дополнительные задачи.

Подробно рассмотрено решение задачи с разбором основных направлений рассуждения и доказательства.

Урок рассчитан на учащихся различного уровня подготовлнности.

методическая разработк будет полезна учителям начинающим свою деятельность, а так же студентам педагогических ВУЗов

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«n[YJKJUBZ РАБОТЫ С ГЕОМЕТРИЧЕСКОЙ ЗАДАЧЕЙ»

Технология работы с геометрической задачей

Класс 7, Глава «Соотношения между сторонами и углами треугольника», дополнительные задачи

Задача 305. Докажите, что сумма расстояний от любой точки, лежащей внутри треугольника, до его вершин меньше периметра треугольника.

Дано:

Δ АВС,

Точка М лежит внутри Δ АВС,

Доказать:

Р_АВСМВ+МА+МС

Вопросы учителя	Ответы учащихся	Записи в тетради и на доске
Прочитайте условие задачи. Что дано, что необходимо доказать?	Даны произвольный треугольник и принадлежащая ему точка.
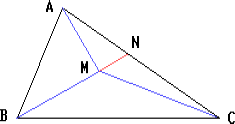
Постройте чертеж для задачи.		Дано: Δ АВС, М Δ АВС, Доказать: Р_АВСМВ+МА+МС
Что вы можете определить по рисунку?	Треугольник АВС разбит на три треугольника: Δ АВМ, Δ МВС, Δ АМС.	ΔАВМΔ АВС ΔМВСΔ АВС ΔАМСΔ АВС
Какой вывод из этого следует?	Что стороны этих треугольников меньше соответствующих сторон большего треугольника	ΔАВМΔ АВС ΔМВСΔ АВС ΔАМСΔ АВС
Охарактеризуйте треугольники АВС и АВМ	Треугольник АВМ лежит внутри треугольника АВС. Длины двух сторон внутреннего треугольника всегда меньше Периметр внутреннего треугольника меньше внешнего. Сторона АВ общая для этих треугольников
Какой вывод из этого можно сделать?	АВ – основание треугольников АВС и АВМ.
Какое существует теоретическое положение, связывающее стороны треугольника?	Сумма двух смежных сторон треугольника всегда меньше третьей
Выразите сторону АВ используя это теоретическое положение для треугольников АВС и АВМ	АВBC+AC АВ	ΔАВМ и Δ АВС ΔАВМΔ АВС АВBC+AC АВ
Вы сделали вывод о том, что длины сторон внутреннего треугольника меньше внешнего. Как в этом случае можно записать неравенство	Т.к. ВМAMAC, то и их сумма будет также меньше суммы двух соответствующих сторон большего треугольника	АС+ВСАМ+ВМ
Рассмотрите другу пару треугольников.	Рассмотрим треугольники АВС и МВС.	ΔСВМ и Δ АВС ΔСВМΔ АВС СВBА+AC СВ ВА+АСВМ+СМ
	Аналогично рассмотрим треугольники АВС и АМС	ΔСАМ и Δ АВС ΔСАМΔ АВС САBА+ВC СА ВА+ВСАМ+СМ
Сложите получившиеся неравенства		АС+ВСАМ+ВМ + ВА+АСВМ+СМ ВА+ВСАМ+СМ 2(ВА+ВС+АС)2(АМ+СМ+ВМ)
Что вы можете сказать о левой и о правой частях неравенства?	Левая и правая часть неравенства имеет один и тот же коэффициент «2». В скобках записана формула периметра треугольника.
Упростите неравенство		РAM+CM+BM
Еще раз прочитайте условие задачи.
Какие выводы Вы можете сделать?	Задача решена.
Чем интересна эта задача?	Зная, что периметр треугольника всегда больше суммы отрезков (расстояний) от произвольной точки внутри треугольника до его вершин можно решать различные задачи, используя этот факт.