МВД России
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ КАЗЕННОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЕЛАБУЖСКОЕ СУВОРОВСКОЕ ВОЕННОЕ УЧИЛИЩЕ
МИНИСТЕРСТВА ВНУТРЕННИХ ДЕЛ РОССИЙСКОЙ ФЕДЕРАЦИИ»
(Елабужское суворовское военное училище МВД России)
СЦЕНАРИЙ УРОКА по предмету «Математика»
для обучающихся (суворовцев) 3 курса (XI класс)
по теме «Площадь криволинейной трапеции»
Время – 45минут
Учебник: Алгебра и начала математического анализа. 10 – 11 классы: учебник для общеобразовательных учреждений / А.Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под ред. А.Н. Колмогорова. – 19-е изд. – М.: Просвещение, 2010. – 384 с.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Необходимым условием успешной учебной деятельности обучающихся, на мой взгляд, является интерес к изучаемому предмету, потребность понимания. На основе интереса происходит мобилизация внимания, стремлений, чувствительного и мыслительного восприятия. В каждом учебном заведении эта проблема решается по-своему.
Методическая тема нашего училища тесно связана с профориентацией воспитанников. Поэтому я, на уроках математики рассказываю будущим сотрудникам МВД о применении математики в ходе своей будущей службы, о том, что глубокие знания точных наук необходимы для овладения основами многих профессий сотрудников внутренних дел. Тематическая направленность курса математики решает проблему воспитания интереса у суворовцев к изучаемому материалу, формирует профессиональные знания. Сейчас мы работаем с ребятами над составлением собственного сборника задач тематической направленности по заданиям ЕГЭ.
Сценарием этого урока, я хочу показать лишь один подход в организации занятия, дающий возможность использовать процесс обучения математики и в патриотическом воспитании обучающихся, и в профессиональном.
Урок – клеточка педагогического процесса.
В нем, как солнце в капле воды, отражаются все его стороны.
Если не вся, то значительная часть педагогики концентрируется в уроке.
Скаткин М.
Цели:
образовательные:
обобщить и систематизировать знания о площади, а также знания формул для вычисления площади основных геометрических фигур;
обеспечить усвоение обучающими понятия новой геометрической фигуры – криволинейной трапеции;
способствовать усвоению формулы для вычисления площади криволинейной трапеции;
развивающие:
воспитательные:
обеспечить условия развития логического мышления, грамотной математической речи, аккуратности при построении чертежей; умения слушать товарища; организованности и сосредоточенности, положительного отношения к учебной деятельности.
Задачи урока:
развитие познавательного интереса к предмету;
воспитание самостоятельности, настойчивости при достижении конечного результата.
формирование культуры учебной деятельности и информационной культуры;
обеспечить повторение основных понятий.
Ход урока
Организационный момент. (1 мин)
Приветствие суворовцев. Чем мы занимались на предыдущем уроке? На последних уроках алгебры мы находили первообразные функций. Так вот, сегодня на уроке мы узнаем, как можно использовать первообразную для нахождения площади криволинейной трапеции. Какой вопрос вы хотите мне задать? Правильно, а что такое криволинейная трапеция?
Слайд 1. Откройте тетради, запишите сегодняшнее число, слова «Классная работа» и тему урока «Площадь криволинейной трапеции». Разбираем тему урока по словам. С понятием площади мы давно знакомы и умеем находить площади различных фигур. Каких? Площадь треугольника, трапеции, параллелограмма, прямоугольника, ромба, круга и др.
Актуализация знаний. (3 мин)
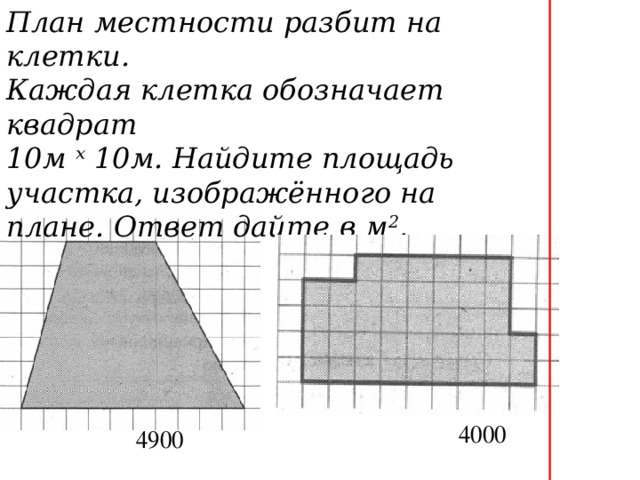
Слайд 2, 3. Раз так, то я предлагаю вам вычислить площади представленных вам фигур. Назовите только ответ. По какой формуле вычисляли? Ребята, верно, называют ответы и приводят формулы, по которым вычисляли. Здесь необходимо обратить внимание обучающихся на единицы измерения и на вопрос в условии задачи на Слайде 2: 6 – чего? 12 – чего? 6 – чего? 7,5 – чего?
на Слайде 3: 4900 – чего? 4000 – чего? В решении этих задач возможны ошибки 49 и 40. Указать, почему неверно. И еще, я всегда, задаю вопрос: Сколько клеточек для записи ответа вам потребуется в экзаменационных бланках ответов?
Слайд 4. Хочу представить вашему вниманию задачу, придуманную суворовцами 2 курса: Плац в военной части разбит на клетки. Каждая клетка обозначает квадрат 5м на 5м. выделенная часть плаца – сцена. Найдите площадь плаца (без учёта сцены), которую можно использовать для строевой подготовки. Ребята рассказывают, как считали. Называют ответ 58. 58 чего? А теперь найдите площадь в квадратных метрах? Как? Скажите, а какое свойство площадей мы использовали? Если дети не могут его сформулировать, то можно предложить: «Давайте я начну, а вы продолжите: Если фигура разбита на части, то её площадь равна… сумме площадей её частей».
Постановка проблемы. (9 мин)
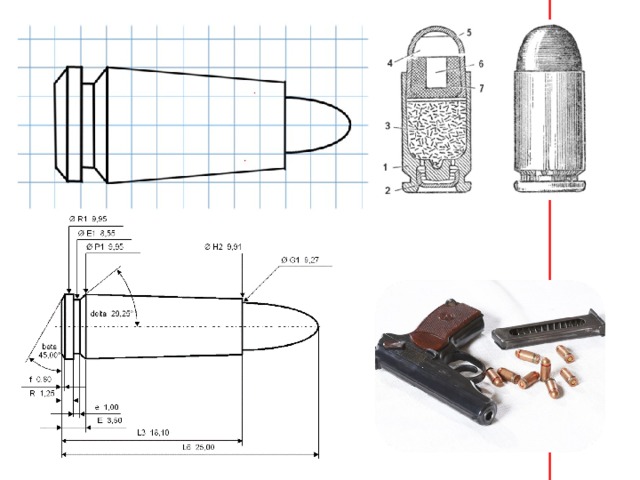
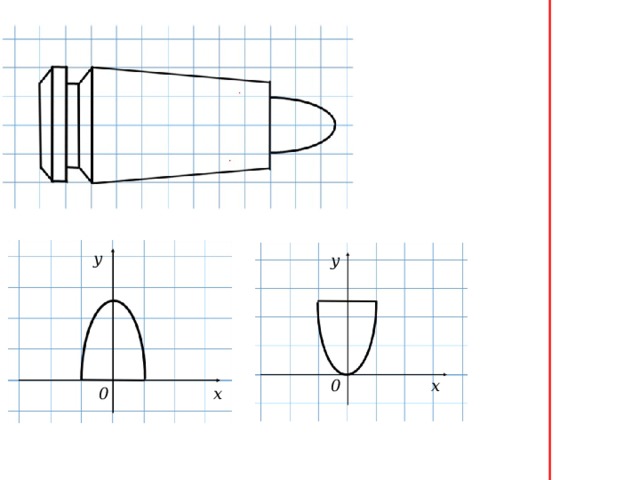
Это была ваша задача, а теперь моя: я вот нарисовала такую фигуру Слайд 5. И прошу вас найти её площадь, но прежде чем приступить к этому, мне очень хотелось узнать хороший ли я художник? На что похожа моя фигура? Что она вам напоминает? Ребята, конечно же, сразу её узнали, я назвала её пулей, но они меня тут же поправили – это патрон. По рисункам, которые появляются по щелчку, ребята рассказали: из чего состоит патрон, какие бывают патроны по виду оружия, по типу снаряда, по назначению, где применяют. Суворовцы много знают об оружии, поскольку у них преподаётся предмет военная подготовка и их это интересует. А теперь вернёмся к моему патрону и найдем её площадь. Снова по щелчку рисунки растворяются, и остаётся патрон. Тут же ими было замечено, что разбить на фигуры можно и вычислить площади этих частей тоже можно, кроме закругленной части, которая как раз и называется пулей. У нас встречались задачи, в которых можно было увидеть по клеточкам окружность или её часть и попытаться найти площадь, поэтому ребята сначала пытались это сделать, но безрезультатно, тогда сказали, что не могут и предположили: это и есть, наверно криволинейная трапеция.
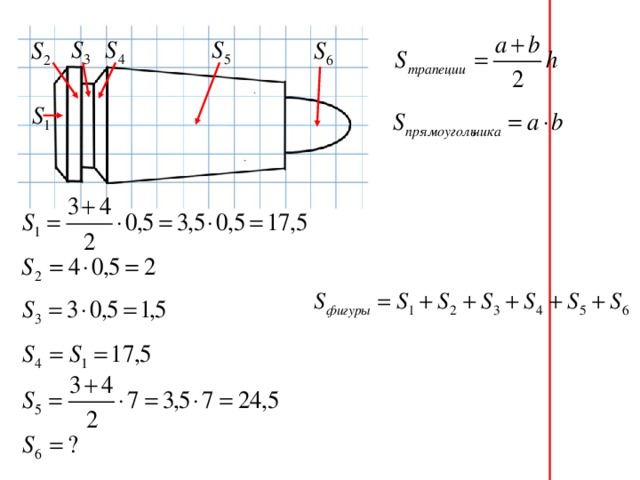
Слайд 6. Мы вместе разбили фигуры на части и обучающиеся нашли площади этих частей, сверили с доской. Тогда давайте узнаем, что же такое криволинейная трапеция.
Ведение понятия криволинейная трапеция. (4 мин)
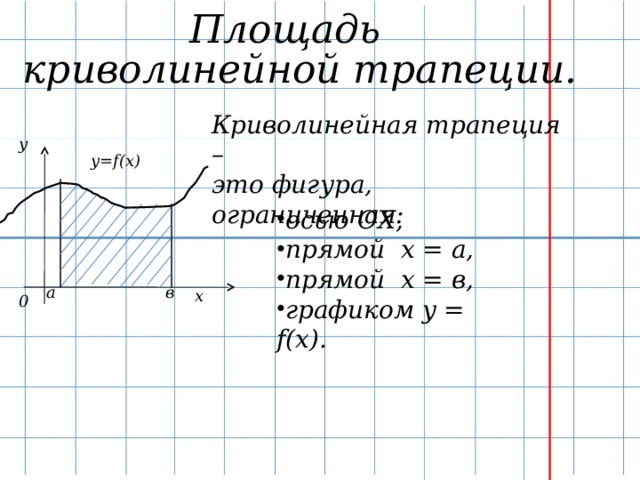
Слайд 7. Строя рисунок к определению, я проговариваю, после чего предлагаю им самим попытаться записать схему этого определения. Криволинейной трапецией называют часть плоскости, ограниченную осью ОХ, прямыми х = а, х = в и графиком неотрицательной на отрезке [a;b] функции y = f(x).
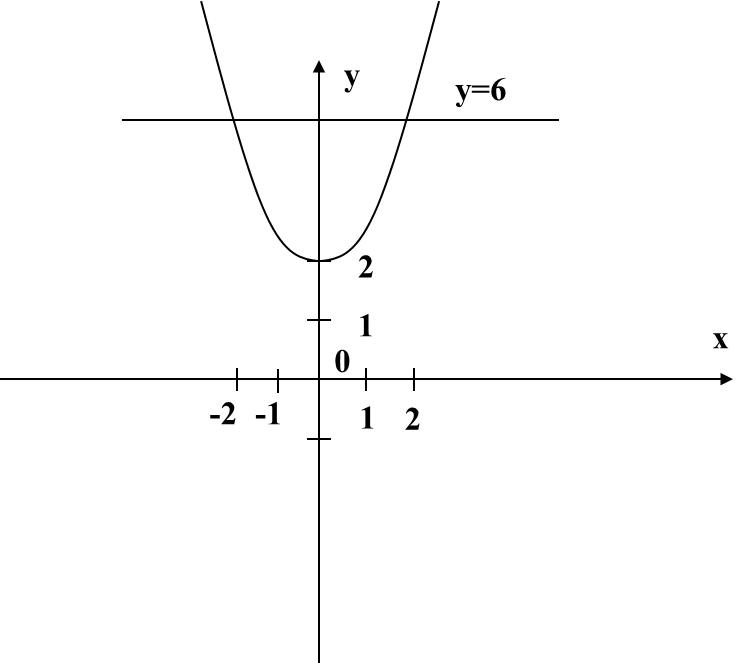
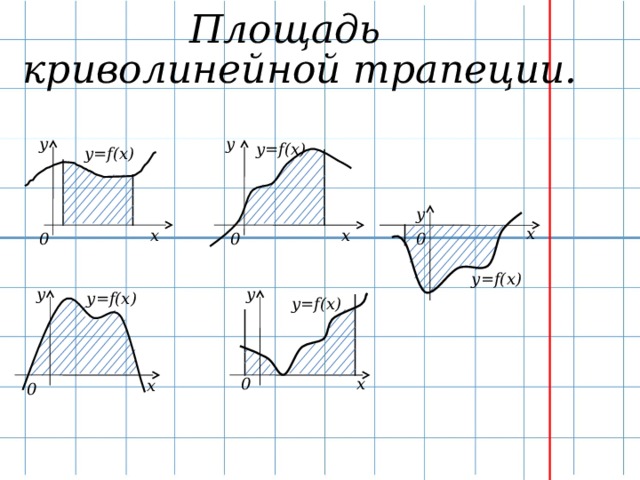
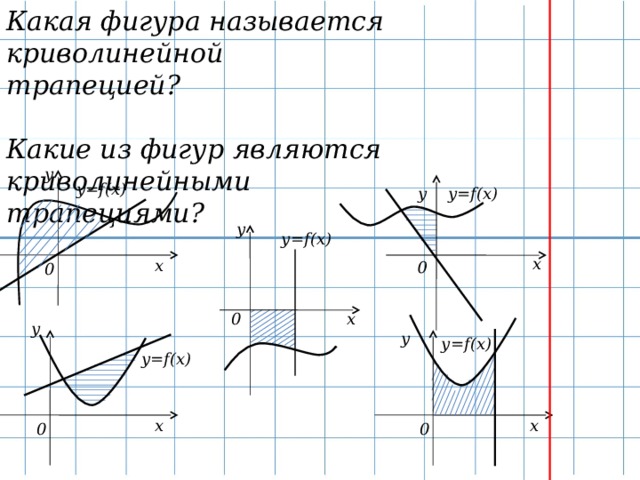
Слайд 8. Приведу примеры криволинейных трапеций. Докажите, что каждая из них является криволинейной трапецией (по определению).
Закрепление определения криволинейной трапеции. (7 мин)
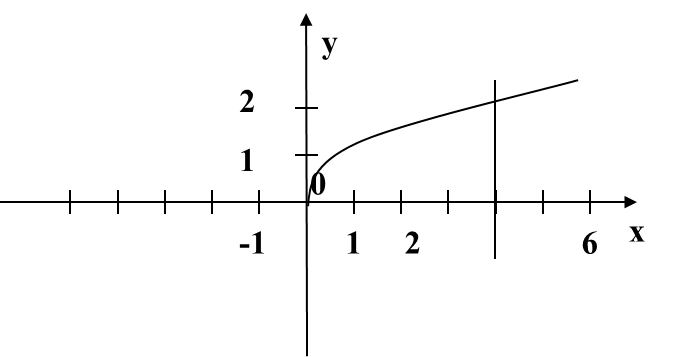
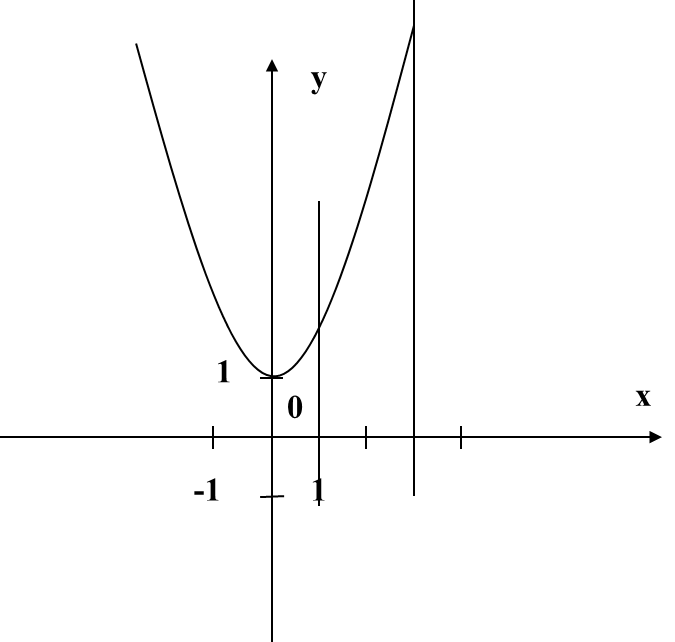
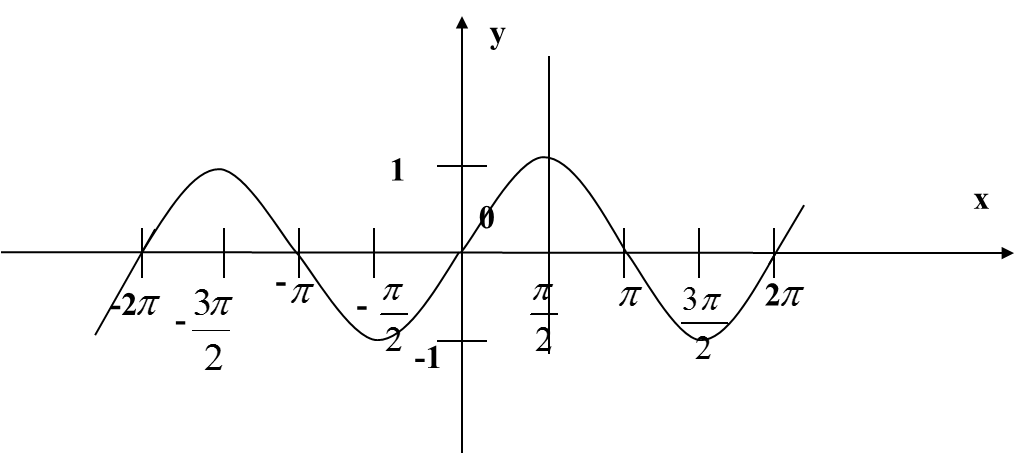
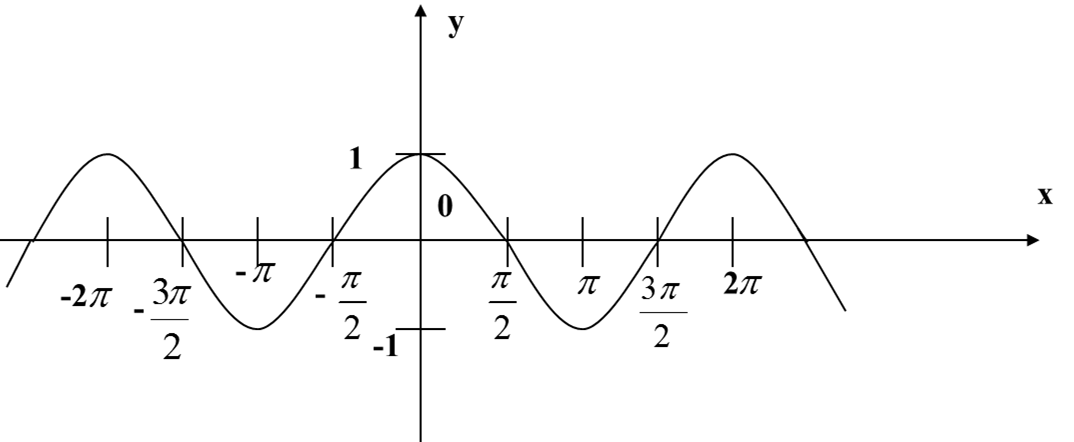
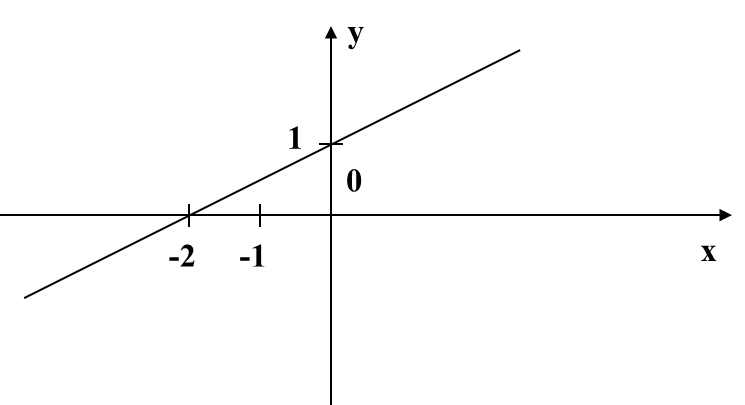
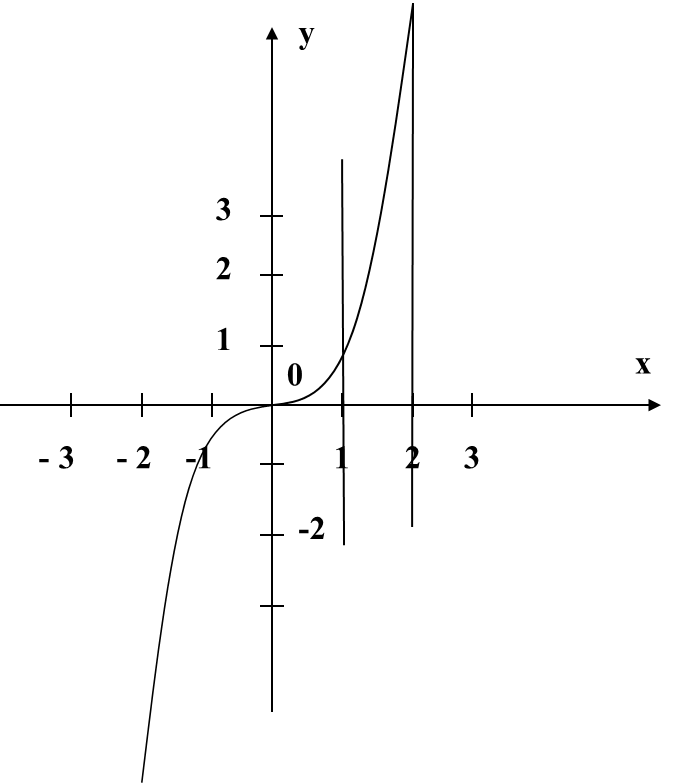
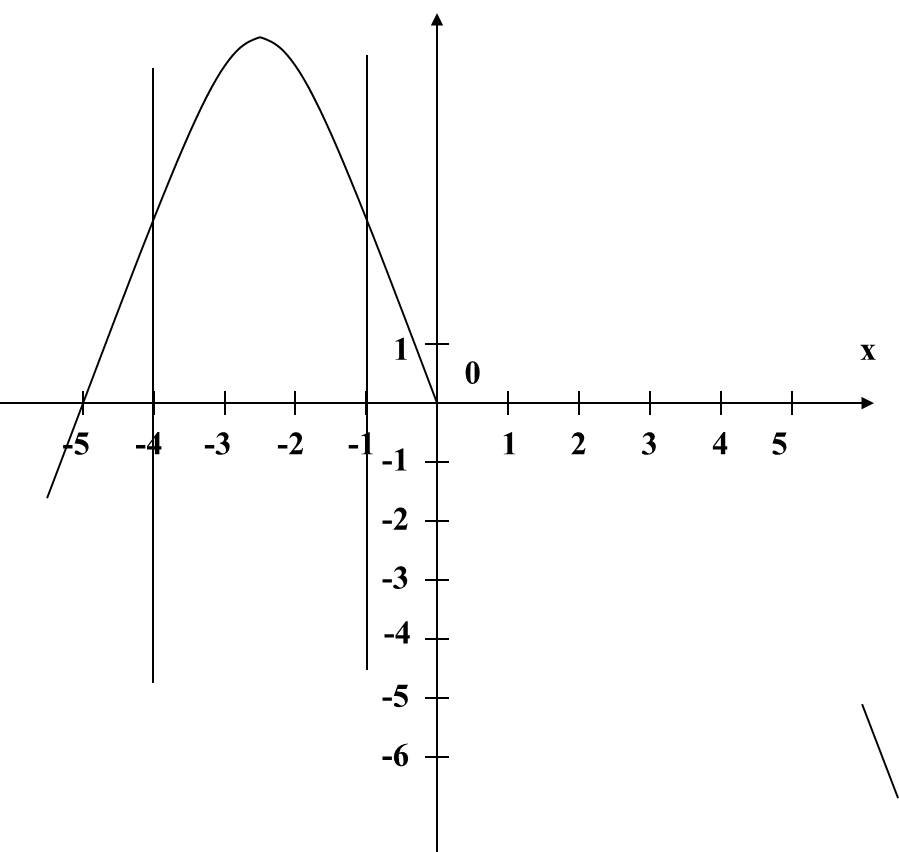
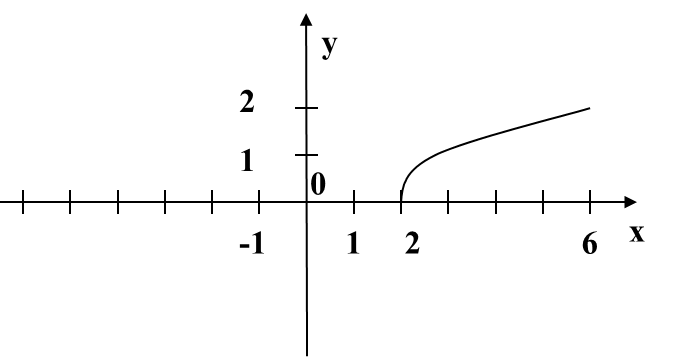
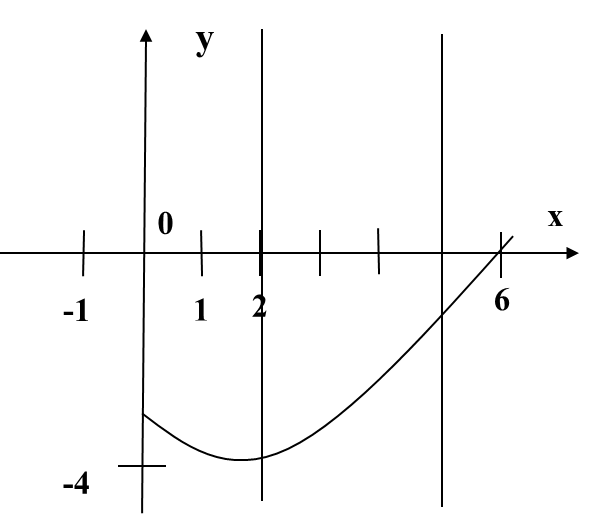
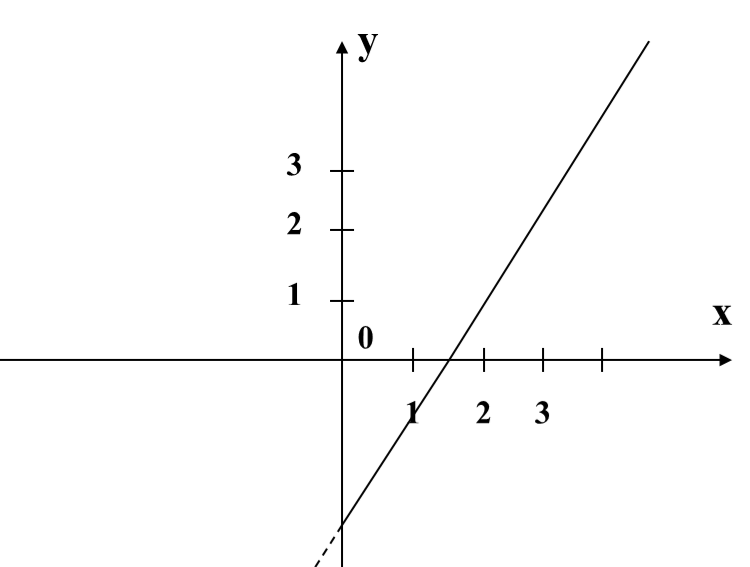
На листочках (Приложение 2), что видим? Верно, знакомые графики функций. Ставлю перед вами следующую задачу: найдите и заштрихуйте криволинейные трапеции, т.е. ваши заштрихованные фигуры должны соответствовать определению. Нужно пользоваться схемой определения и доской. Поменялись листочками, проверили, если возникнут вопросы, поднимите руку. Вы заметили, что у некоторых получились разные заштрихованные фигуры, но они соответствуют определению. В нашем случаи такое быть могло, потому что я не дала вам конкретные границы, а и в и вы какую увидели, такую и выделили. Какую выделили, площадь такой криволинейной трапеции находить и будете. Вопрос? А как? Прежде, чем я вам на него отвечу, давайте вернемся к моему патрону
Слайд 9. Нам надо часть патрона, а именно, площадь которой мы не можем найти, расположить в системе координат. Какое расположение вы выбираете? Выбираем более удобное.
Работа с учебником по теореме о площади криволинейной трапеции. (3 мин)
Что такое криволинейная трапеция вы уяснили, а вот как её найти вы пока не знаете. Предлагаю открыть учебник на стр. 186 найдите теорему о площади криволинейной трапеции, прочитайте его и запишите в тетрадь: Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b], т. е. S = F(b) – F(a). После этого вместе проговариваем и выделяем формулу S = F(b) – F(a). Что значит F в этой формуле? А F(b)? F(a)? Получается, что надо вспомнить, как находятся первообразные некоторых функций.
Задание на нахождение первообразной. (4 мин)
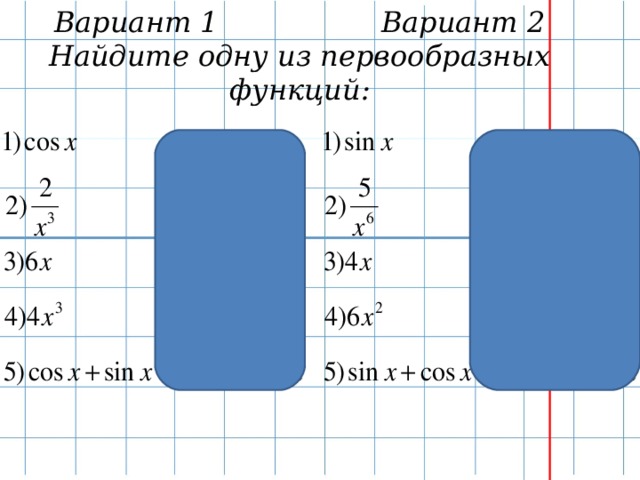
Слайд 10. Найдите одну из первообразных функции, по вариантам в тетрадях. Ответы открываются и взаимопроверка. Задания, в которых допущены ошибки, необходимо решить у доски с полным комментированным ответом, теми, кто справился.
Закрепление формулы нахождения площади криволинейной трапеции. (11 мин)
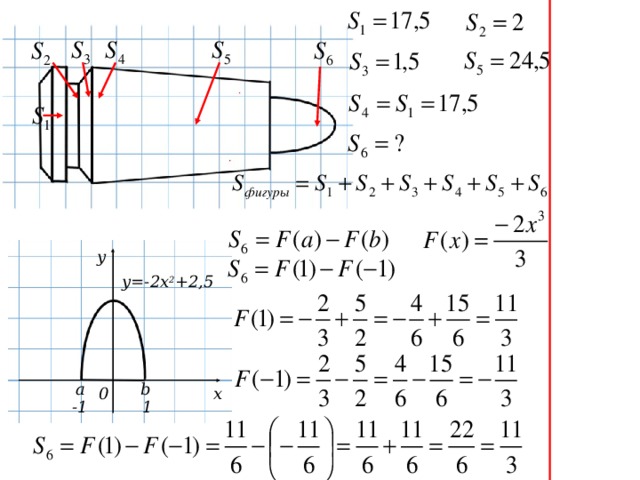
Слайд 11. Итак, теперь мы знаем, по какой формуле находится площадь криволинейной трапеции, поэтому, давайте, вместе вычислим площадь пули в моем патроне. Мы уже нашли S1, S2, S3, S4, S5. Не смогли вычислить S6 . По какой формуле будем вычислять? Значит, чтобы вычислить S6, необходимо найти первообразную функции. Первообразную какой функции будем искать? Уравнения функции нет, попробуем задать его по графику. На график, какой функции похожа наша кривая? Верно, парабола, ветви направлены вниз, через какую точку проходит? Совсем немного потребуется времени, чтобы обучающиеся назвали уравнение параболы
у = – 2х2 + 2,5. Чему равна одна из её первообразных? Чему равны а и b? Значит, как будет выглядеть формула для вычисления S6? Предлагаю отдельно вычислить F(1) и F(–1). Проверим с доской. Ответы на все мои вопросы по щелчку появляются на слайде. Подставим в формулу и найдем S6.
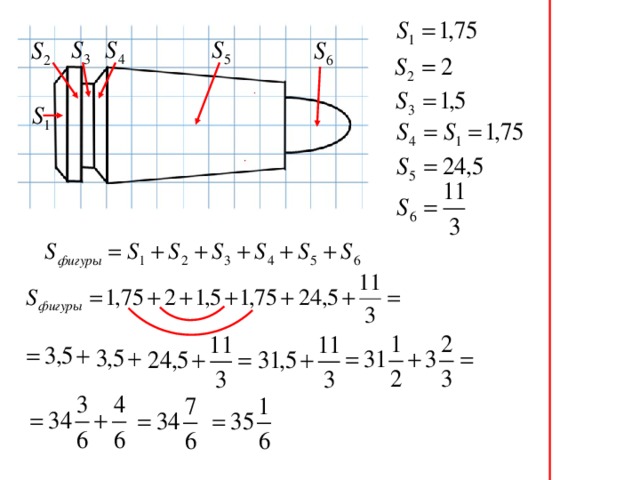
Слайд 12. Вычислите площадь всего патрона. Как будем считать Sфигуры? Ответ? Вычисления можно проверить на доске.
На листочках (Приложение 2), вычисляем площади тех криволинейных трапеций, которые вы выделили. Какую формулу будете применять? Что сначала необходимо найти? Что такое а и b? Приступайте. Ребята выполняют задание, задают вопросы, я – прохожу по рядам и помогаю, если это необходимо.
Подведение итога урока. (2 мин)
Подведение итога урока можно организовать по вопросам
Слайда 13. После чего, можно предложить закончить предложение: Фигура не является криволинейной трапецией, если:……….
ни одна ее сторона не лежит на оси ОХ;
она ограничена графиками нескольких функций;
вся фигура или ее часть располагаются ниже оси ОУ.
Как находить площадь таких фигур, мы узнаем на следующем уроке.
Домашнее задание. (1 мин)
Доделать задание на листочках (Приложение 2), то есть вычислить площади всех выделенных вами криволинейных трапеций.
Оборудование урока: интерактивная доска,
презентация (Приложение 1),
раздаточный материал (Приложение 2),
учебник: Алгебра и начала математического анализа. 10 – 11 классы: учебник для общеобразовательных учреждений / А.Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под ред. А.Н. Колмогорова. – 19-е изд. – М.: Просвещение, 2010. – 384 с.