Просмотр содержимого документа
«разработка урока-графическое решение систем уравнений»
МОУ СОШ №20 г.Владивостока

Преподаватель:
Омельченко Т.М.
Цель:
создать условия для усвоения и применения умений и навыков к исследованию функции при решении уравнении и систем уравнении графическим способом;
формирование способности учащихся к поиску новой учебной информации.
Задачи: отработка УУД:
познавательные:
регулятивные:
развивать навыки самоконтроля,
развивать навыки и умения применения компьютеров,
уметь делать выводы,
личностные:
уметь работать в группах, совещаясь,
уметь слушать, вступать в диалог.
Обеспечение:
| Этапы урока | Деятельность учителя | Деятельность учащихся |
| Сообщение темы урока, целей урока. Проблемные вопросы | Исходя из целей урока сегодня предстоит выявить, как связаны решения систем уравнении с графиками функции? От чего зависит решение систем? | Ответы. Предложения. Идеи. |
| Актуализация опорных знаний, умений
ИТОГ | Устная работа по учебнику стр.64, рис.26. а)наибольшее значение функции б)значения х, при которых у0, y в)значения х, при которых у=-5, у=0 ИТОГ: при аналитическом решении точки х1 и х2 -это точки пересечения с осью ОХ | Отвечают устно по рис.26. Интерактивная доска.
Корни уравнения у=0
|
| Подготовитель-ный этап: проблема, диалог.
Итог-идея | Сколько точек пересечения имеет график квадратичной функции и график прямо пропорциональной зависимости? Гиперболы и параболы? От чего зависит количество точек пересечения графиков функции? | Примеры по интерактивной доске
Ответ: От взаимного расположения графиков |
| Проблема: | Сколько различных видов расположения графиков двух функции? Три случая и рассмотрим | Возможны три случая |
| Исследование в группах по технологической карте на компьютере: Работа в таблице
| Следит за построением графиков уравнений- решением систем графическим способом
Следит за работой по таблице. Работая в группах, общаясь, заполняйте таблицу, отвечая на вопрос: «Сколько решений имеет система уравнений?» | Работают на компьютере, заполняя таблицу Приложение 1 Приложение 2
Готовят вывод по таблице |
|
Работа в трёх группах- общий вывод
Рефлексия
Домашнее задание | Следит за обоснованием ответов по каждому случаю. Следит за четким пониманием и усвоением трёх случаев решения систем уравнений Сколько решений может иметь система уравнений? Следит за общением и подготовкой к ответу - общему выводу.
Сколько решений может иметь система уравнений в зависимости от трёх случаев?
Решить системы уравнений аналитически из таблицы, №208,часть2 | Приложение 3 Объясняют решения по экрану, отвечая на главный вопрос Заполняют таблицу Работают в группах Представитель группы отвечает вывод на главный вопрос.
Отвечают: одно, т.е. целое число решений, не иметь решений, множество решений Записывают домашнее задание |
| Защита презентаций учащихся «Решение систем уравнений графическим способом». | Координирует ответы на вопросы презентации | Ученики комментируют презентацию: «Функция. Решение систем уравнений графическим способом» |
| Дополнительно №208 |
|
|
| Рефлексия. |
|
|
Ход урока:
1.Задачи и цели урока:
Повторение свойств квадратичной функции, решение уравнений и систем уравнений графическим способом, составление таблицы.
Уметь делать выводы.
2. Устные упражнения по интерактивной доске
Работа по учебнику (стр.64, рис.26):
а) определить наибольше значение функции
б) значения х, при которых у0,
y
в) значения х, при котором у=-5.
3.Подготовительный этап
а) Сколько точек пересечения имеет окружность и прямая?
б) Сколько точек пересечения имеет парабола и прямая?
в) Сколько решений имеет система уравнений, состоящая из уравнения квадратичной функции и гиперболы?
4.Работа по технологической карте в группах на компьютере с последующим объяснением у экрана
см. Приложение 1
5.Заполнение таблицы
см. Приложение 2
6.Вывод
Система уравнений может иметь…
7.Рефлексия:
Сколько решений может иметь система уравнений с двумя переменными?
8.Домашнее задание:
Решить аналитически системы, записанные таблице №208, 121.
9.Дополнительно:
Решить графически №208,стр.121.
10.Показ презентации
«Функция. Решение систем уравнений с двумя переменными графическим способом»
Приложение 1
Технологическая карта
Задание №1 Решить графически систему уравнений
1.Запустить программу Пуск/ Программа/Advancer Grapher.
2.Нажмите кнопку  ( Добавить график ).
( Добавить график ).
3.В поле Формула наберите обязательно английскими буквами формулу _________________.
4.Установите самостоятельно толщину линии и цвет линии.
5.Подтвердите ввод кнопкой Ок.
6. Нажми кнопку Добавить график.
7. В поле формула набери ______________.
8.Подтвердите ввод кнопкой Ок.
9. Ответь на вопрос:
Приложение 2
Сколько решений имеет система уравнений с двумя переменными?
| 1 случай
| Ответ | 2 случай | Ответ | 3 случай | Ответ |
| Условие задания
|
| Условие задания |
| Условие ззадания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| вывод
|
| вывод |
| вывод |
|
Общий вывод: система уравнений может иметь…
Приложение 3
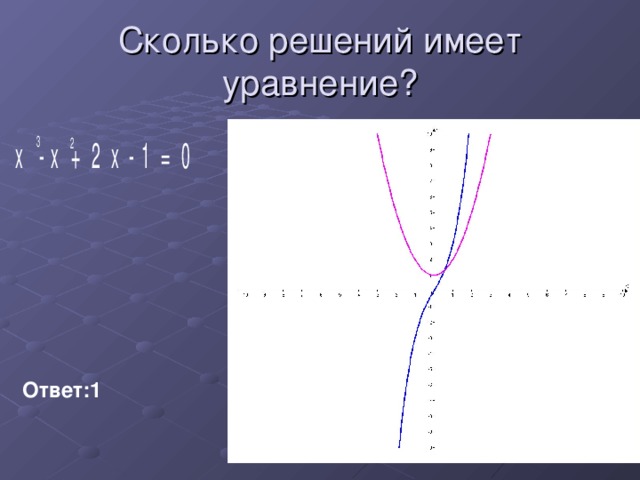
Сколько решений имеет система уравнений 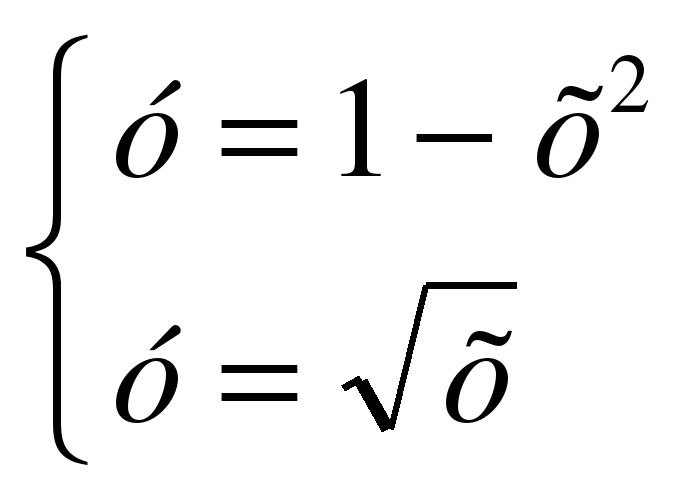 ?
?
1 случай
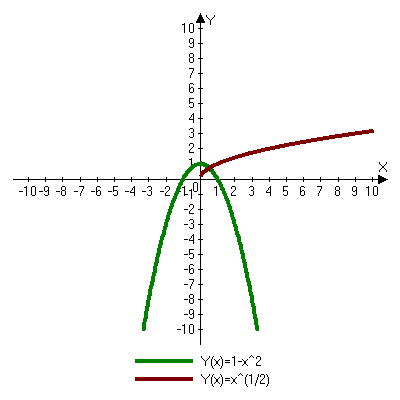
Ответ: одно решение
Решить графически 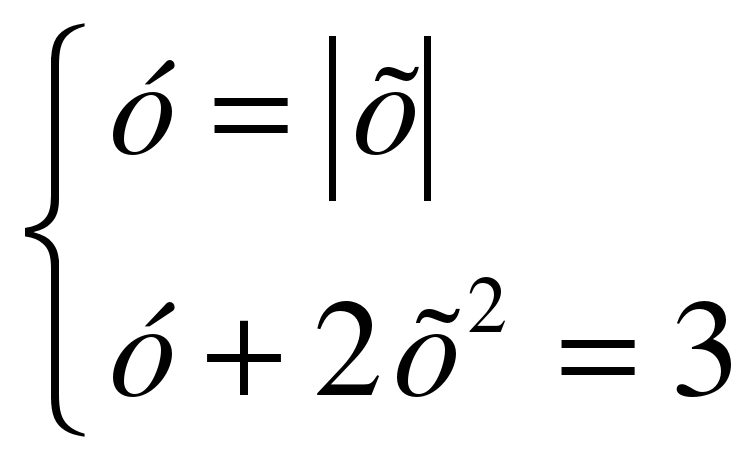
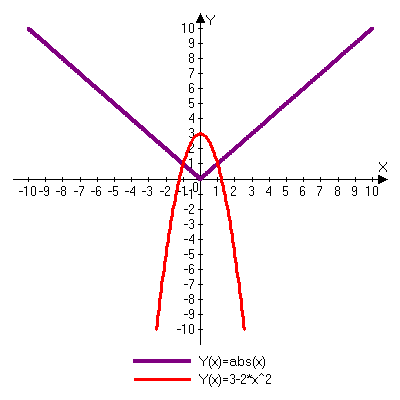
Ответ: два решения (-1;1), (1;1)
Сколько решений имеет система уравнений 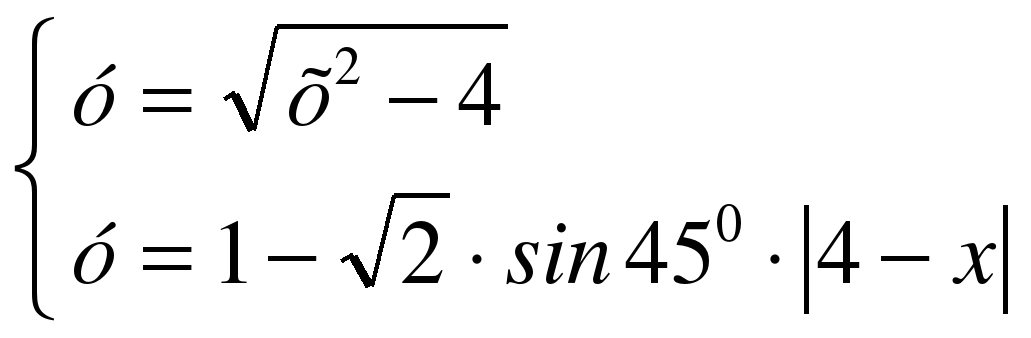 ?
?
2 случай
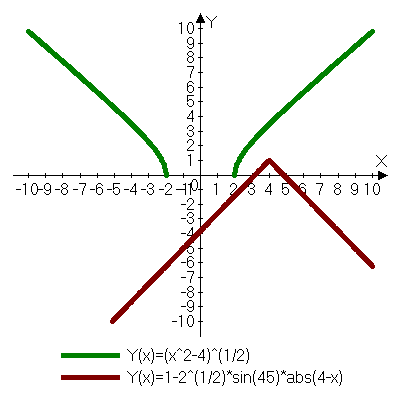
Ответ: нет решений
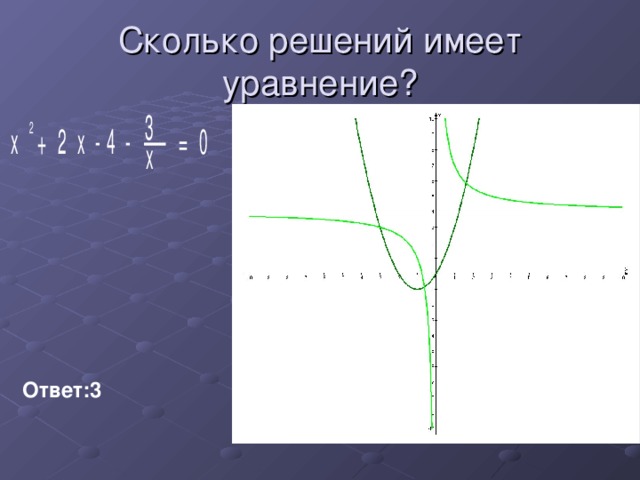
Сколько решение имеет система уравнений 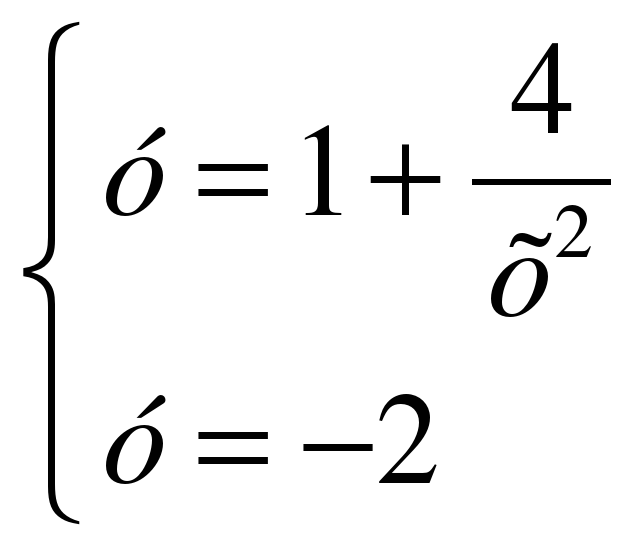 ?
?
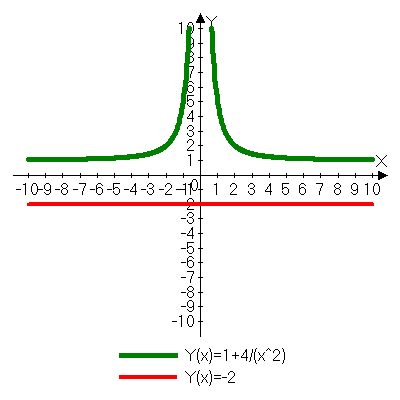
Ответ: нет решений
3 случай
Сколько решений имеет система уравнений 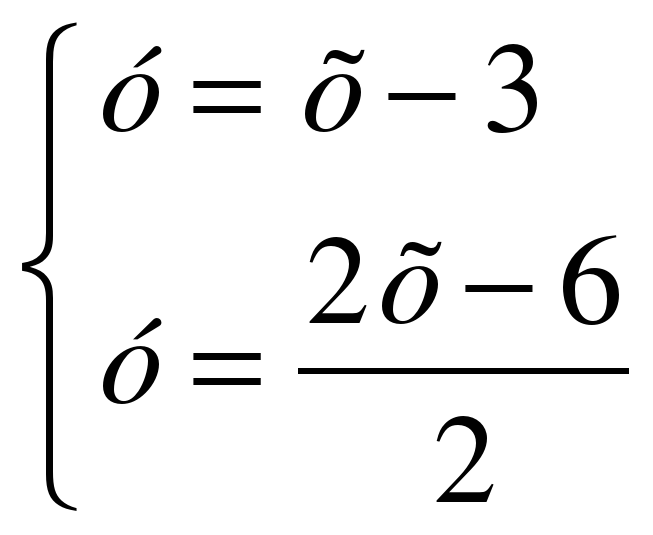 ?
?
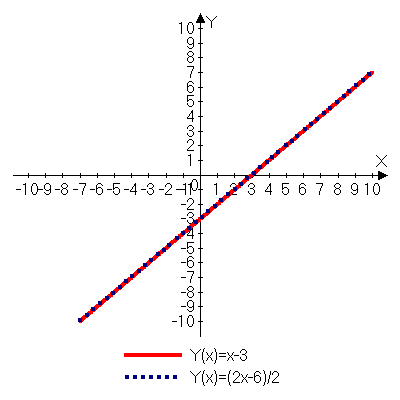
Ответ: множество решений
Просмотр содержимого презентации
«Степанова Вика»
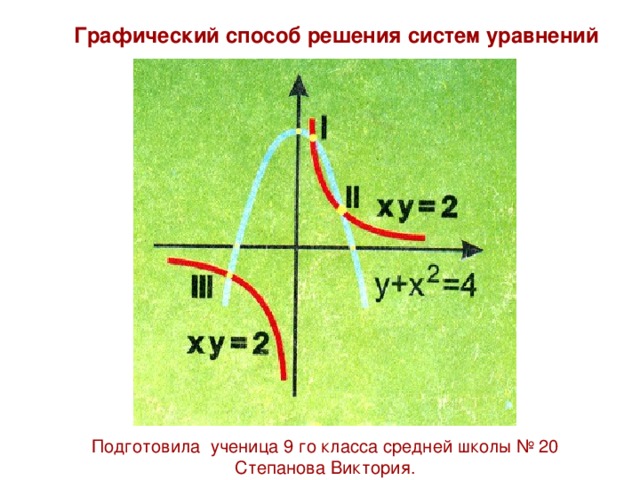
Графический способ решения систем уравнений
Подготовила ученица 9 го класса средней школы № 20
Степанова Виктория.

Конечно, Вам придется иметь дело с уравнениями попроще, и, тем не менее, графики их нужно уметь строить.
!
А теперь к делу – учимся решать системы уравнений с двумя переменными графически!
!
?
Уравнение 1,
Уравнение 2;
Дальше
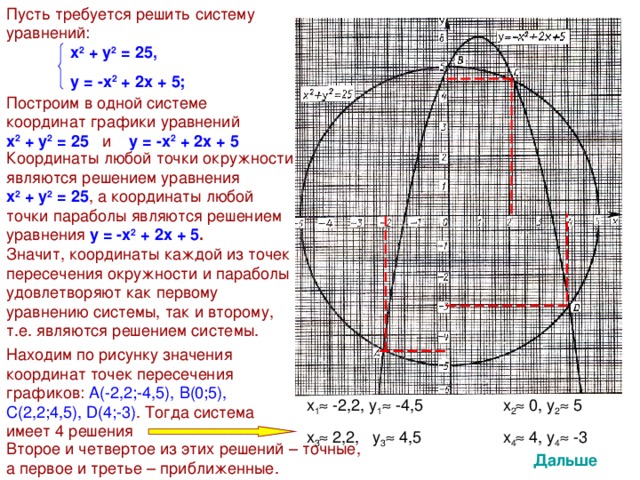
Пусть требуется решить систему уравнений:
х 2 + у 2 = 25,
у = -х 2 + 2х + 5;
Построим в одной системе координат графики уравнений
х 2 + у 2 = 25 и у = -х 2 + 2х + 5
Координаты любой точки окружности являются решением уравнения х 2 + у 2 = 25 , а координаты любой точки параболы являются решением уравнения у = -х 2 + 2х + 5 .
Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы.
Находим по рисунку значения координат точек пересечения графиков: А(-2,2;-4,5), В(0;5),
С(2,2;4,5), D (4;-3) . Тогда система имеет 4 решения
1 1 2 2
3 3 4 4
Второе и четвертое из этих решений – точные,
а первое и третье – приближенные.
Дальше

Давайте сделаем из рассмотренного примера выводы.
Чтобы решить систему двух уравнений с двумя неизвестными, нужно:
- Построить в одной системе координат графики уравнений, входящих в систему;
- Определить координаты всех точек пересечений графиков (если они есть);
- Координаты этих точек и будут решениями системы.
Помните о двух вещах!
- Если точек пересечения графиков нет, то система решений не имеет;
- Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными;
Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!
Дальше
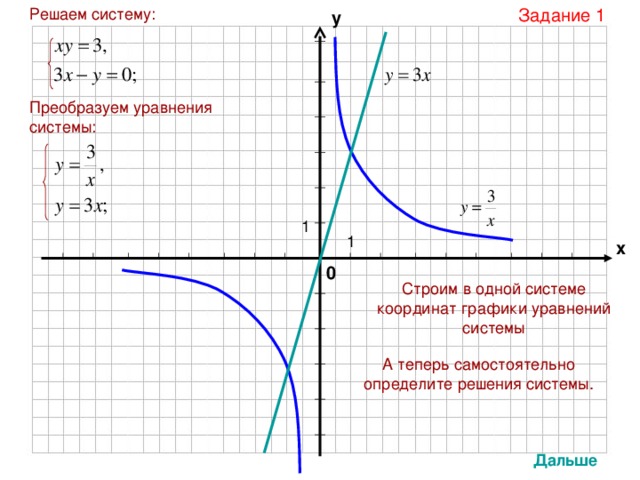
Решаем систему:
Задание 1
у
Преобразуем уравнения системы:
х
0
Строим в одной системе координат графики уравнений системы
А теперь самостоятельно определите решения системы.
Дальше
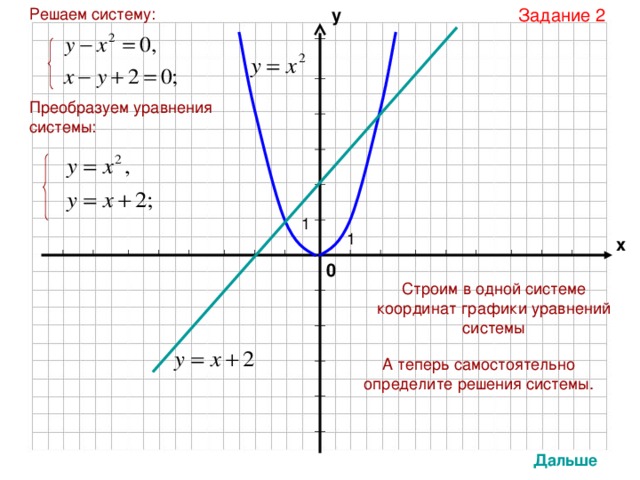
Задание 2
у
Решаем систему:
Преобразуем уравнения системы:
х
0
Строим в одной системе координат графики уравнений системы
А теперь самостоятельно определите решения системы.
Дальше
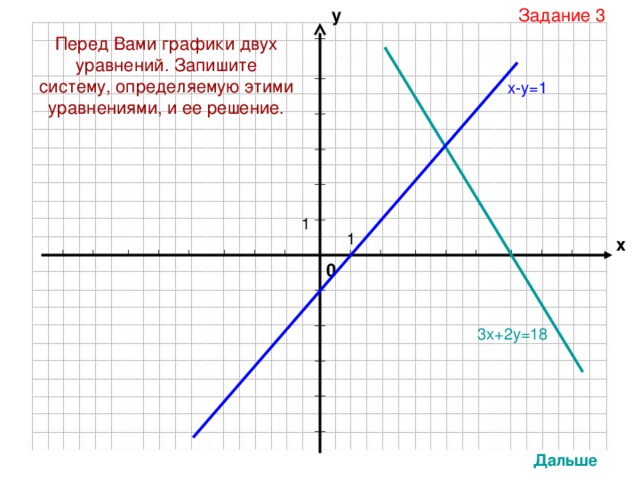
у
Задание 3
Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение.
х-у=1
х
0
3х+2у=18
Дальше
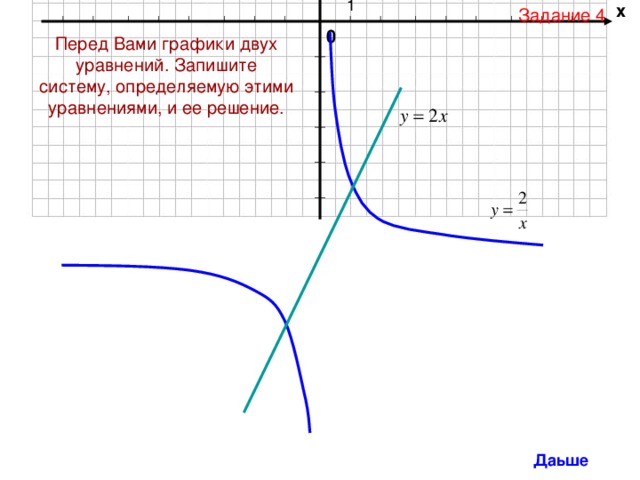
у
х
Задание 4
0
Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение.
Даьше
л
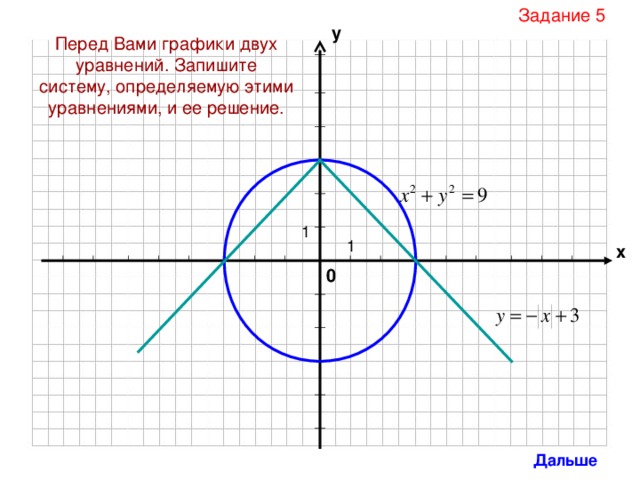
Задание 5
у
Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение.
х
0
Дальше
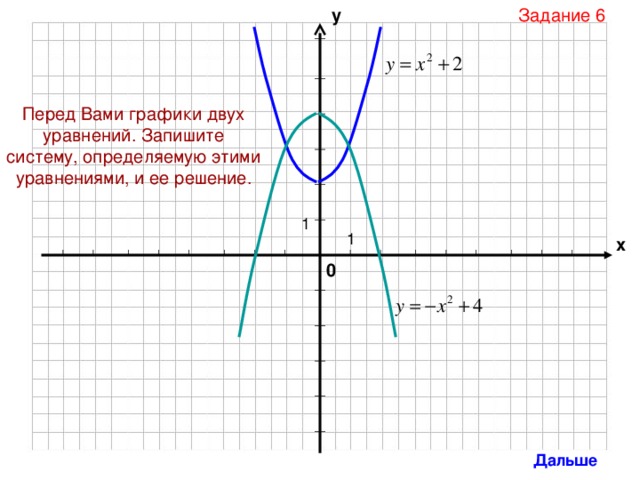
Задание 6
у
Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение.
х
0
Дальше
у
0
Просмотр содержимого презентации
«Шерстнёв Иван»

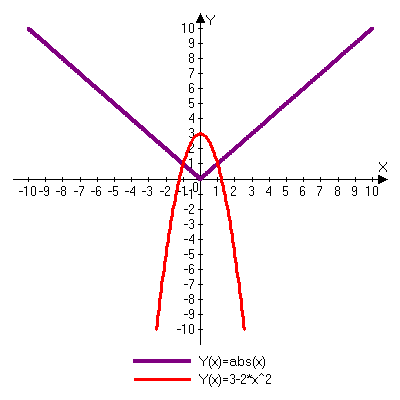

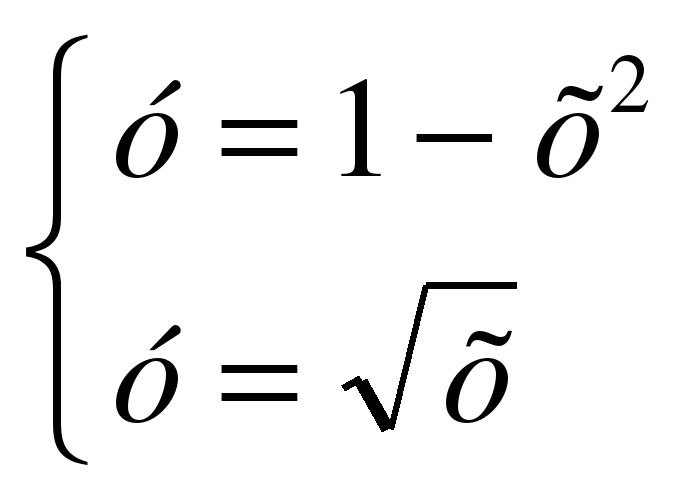 ?
?
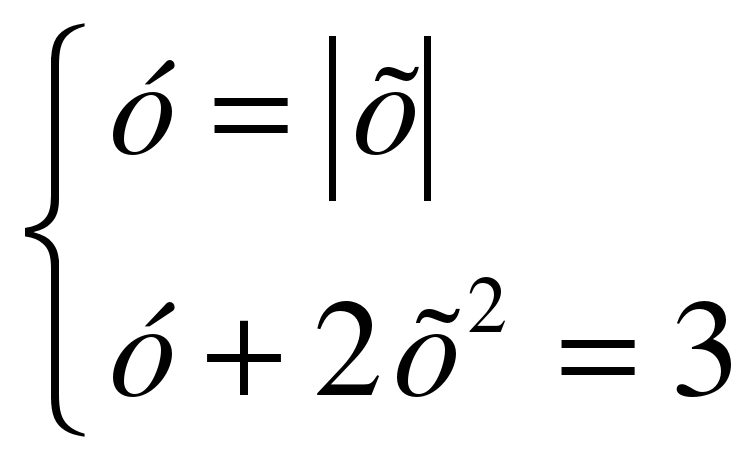
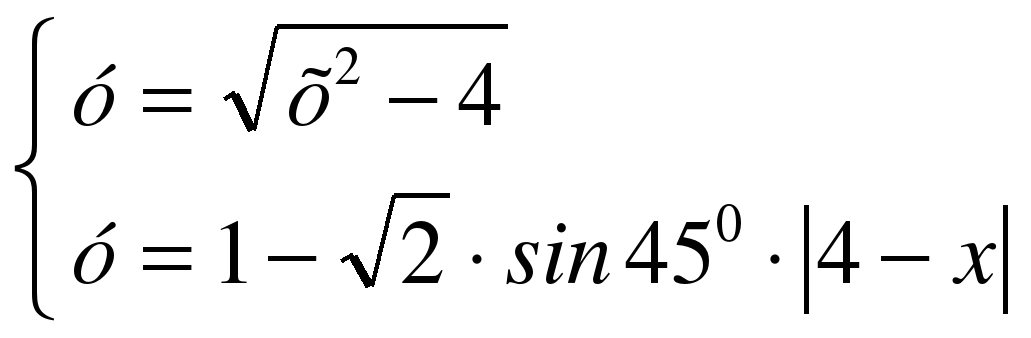 ?
?
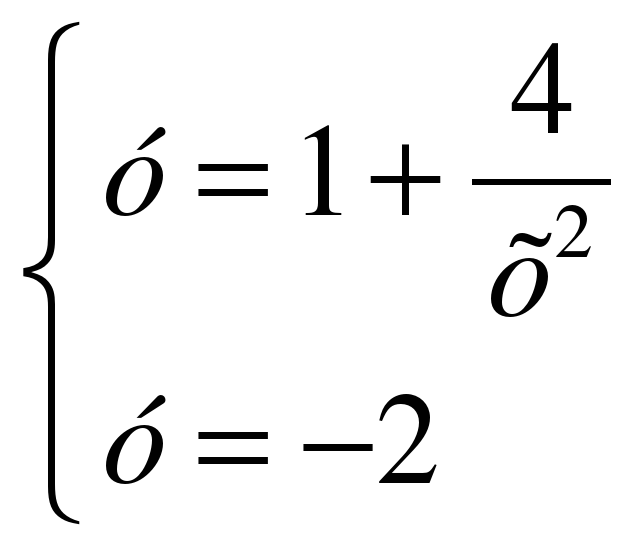 ?
?
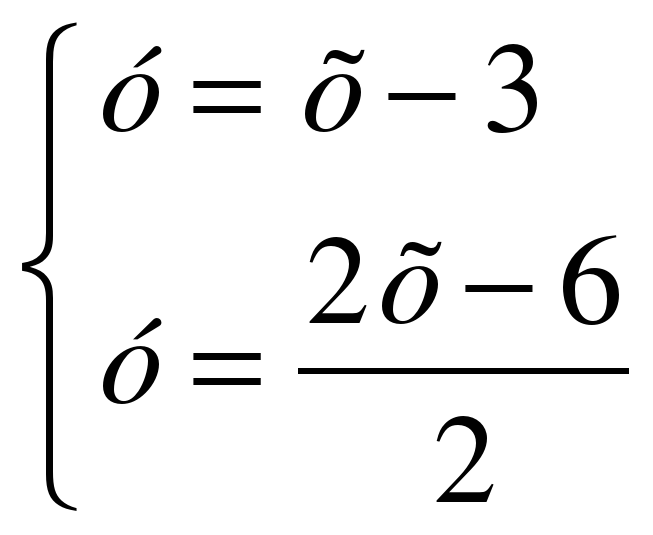 ?
?