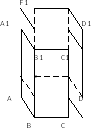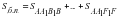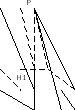|
Деятельность учителя На сегодняшнем уроке мы с вами поговорим о геометрических телах. На какие группы можно разделить все геометрические фигуры (Учитель показывает натуральные модели плоских тел: треугольник,квадрат, пятиугольник, n-угольник и пространственных тел; куб, тетраэдр, пирамида, призма). На какие 2 вида можно разделить плоские геометрические фигуры? (Учитель показывает натуральные модели многоугольников и немногоугольников). Попробуйте описать многоугольник, что он из себя представляет?
На какие две группы разделяют многоугольники? Опишите выпуклый многоугольник.
Выберете из данных многоугольников выпуклые 
1. 2. 
3.  4. 4. 
 
5 6.

 7. 8.
А остальные фигуры что из себя представляют? Теперь поговорим об объемных телах. Проводя аналогию, на какие 2 группы можно разделить эти фигуры? Попробуйте по аналогии с многоугольником описать, что это за фигура – многогранник. Далее учитель показывает фигуру, напоминающую открытую коробку и спрашивает. Эта фигура будет многогранником? Поэтому необходимо выполнение ещё одного условия, чтобы фигура была многогранником, как вы думаете, какого?
Сформулируйте теперь определение многогранника.
А какие многогранники вы знаете? А зачем нам нужно изучать многогранники? Оглянитесь вокруг, многогранники окружают нас всюду. Многие здания имеют форму многогранников (здесь можно учащимся показать картинки). Когда вы приходите домой из школы, то вешаете свои вещи в шкаф, а шкаф это тоже многогранник; мел, которым мы пишем, также многогранник. Таких примеров может быть очень много. По аналогии с многоугольниками, на какие 2 класса можно разбить многогранники? Попробуйте описать выпуклый многогранник, учитывая, что аналогом прямой в пространстве будет плоскость. А какие вы знаете выпуклые многогранники? (В результате появляется таблица)
 Геометрические фигуры Геометрические фигуры
  Плоские
Многоугольник Немногоугольники  
Выпуклые Невыпуклые
Итак, мы проклассифицировали все геометрические фигуры. Тем самым повторили изученные ранее многоугольники и сделали первые шаги к изучению многогранников. Данная схема поможет вам на основе аналогии с многоугольниками ввести корректное определение многогранника, его составляющих элементов, свойства и их обоснование. А почему именно на основе аналогии? Да потому что аналогами многоугольников в пространстве являются многогранники. Попытайтесь теперь сформулировать цель нашего урока. Сегодня на уроке мы также рассмотрим некоторые виды многогранников и их составляющие элементы. Запишите тему урока: «Многогранники. Призма. Пирамида». Поскольку аналогом многоугольника в пространстве является многогранник, то прежде чем рассматривать новую фигуру и её элементы, повторим составляющие элементы многоугольника. Перед вами канва-таблица. Левая колонка называется многоугольник и соответственно изображён многоугольник ABCDE, правая колонка – многогранник и изображён многогранник ABCDA1B1C1D1. Перечислите, из каких элементов состоит многоугольник? Перечислите вершины многоугольника ABCDE. Стороны? Диагонали? (Всё заносим в канву – таблицу). Теперь перейдём к рассмотрению многогранника. При изучении тетраэдра и параллелепипеда как мы называли треугольники и параллелограммы, из которых состоят эти фигуры? А как называли стороны этих граней? Их вершины?
Какой ещё элемент параллелепипеда вы не назвали? Что называют диагональю параллелепипеда? Попробуйте обобщить сказанное вами на случай многогранника. Какие получим составляющие элементы многогранника? Перечислите грани многогранника ABCDA1B1C1D1. Рёбра
Вершины. Назовите 2 любые диагонали граней многогранника. Назовите диагонали многогранника. Сформулируйте определение граней многогранника? Рёбер многогранника?
Вершин многогранника?
Что называется диагональю многогранника?
Назовите многоугольник с наименьшим количеством диагоналей? Или одним словом четырёхугольник. Назовите многогранник с наименьшим количеством диагоналей? Перечислите углы рассматриваемого многоугольника. Какие они по виду? А какие ещё бывают углы? А трёхгранные углы бывают? Действительно, и трёхгранные углы бывают и четырёхгранные и многогранные. Как вы думаете, какие углы могут быть у многогранника? Приведите примеры плоского угла на рассматриваемом многограннике. Приведите примеры двугранных углов. В рассматриваемом многраннике ABCDA1B1C1D1 есть и трёхгранные углы. Например, трёхгранный угол при вершине А, поскольку данный угол ограничивают 3 грани: ABCD, ABB1A1, и AA1D1D. Приведите пример трёхгранного угла в классе? Когда изучали многоугольники, то вам приходилось находить сумму углов. По какой формуле вы это делали? Как вы думаете, можно посчитать сумму углов у многогранника? Действительно можно, но только у выпуклого многогранника. А сумму каких углов можно подсчитать у многогранника?
Верно. А сделать это можно следующим образом: рассмотрим некоторую фигуру – четырёхугольную пирамиду. Я надрежу эту пирамиду вдоль рёбер, а вершину оставлю. Посмотрим, как выглядит развёртка четырёхгранного угла на плоскости. Обозначим углы граней при вершине У1, У2, У3, У4. Точно мы не сможем подсчитать сумму этих углов, но можем сказать определённо, в каких границах она находится. Итак, У1+У2+У3+У4 однозначно больше 00 , но меньше скольки градусов? На самом деле, у выпуклых многогранников есть такое свойство, что сумма плоских углов при каждой его вершине меньше 3600. Т.е. У1+У2+У3+У4 0. Ещё какими величинами можно охарактеризовать многоугольник. Как найти периметр многоугольника? Аналогично у многогранника можно посчитать сумму длин всех рёбер. Как найти площадь многоугольника ABCDE? Аналогично у многогранника можно найти площадь боковой поверхности как сумму площадей боковых граней многогранника. И площадь полной поверхности как сумму площади боковой поверхности и площади основания. У многогранников ещё можно находить объём, поскольку это объёмные фигуры. Об объёме и формулах объёма для многогранников поговорим позднее. А теперь перейдём к рассмотрению конкретных видов многогранников и прежде всего рассмотрим призму.(Учитель показывает учащимся натуральные модели призм). С этой фигурой мы ещё с вами не встречались, но сегодня на уроке мы должны познакомиться с призмой и рассмотреть её основные элементы. Призма. Пусть заданы две параллельные плоскости  и β. Рассмотрим два равных многоугольника А1А2…Аn, В1В2…Bn, расположенные в этих плоскостях. Соединим соответственные вершины многоугольников параллельными отрезками А1В1, А2В2, …, АnBn. (смотри канву-таблицу). и β. Рассмотрим два равных многоугольника А1А2…Аn, В1В2…Bn, расположенные в этих плоскостях. Соединим соответственные вершины многоугольников параллельными отрезками А1В1, А2В2, …, АnBn. (смотри канву-таблицу). Какой плоской фигурой будет каждый из полученных n-четырёхугольников A1А2В2В2, A2А3В3В2,…, AnА1В1Вn ? Это лишь гипотеза, её необходимо объяснить. Какой четырёхугольник мы называем параллелограммом?
Пользуясь определением, докажем, что четырёхугольник А1В1 В2А2 параллелограмм. Что вы можете сказать об отрезках A1В1 и A2В2? Откуда это следует? А отрезки A1А2 и В1В2. Какие они? Почему? Что известно про плоскости  и β? И по сути мы видим, что они пересечены третьей плоскостью А1В1 В2А2 . и β? И по сути мы видим, что они пересечены третьей плоскостью А1В1 В2А2 . Тогда откуда следует параллельность отрезков В1В2 и A1А2?
Давайте вспомним это свойство.
Таким образом, мы получили, что в четырёхугольнике А1В1В2А2 противоположные стороны попарнопараллельны, а значит доказали, что четырехугольник А1В1В2А2 – параллелограмм. Аналогично можно доказать, что и другие четырёхугольники также будут параллелограммами. Введём определение призмы. Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенные в параллельных плоскостях, и n-параллелограммов A1А2В2В1 ,…, AnА1В1Вn называется призмой. Заметим, что параллелограммов столько, сколько вершин у многоугольников. Вершин n и параллелограммов также n. (Дальше учитель берёт натуральные модели тетраэдра и параллелепипеда, показывает на грань, лежащую в основании). Как мы называли эту грань? Проводя аналогию с тетраэдром и параллелепипедом, как назовём многоугольники А1А2 … Аn , В1В2…Bn? Параллелограммы, из которых составлена призма?
Отрезки A1В1, A2В2, …, AnВn ?
(Всё заносим в канву-таблицу). Что можно сказать о боковых рёбрах призмы? (учитель показывает натуральную модель призмы) Откуда это следует?
Призму с основаниями А1А2 … Аn, В1В2…Вn обозначают А1А2 … АnВ1В2…Вn и называют n-угольной призмой. Любой выпуклый многогранник имеет высоту. Введём определение высоты призмы. Высота призмы – это перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания. (смотрим канву-таблицу и просим учащихся построить там высоту призмы). Проведём в призме ещё несколько высот. Поскольку высота призмы – это перпендикуляр, проведённый из любой точки одного основания к плоскости другого основания, то в качестве такой точки возьмём, например, одну из вершин верхнего основания призмы точку D1 и опустим из неё перпендикуляр на плоскость нижнего основания. В этом случае, где оказалась проекция высоты призмы? Теперь возьмём точку С1 и опустим из неё перпендикуляр на плоскость основания. В этом случае где оказалась проекция высоты призмы? Далее учитель показывает учащимся натуральные модели прямой и наклонной призм. Чем отличаются эти 2 призмы?
Такую призму, у которой боковое ребро перпендикулярно к основаниям называют прямой. Приведите примеры прямых призм, с которыми мы не раз встречались на уроках геометрии. (Учитель показывает натуральную модель прямой призмы). На натуральной модели прямой призмы возьмём любое боковое ребро. Мысленно пытаемся провести высоту призмы. Сравните боковое ребро и высоту прямой призмы. Это выполняется только для прямой призмы. Если призма не является прямой, то её называют наклонной. Попробуйте, исходя из определения прямой призмы, сформулировать определение наклонной призмы.
Та призма, которая у вас в канве-таблице наклонная или прямая? (далее учитель показывает натуральные модели правильных призм, например, правильной треугольной призмы и куба). Это модели правильных призм. Как вы думаете, что должно быть, чтобы призма была правильной? Что лежит в её основании? Какое ещё условие должно выполняться, чтобы призма была правильной? Посмотрите на натуральные модели правильной призм, эти призмы прямые или наклонные? Таким образом, прямая призма называется правильной, если её основания правильные многоугольники. Обращаю внимание на то, что только прямая призма может быть правильной. Давайте посмотрим на модели правильных призм, что вы можете сказать об их боковых гранях? Сравните их. Какой плоской фигурой будут боковые грани правильной призмы? Таким образом, правильная призма обладает следующим свойством: все её боковые грани – равные прямоугольники. (заносим её в канву-таблицу) Это свойство необходимо доказать. На доске изображена правильная призма, проводим доказательство, пользуясь этим рисунком и натуральной моделью. Сначала докажем, почему боковые грани правильной призмы прямоугольники. Какую призму мы можем назвать правильной?
Что известно про прямую призму?
А теперь объясните, почему эти прямоугольники равные? Чем характеризуется прямоугольник? Рассмотрим два соседних прямоугольника и докажем, что они равны. Что нужно сравнить у этих прямоугольников?
Таким образом, мы доказали, что в правильной призме все боковые грани – равные прямоугольники. Когда мы изучали выпуклые многоугольники, то мы решали задачи о нахождении их площади. У многогранников также можно находить площадь как боковой поверхности, также и полной поверхности. Как вы думаете, что называют площадью боковой поверхности призмы?
А что такое площадь полной поверхности призмы? Площадь полной поверхности выражается через площадь боковой поверхности и площадь основания призмы формулой. Как вы думаете какой? Посмотрим на прямую призму, изображённую на доске. И поставим перед собой задачу: найти площадь её боковой поверхности. Какой плоской фигурой будут боковые грани прямой призмы?
Основания этих прямоугольников по отношению к призме чем являются? Сравните высоты этих прямоугольников и высоту призмы. (рисунок в канве-таблице) Как найти площадь боковой поверхности прямой призмы?
Вспомним формулу площади прямоугольника. Распишем теперь площади прямоугольников  и полученные результаты подставим в формулу площади боковой поверхности прямой призмы, учтем, что AA1=BB1=…=FF1=h. и полученные результаты подставим в формулу площади боковой поверхности прямой призмы, учтем, что AA1=BB1=…=FF1=h. Сумма длин всех сторон основания, это что? Таким образом, мы доказали теорему о нахождении площади боковой поверхности прямой призмы. А теперь попробуйте сформулировать сами данную теорему.
Заметим, что эта теорема верна лишь для прямой призмы. В канву-таблицу запишем план доказательства, а само доказательство предлагаю восстановить дома. Помимо прямой призмы есть ещё и наклонная. Как же находить площадь её боковой поверхности? Для этого решим задачу №236. Читаем задачу и делаем рисунок. Что такое перпендикулярное сечение наклонной призмы?
Строим перпендикулярное сечение наклонной призмы (смотри канву-таблицу и рисунок на доске)

Проводим высоту h1 грани AA1B1B обозначим ММ1. затем из точки М1 опустим перпендикуляр на ребро СС1, получим точку М2, затем из точки М2 опустим перпендикуляр на ребро DD1 и так далее во всех гранях проводим высоты h1, h2,…, hn. В результате получим перпендикулярное сечение ММ1М2…Мn. Обозначим за 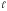 боковое ребро наклонной призмы. боковое ребро наклонной призмы. Какой плоской фигурой является боковая грань наклонной призмы? Вспомним формулу площади параллелограмма.
Найдите площадь каждой боковой грани наклонной призмы, обозначив боковое ребро за 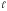 . . Найдите теперь площадь боковой поверхности наклонной призмы. h1, h2,…, hn – это что для сечения? Чему равна сумма длин отрезков h1, h2,…, hn ?
Таким образом мы доказали, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на высоту. Запишем план доказательства, а само доказательство вы восстановите дома. Пирамида. Рассмотрим ещё один многогранник – пирамиду. (Учитель показывает натуральную модель). Рассмотрим многоугольник А1А2 … Аn и точку Р, не лежащую в плоскости этого многоугольника. Соединим точку Р отрезками с вершинами многоугольника, получим n-треугольников. (Смотри канву-таблицу). Назовите их. Попытайтесь по аналогии с определением призмы сами сформулировать определение пирамиды.
По аналогии с определениями, введёнными для призмы, дайте определение основных элементов пирамиды: основание, боковые грани, боковые рёбра, вершина пирамиды. По аналогии с определением n-угольной призмы дайте определение n-угольной пирамиды. (всё заносится в канву-таблицу). Попытайтесь сформулировать определение высоты пирамиды.
Постройте высоту пирамиды, которая дана у вас в канве-таблице. Проекция точки Р лежит в плоскости основания в этом случае. Далее учитель показывает натуральные модели пирамид;1) проекция высоты пирамиды лежит вне плоскости основания. 2)проекция высоты пирамиды лежит на ребре основания в случае, когда боковая грань перпендикулярна основанию. 3)высота призмы совпадает с боковыми рёбрами в случае, когда боковое ребро перпендикулярно основанию.
По аналогии с определениями площади полной и боковой поверхности призмы сформулируйте определение площади полной и боковой поверхности пирамиды. Запишите формулу площади полной поверхности пирамиды через площадь боковой поверхности и площадь основания. Поскольку призма бывает правильной, то очевидно можно предположить, что есть и правильная пирамида, но понятия прямой пирамиды в геометрии, вообще говоря, нет. Попробуйте по аналогии с определением правильной призмы сформулировать определение правильной пирамиды, учитывая, что нет понятий прямой пирамиды. Поскольку в определении правильной призмы учитывалось выполнение двух условий, то в этом определении также должны выполняться 2 условия и второе условие такое: отрезок, соединяющий вершину пирамиды с центром основания, является её высотой. Вспомним что такое центр правильного многоугольника? Пользуясь натуральной моделью и рисунком правильной пирамиды из канвы-таблицы, что вы можете сказать о её боковых рёбрах и боковых гранях. Сравните боковые грани, они между собой какие? Действительно, правильная пирамида обладает следующим свойством: все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. Запишите это свойство в канву-таблицу Докажем это. Сначала докажем, что все боковые рёбра этой пирамиды равны. Проведём в пирамиде высоту РО, проводим её и в канве-таблице. Соединим центр основания пирамиды с вершинами пирамиды. На какие плоские фигуры разбилась пирамида? Чем являются боковые рёбра пирамиды для этих треугольников? Рассмотрим 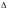 А1РО (смотри канву-таблицу). А1РО (смотри канву-таблицу). ОР для пирамиды, чем является? Обозначим ОР за h(ОР=h). АО1 чем является для этой пирамиды?
Как найти гипотенузу А1Р? Полученные прямоуголные треугольники между собой какие? Сравните их. По какому признаку они равны? Что можно сказать о гипотенузах этих треугольников?
При доказательстве этого факта, какой метод мы использовали? Докажем теперь, что боковые грани правильной пирамиды равные равнобедренные треугольники. Объясните, почему эти треугольники равнобедренные?
Осталось доказать, что равны их основания. Докажите это.
По какому признаку равны эти грани? Возьмём любую боковую грань правильной пирамиды и проведём в ней все высоты (в канве-таблице проводим эти высоты). Поскольку боковая грань правильной пирамиды – треугольник, то в ней можно провести три высоты. Одна из этих высот, а именно высота, проведённая из вершины пирамиды, имеет специальное название – апофема. Дайте определение апофемы правильной пирамиды.
Понятие апофемы нам нужно для того, чтобы сформулировать и доказать теорему о нахождении площади боковой поверхности правильной пирамиды. Поставим перед собой задачу: найти площадь боковой поверхности правильной пирамиды. Каким свойством обладают боковые грани правильной пирамиды? Чему равна площадь такого треугольника, если апофему обозначить за d? Давайте распишем площади этих треугольников.
Основания этих треугольников, чем являются по отношению к пирамиде? Чему по определению равна площадь боковой поверхности пирамиды?
Таким образом, мы доказали теорему о площадь боковой поверхности правильной пирамиды. Сформулируйте её.
Запишем план доказательства (смотри канву-таблицу), а доказательство вы восстановите дома. Существует ещё особый вид пирамиды – усечённая пирамида. ( учитель показывает натуральную модель). Её я вам предлагаю изучить самостоятельно дома по тому же плану, по которому мы рассматривали призму и пирамиду. (план записывается учителем на доске).
Познакомившись с данными видами многогранников, давайте спрогнозируем нашу дальнейшую деятельность. Чтобы усвоить новый материал и новые понятия необходимо решить ряд задач. Этим мы займёмся на последующих уроках. Давайте ещё раз вспомним, с какими новыми понятиями мы сегодня познакомились?
Какие теоремы доказали на уроке?
Что помогло нам «открыть» определения некоторых понятий?
Д/з: п. 25-29 читать, восстановить доказательства теорем по планам. п. 30-самостоятельно изучить по предложенному плану. |
Деятельность ученика
На плоские и объёмные.
Многоугольники и немногоугольники.
Фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек, называется многоугольником.
На выпуклые и невыпуклые. Выпуклый многоугольник лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Выпуклые многоугольники изображены под номерами: 1, 3, 5, 6, 7.
Невыпуклые многоугольники.
Объёмные геометрические фигуры можно разделить на многогранники и немногогранники.
Поверхность, составленная из многоугольников, называется многогранником.
Нет
Поверхность должна ограничивать некоторое геометрическое тело. Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником. Тетраэдр, параллелепипед.
На выпуклые и невыпуклые. Выпуклый многогранник находится по одну сторону от плоскости каждой его грани.
Тетраэдр, параллелепипед

  Объёмные Объёмные
Многогранники Немногогранники  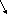
Выпуклые Невыпуклые
На основе аналогии с многоугольником ввести понятие многогранника.
Многоугольник состоит из вершин, сторон, диагоналей, углов.
A, B, C, D, E. EA, AB, BC, CD. AC, EC, EB, BD, AD.
Гранями.
Рёбрами. Вершинами параллелепипеда или тетраэдра.
Диагональ.
Отрезок, соединяющий противоположные вершины.
Вершины, рёбра, грани, диагонали.
ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D, AA1D1D. AA1, BB1, CC1, DD1, AB, BC, CD, AD, A1B1, B1C1, C1D1, A1D1. A, B, C, D, A1, B1, C1, D1. BD, AB1.
A1C, C1A, B1D, D1B.
Многоугольники, из которых составлен многогранник, называются его гранями. Стороны граней называются рёбрами многогранника. Концы рёбер называются вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Трапеция, прямоугольник, квадрат.
Параллепипед, куб.
 В, В,  А, А,  С, С,  D, D,  Е. Е.
Плоские Двугранные Да
Плоские, двугранные, трёхгранные, многогранные.
 BAD, BAD,  BAA1, BAA1,  C1D1D, … C1D1D, …
D1ADC, B1ABC …
Две стены и пол, две стены и потолок.
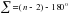 , где n-количество рёбер. , где n-количество рёбер.
Наверное, можно.
При какой-нибудь вершине, сумму плоских углов.

3600.
Периметром, площадью.
Нужно найти сумму длин всех сторон
SABCDE=SCBE+SCAE+SCED

Каждый из полученных n-четырёхугольников является параллелограммом.
Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
Они параллельны. Из построения призмы.
Параллельные.
Они параллельны
Из свойства параллельности двух плоскостей, пересечённых третьей плоскостью. Если 2 параллельные плоскости пересечены третьей, то линии пересечения этих плоскостей параллельны.
Основанием.
Основаниями призмы.
Боковые грани призмы.
Боковыми рёбрами призмы.
Они равны и параллельны.
Это следует из того, что боковые грани - параллелограммы, а в параллелограмме противоположные стороны равны и параллельны.
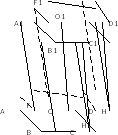
Вне основания призмы.
На ребре нижнего основания.
У одной из них боковое ребро перпендикулярно к основанию призмы.
Куб, параллелепипед.
Высота прямой призмы равна её боковому ребру.
Если боковое ребро призмы не перпендикулярно к основаниям, то призма называется наклонной.
Наклонная, так как её боковое ребро не перпендикулярно к основаниям.
Правильный многоугольник.
Прямые
Они равны.
Прямоугольниками. 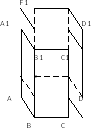
Прямую призму, у которой основания правильные многоугольники.
Её боковое ребро перпендикулярно к основаниям, а значит боковые грани правильной призмы – прямоугольники.
Длиной и шириной.
Длину и ширину. А1В1 = АВ = В1С1 = ВС, т.к. АВСD…F, A1B1C1D1 …F1 – равные правильные многоугольники, А1А = ВВ1 = СС1 как боковые рёбра призмы.
Площадью боковой поверхности называют сумму площадей её боковых граней. Площадью полной поверхности призмы называется сумма площадей всех её граней.
Sпол=Sбок+2Sосн.
Боковые грани прямой призмы – прямоугольники.
Сторонами основания призмы.
Высоты прямоугольников равны высоте призмы. AA1=BB1=…=FF1=h. Найти сумму площадей её боковых граней (прямоугольников). 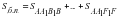 Площадь прямоугольника равна произведению его смежных сторон.
Sб.п.=AA1*АB+ВВ1*ВС+…+AA1*АF=h*АВ++h*ВС+…+h*АF=h(АВ+ВС+…+АF)=h*P
Периметр.
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Перпендикулярным сечением наклонной призмы называется её сечение плоскостью, перпендикулярной к боковым рёбрам и пересекающей их.
Параллелограммом. Площадь параллелограмма равна произведению высоты параллелограмма на его основание.
S1=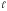 *h1 *h1 S2=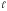 *h2 *h2 S3=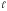 *h3 *h3
Sб.п.= 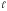 *h1+ *h1+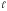 *h2+…+hn= *h2+…+hn=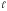 (h1+h2+…+hn) (h1+h2+…+hn) Стороны сечения.
Периметру перпендикулярного сечения. Sб.п.=  *P. *P.

РА1А2, РА2А3,…, РАnА1.
Многогранник, составленный из n-угольника А1А2 … Аn и n-треугольников РА1А2, РА2А3,…, РАnА1 называется пирамидой. Многоугольник А1А2 … Аn называется основанием пирамиды, треугольники РА1А2, РА2А3,…, РАnА1 – боковыми гранями. Точка Р – вершиной пирамиды. Отрезки РА1, РА1,…, РАn – боковыми рёбрами пирамиды
Пирамиду с основаниями РА1А2 …Аn и вершиной Р обозначают РА1А2…Аn и называют n-угольной пирамидой.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания называется высотой пирамиды.
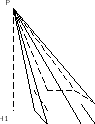
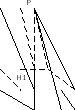
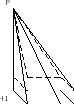 Площадью полной поверхности пирамиды называется сумма площадей всех её граней, а площадью боковой поверхности пирамиды – сумма площадей её боковых граней.
Sп.п.=Sбок.+Sосн.
Пирамида называется правильной, если её основание – правильный многоугольник.
Центр вписанной в него (или описанной около него) окружности.
Боковые рёбра правильной пирамиды равны, а боковые грани – равнобедренные треугольники.
Равные.
На прямоугольные треугольники.
Гипотенузами.
Высотой.
АO1=R, R-радиус описанной окружности. По теореме Пифагора А1Р=
Равные.
По двум катетам.
Они также равны. РА1=РА2=…=РАn= . .
Метод равных треугольников.
Мы только что доказали, что боковые рёбра правильной пирамиды равны, а значит её грани равнобедренные треугольники.
Основания этих треугольников равны друг другу, так как А1А2 … Аn - правильный многоугольник. Значит боковые грани равные и равнобедренные треугольники.
По 3 – ему признаку равенства треугольников.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
Боковые грани правильной пирамиды равные равнобедренные треугольники.
Половине произведения апофемы на основание треугольника. SA1PA2=1/2d*A1A2 SA2PA3=1/2d*A2A3 SA1PAn=1/2d*A1An
Сторонами основания пирамиды.
Сумме площадей всех её граней. S=S1+S2+…+Sn=1/2d*A1A2 +1/2d*A2A3 + +1/2d*A1An =1/2d(A1A2 + A2A3 +… + A1An )=1/2d*P.
Теорема: площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
План: графическая модель (рисунок) определение усечённой пирамиды. Элементы усечённой пирамиды Свойство боковых граней усечённой пирамиды с доказательством. Правильная усечённая пирамида. Площадь боковой поверхности правильной усечённой пирамиды (с доказательством).
Пирамида, призма, многогранник, основные элементы многогранников, прямая и правильная призма, правильная пирамида. Свойство боковых граней прямой призмы, теорему о нахождении площади боковой поверхности прямой и наклонной призмы, свойство правильной пирамиды, теорему о нахождении боковой поверхности правильной пирамиды
Аналогия в формулировках определений, теорем.
|


 4.
4. 




 Геометрические фигуры
Геометрические фигуры
 и β. Рассмотрим два равных многоугольника А1А2…Аn, В1В2…Bn, расположенные в этих плоскостях. Соединим соответственные вершины многоугольников параллельными отрезками А1В1, А2В2, …, АnBn. (смотри канву-таблицу).
и β. Рассмотрим два равных многоугольника А1А2…Аn, В1В2…Bn, расположенные в этих плоскостях. Соединим соответственные вершины многоугольников параллельными отрезками А1В1, А2В2, …, АnBn. (смотри канву-таблицу). и полученные результаты подставим в формулу площади боковой поверхности прямой призмы, учтем, что AA1=BB1=…=FF1=h.
и полученные результаты подставим в формулу площади боковой поверхности прямой призмы, учтем, что AA1=BB1=…=FF1=h.
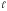 боковое ребро наклонной призмы.
боковое ребро наклонной призмы.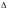 А1РО (смотри канву-таблицу).
А1РО (смотри канву-таблицу).
 В,
В, 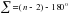 , где n-количество рёбер.
, где n-количество рёбер.