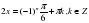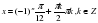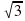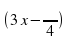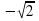Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
на тему
«Решение уравнений вида sinx=a».
Выполнил:
преподаватель математики
первой квалификационной категории
Заварзина В.Г.
Липецк 2015 г.
Тема урока:
” Решение уравнений вида sinx = a. “
Цели урока:
1. Образовательные:
а) Повторить с учащимися определение и свойства функции у = sinx и ее график.
б) Закрепить навыки решения простейших тригонометрические уравнений, а также уравнении, сводящихся к простейшим в результате преобразования тригонометрических выражений.
2. Развивающие:
а) развитие профессиональных качеств обучающихся (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а) воспитание навыков самостоятельной работы;
б) воспитание дисциплинированности;
в) воспитание эстетических взглядов.
Тип урока: повторение
Методические приемы: -практический- решение задач
Межпредметные связи: химия-физика- производственное обучение.
Оборудование и наглядные средства обучения: мультимедийный проектор, интерактивная доска, презентация, задачник “Алгебра и начала математического анализа” (профильный уровень часть 1) под редакцией А. Г. Мордковича .
Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока.
Организационный момент:
Подготовка учащихся к уроку (проверка отсутствующих на уроке, наличие тетрадей)
Сообщение темы и целей урока.(слайд 1,2)
Эпиграф к уроку : ”Изучать что-либо и не задумываться над выученным - абсолютно бесполезно.
Задумываться над чем-либо, не изучив
предварительно предмет раздумий-
опасно.” Конфуций.(слайд 3)
В наших домах, в транспорте, на заводах - всюду работает электрический ток.
Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
Тригонометрические уравнения имеют применение во многих науках: химии, физики, биологии….
Этот урок- первый шаг к изучению тригонометрических уравнений.
2. Проверить домашнее задание по вопросам.(даны подробные ответы)
 a) Дайте определение функции sinx.
a) Дайте определение функции sinx. Q(a; b)

 Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки).
Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки). Рис.1
х
Пусть конец единичного радиуса OQ, соответствующего углу х,
совпадает с точкой Q(a;b) окружности; тогда координаты (a;b) точки Q называют координатами конца радиуса, соответствующего углу х.
Определение. Число, равное ординате конца единичного радиуса, соответствующего углу х, называется синусом угла х и обозначается sinx.
Поскольку каждому значению величины угла х на тригонометрическом круге соответствует единственная точка Q(a;b) такая, что радиус OQ образует угол х с осью абсцисс, то введенное отображение y = sinx является функцией.
б) Какая область определения функции?
Область определения функции y = sinx – множество действительных чисел. Пишут D(sin) = R.
в)Какая область значений функции?
E(sin) = [-1;1]. Значение ординаты b будет синусом угла, образованного положительным направлением оси абсцисс и радиусом, соединяющим центр окружности и построенную точку.
г) Назовите периодичность функции.
Наименьший положительный период функции равен 2π . Докажем, что это наименьший положительный период. Рассмотрим значение функции y = sinx, равное единице. Оно достигается, только если х = π/2 + 2πn, n є Ζ. Следовательно, никакое число, меньшее 2π не может быть периодом.



 д) Что мы имеем: четность или нечетность?
д) Что мы имеем: четность или нечетность? M(a,b)
Рассмотрим (рис.2) точки M и N, соответствующие на тригонометрическом круге углам х и –х. Поскольку всякий круг симметричен относительно любой прямой, проходящей через его центр (а ось Оx является такой прямой), и равные по величине углы при симметрии переходят в равные углы, то точки M и N симметричны относительно оси Оx, следовательно, их ординаты противоположны. Это означает, что для любого значения х выполнено
sin(-x) = -sinx, т. е. функция y = sinx является нечетной.
е) Какие точки пересечения графика с осями координат? N(a;-b)
График пересекает ось Ох в точках с абсциссами, определяемыми уравнением sinx=0, т. е. Рис.2
х = πn, n є Ζ; график пересекает ось Оу в точке с ординатой,
определяемой равенством y = sin0, т.е. у = 0.
ж) Назовите промежутки знакопостоянства функции.
Так как ординаты точек, лежащих в верхней полуплоскости, положительны, а точек, расположенных в нижней полуплоскости, отрицательны, то sinx 0 при
х є (2πk; π + 2πk), k є Ζ; sin x
з) Назовите наибольшее и наименьшее значение.
Наибольшее значение, равное 1, достигается при х = π/2 + 2πn, n є Ζ ; наименьшее значение, равное -1, достигается при х = - π/2 + 2πn, n є Ζ ;
и) Назовите интервалы возрастания и убывания.
Функция не является монотонной на всей области определения; она является монотонной на отрезках: возрастает при х є ( - π /2 +2πk; π /2 + 2πk), k є Ζ; убывает при
х є (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ .
к) Есть ли асимптоты. График функции асимптот не имеет.
3. Повторение.
Решение уравнения sin х = а.
Поскольку по определению синусом угла называется ордината точки, лежащей на окружности единичного радиуса, то для решения уравнения
sin x =a надо найти на окружности все точки имеющие ординату a, т.е. лежащие на прямой y = a. По теореме о взаимном расположении прямой и окружности на плоскости заключаем, что при |a| 1 прямая и окружность общих точек не имеют, следовательно и рассматриваемое уравнение не имеет решений. Если |a| = 1, то прямая y = a касается окружности, т.е. имеет с ней ровно одну общую точку C. Наконец, если |a| sin x = a вводят понятие арксинуса числа a. Чтобы однозначно определить угол, соответствующий числу а, приходится требовать выполнения дополнительного условия, например, чтобы этот угол принадлежал интервалу [-π /2; π /2].
Определение. Арксинусом числа а, а є [-1;1], называется такое число х, принадлежащее отрезку [-π /2; π /2], синус которого равен а. Это число обозначается arcsin a.
Учитывая периодичность функции y = sin x, получим серию решений
x = arcsin a + 2πk, k є Ζ .
Точка В, как отмечалось, симметрична точке А относительно оси Оу, поэтому ей соответствует угол х2 = π − arcsin a, поэтому можно записать вторую серию решений
x = π − arcsin a + 2πk, k є Ζ .
Других решений рассматриваемое уравнение иметь не может, поскольку противное означало бы, что окружность и прямая пересекаются более чем в двух точках.
Для сокращения записи две полученные серии решений обычно объединяют в одну
x = (-1)  arcsin a + πk, k є Ζ .
arcsin a + πk, k є Ζ .
При четных значениях k эта формула соответствует первой серии решений; при нечетных — второй.
4. Решение нескольких примеров на доске.(слайд 4)
Пример 1
Решить уравнение:
Sin x =- 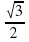
Применяя формулу получим:
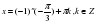
Знак минус можно внести в степень. Тогда получится следующая формула:
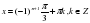
Ответ:
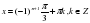
Пример 2
Решить уравнение:
Sin x - 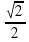 =0
=0
Приведем уравнение к простому виду.
Sin x = 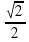
Применяя фомулу получим:
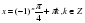
Ответ:
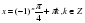
Пример 3
Решить уравнение:
Sin2x -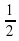 =0
=0
Приведем уравнение к виду:
Sin2x =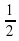
Применяя фомулу получим:
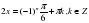
Разделим все уравнение на 2.
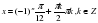
Ответ: 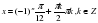
Пример 4
Решить уравнение:
Sin2x= 5
Данное уравнение решений не имеет.
Ответ: решений нет.
Пример 5.
Решить уравнение sin(π /6 – 2x) = √3 /2.
Имеем π /6 – 2x = ( - 1)  arcsin √3 /2 + πk.
arcsin √3 /2 + πk.
Так как arcsin √3 /2 = π /3,
то
π /6 – 2x = ( - 1)  π /3 + πk,
π /3 + πk,
откуда х = - ( - 1)  π /6 + π /12 + πk /2,
π /6 + π /12 + πk /2,
или
х = (-1)  π /6 + π /12 (6k + 1), k є Ζ.
π /6 + π /12 (6k + 1), k є Ζ.
Пример 6. Решить уравнение (1-sinx)(tg  x-3) = 0.
x-3) = 0.
Найдем значения х, удовлетворяющие каждому из уравнений 1-sinx = 0 и tg  x-3 = 0; если sinx = 1,то получим
x-3 = 0; если sinx = 1,то получим
x = π /2 + 2πk, k є Ζ; (1)
если tg x = 3, т. е. tgx = ±√3, то
x = 3, т. е. tgx = ±√3, то
x = ±π /3 + πn, n є Ζ. (2)
Однако было бы ошибочным считать ответом объединение решений (1) и (2).
Ответом является только второе решение x = ±π /3 + πn, n є Ζ.
Пример 7
sinx = 0,3
Решение: х = (-1)narcsin 0,3 + πn, n ∈ Z
Самостоятельная работа.(слайд 5)
I Вариант.
Sin x = 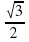
Sin 2x = 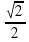
Sin x = 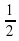
2Sin  =
=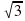
II Вариант.
Sin x = 1
Sin x =- 1 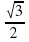
Sin =-2
=-2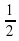
2Sin 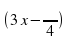 =
=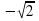
(Обучающиеся делают работу на листочках и сдают на проверку)_
Заключение урока.
Итог урока. Рефлексия. Оценки за урок. Вы сегодня решали тригонометрические уравнения. Что это за уравнения? Какой вид тригонометрических уравнений вы изучили?
Объявление отметок.
6. Домашнее задание из задачника № 22.8 (а,б)
Спасибо за урок!
Список литературы:
1. Дидактические материалы по алгебре и началам анализа для 10 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.
4. Алгебра и начала анализа: Учеб. для 10 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2003.
5. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
6. Галицкий М.Л. и др. Сборник задач по алгебре для 8-9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики/ М.Л. Галицкий, А.М.Гольдман, Л.И.Звавич. – 3-е изд. – М.: 1996. – 271 с.: ил.

 a) Дайте определение функции sinx.
a) Дайте определение функции sinx.
 Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки).
Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки).


 д) Что мы имеем: четность или нечетность?
д) Что мы имеем: четность или нечетность? 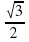
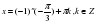
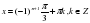
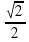 =0
=0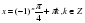
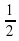 =0
=0