Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методическая разработка урока математики на тему «Решение линейных уравнений и неравенств»
I. Организационный этап
Подготовка учащихся к уроку (проверка отсутствующих на уроке, наличие тетрадей)
II. Актуализация опорных знаний учащихся
Сегодня, ребята, мы должны вспомнить всё, что мы знаем о линейных уравнениях, способах их решения. Вводится тема и цели урока. (слайд1,2)
Искусство решать уравнения и неравенства зародилось очень давно в связи с потребностями практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений и неравенств.
Устная работа с группой:
Преподаватель:
- Чтобы решить уравнение, нужно чётко понимать, чем вы занимаетесь, когда решаете уравнение.
-----
III. Решение примеров.
Используя свойства, решите следующие неравенства (работа в тетрадях и у доски):
1.
4 + 12х 7 + 13х;
Решение
Что бы решить данное неравенство необходимо перенести все известные числа в одну сторону, а неизвестное в другую.
12x-13x-4+7
-x3
Теперь поделим на -1
x 1;
Что бы решить данное неравенство необходимо сначала раскрыть скобки, а затем перенести все известные числа в одну сторону, а неизвестное в другую.
-2+3x+24+4x1
7x1+2-24
7x-21
Поделим неравенство на 7
x-3
Ответ: x
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение линейных уравнений и неравенств»
Просмотр содержимого презентации
«Презентация к уроку реш лин ур и нер»
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
1230 руб.
1760 руб.
1740 руб.
2480 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
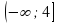 .
.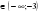
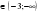
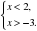
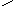










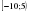 В.
В. 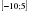
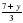 меньше дроби
меньше дроби 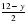 ?
?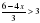
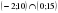 Б.
Б. 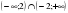 В.
В.