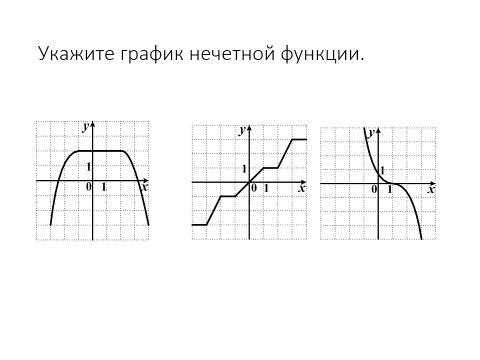
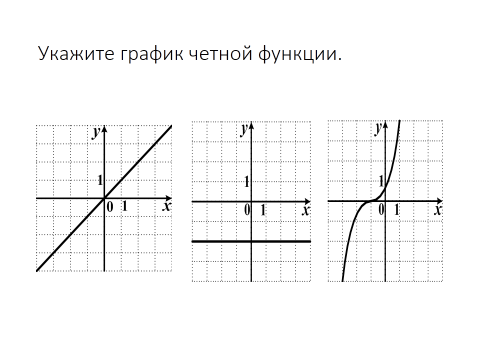
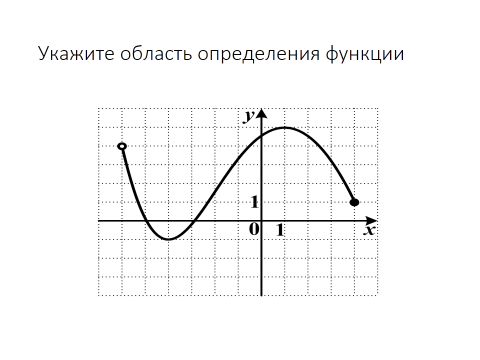
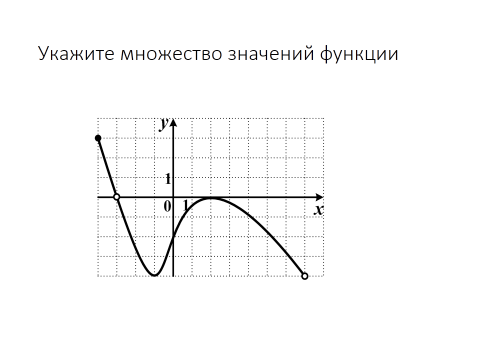
|
Фронтальная работа со всем классом. 5-7 мин
Объяснение новой темы 5-7 мин
Закрепление новой темы 3-4 мин
Практическая работа 4-5 мин
Самостоятельная работа нацеленная на закрепление первичных знаний Приложение №2
4-5 мин
Приложение №3
| Актуализация знаний учащихся Слово учителя о цели этого урока. Подготовка к изучению нового материала и постановка цели урока. Что такое область определения функции? Найти область определения для каждой из функций, y(1), y(-1), y(2), y(2) . У учащихся на парте карточки. | Функция | Область определения | y(1) | y(-1) | y(2) | y(-2) | | y (x) = 2x - 1 |
|
|
|
|
| | y(x) = x2 |
|
|
|
|
| | y(x) = x3 |
|
|
|
|
| | y(x) = 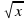 |
|
|
|
|
| | y(x) = 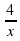 |
|
|
|
|
|
Проверка
| Функция | Область определения | y(1) | y(-1) | y(2) | y(-2) | | y (x) = 2 x - 1 | (-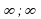 ) ) | 1 | -3 | 3 | -5 | | y(x) = x2 | (-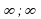 ) ) | 1 | 1 | 4 | 4 | | y (x) = x3 | (-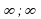 ) ) | 1 | -1 | 8 | -8 | | y(x) = 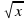 | 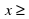 0 0
| 1 | - | 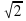
| - | | y(x) = 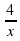 | x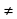 0 0 | 4 | -4 | 2 | -2 |
Создание проблемной ситуации
| Задания и вопросы учителя | Предполагаемые ответы учащихся | | 1. Сравните значения функции y=x2+1 при x=-3 и x=3 | Решение: y=x2+1 f(x)=x2+1 f(-3)= (-3)2+1=10 f(3)= 32+1=10 f(-3)=f(3)=10 | | Данная функция называется четной. Запишите определение четной функции. | Определение 1. Функцию у = f(х), х Є Х называют четной, если для любого значения х из множества Х выполняется равенство f(-x)=f(x).График четной функции симметричен относительно оси у. | | 2. Сравните значения функции y=x3-4x при x=5 и x=-5 | Решение: y=x3-4x f(x)=x3-4x f(-5)=(-5)3-4(-5)=-125+20=-105 f(5)=(5)3-4∙5=125+20=105 f(-5)=-f(5) | | Данная функция называется нечетной. Запишите определение нечетной функции.(слайд 11) | Определение 2. Функцию у = f(х), х Є Х называют нечетной, если для любого значения х из множества Х выполняется равенство f(- x )= -f (x).График нечетной функции симметричен относительно начала координат. | | Существуют функции, не являющиеся ни четными, ни нечетными. Пример: у=2х+3; у=х; у = (х-1)? | Учащиеся доказывают самостоятельно. | Исследуйте функцию на четность: f(x)=4x6-x2 Решение: f(x)=4(-x)6-(-x)2=4x6-x2 Вывод: f(x) четная функция. б) f(x)= x2-х+3 Решение: f(-x)= (-x2)-(-х)+3=x2+x+3=-(-x2-x-3) Вывод: функция ни четная, ни нечетная. Задания для самостоятельной работы Является ли чётной или нечётной функция: а) f(x) = x4- x2 ; б) f(x) = x3 – x; в) f(x) = 2x – 4 ? Построим совместно с учениками схему для определения четности функции. а) y(-x) = y(x) - четная; б) y(-x) = - y(x) - нечётная; в) Если хотя бы в одной точке из области определения y(-x) ≠ - y(x), то функция не является ни четной, ни нечетной. Пользуясь определением, выясним, какие из функций будут четными, а какие нечетными. № 172(1,3), 173(1,), № 175(1). Примеры четных и нечетных функций. y = |x|. Что можно сказать о графиках данных функций? Подведите учеников к тому, что при построении графиков четных функций используется осевая симметрия относительно оси ординат, а при построении графиков нечетных функций – центральная симметрия относительно точки начала координат (0;0). Вывод. А) График чётной функции симметричен относительно оси у. В) График нечётной функции симметричен относительно начала координат. №1. На рисунке изображены графики функций. Определите их четность.. 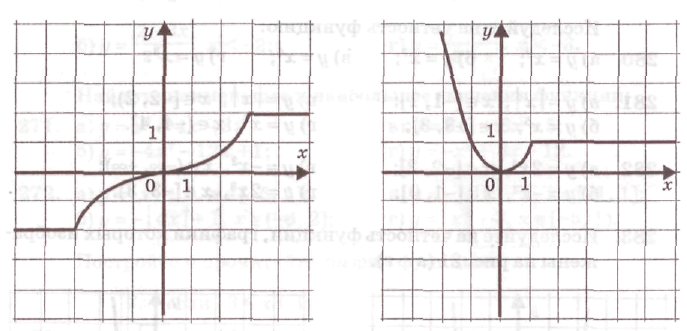 №2.На рисунке изображена часть графика чётной функции y = f(x). Изобразите весь график этой функции.
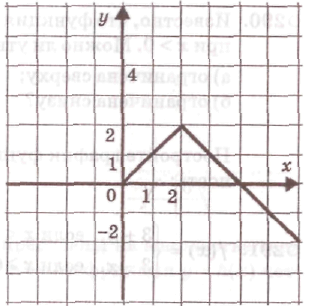 Заполните пропуски в формулировке определений и свойств:
1.Функция f(x) называется чётной, если область её определения симметрична относительно__________________________ и для любого значения аргумента х верно равенство f(-x) = __________ 2. Функция f(x) называется нечётной, если область её определения симметрична относительно__________________________ и для любого значения аргумента х верно равенство f(-x) = __________ 3. График любой чётной функции симметричен относительно__________________ 4. График любой нечётной функции симметричен относительно__________________
| 1. Учебник для учащихся 9 класса общеобразовательных учреждений под редакцией коллектива, авторов: Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова, «Алгебра 9 класс» Москва, «Просвещение», 2013г. 2. «Алгебра. Поурочные планы учебнику Ш.А. Алимова» Волгоград. «Просвещение», 2013г. Е.Г. Лебедев. 3. В.И. Жохов. «Дидактические материалы по алгебре. 9 класс».
ФО критерии успеха: знает и умеет определять четность, нечетность функции
ФО критерии успеха: умеет определять четность, нечетность функции
ФО критерии успеха: знает и умеет определять по графику функции четность, нечетность функции
ФО критерии успеха: знает определение четной, нечетной функции |
| Парная работа 9-10 мин
| Самостоятельная работа, на закрепление первичных знаний. Учащимся предлагается работа в парах. Им предоставляется список функции являющихся четными, нечётными или функциями общего вида. Паре дается задание произвести классификацию предложенных функций. По окончанию работы, предложите ученикам продемонстрировать свои выводы, причём один ученик доказывает нечётность выбранных функций, а другой – четность. Используйте список класса для того чтобы понять, кто смог верно прокомментировать свой выбор чётных (нечётных функций). Задание для учеников: Перед Вами список функций являющихся четными, нечётными или функциями общего вида, произведите классификацию предложенных функций 1.у = х4 - х3;
у = х3 + х4
у = х2 + х3;
4. у = х3 - х2
5. у = х3 - 5; 6. y = x4 - x2 ;
7. y = x3 – x;
8. y = 2x – 4
9.y = 4х3+7х
10.y =16х6 - 3х4
11. у= (х-2)2+(х+2)2 12. у= х2 – х+6 13. у= х – 2|х| 14. у=5х2+7|х| 15. 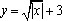 | Четные функции | Нечетные функции | Функции общего вида | |
|
|
| |
|
|
|
| Работа на постерах ФО критерии успеха: умеет определять четность, нечетность функции
|
| Самостоятельная работа 5-6 мин Приложение №5
| Тест Вариант 1 1.Найдите область определения функции у = 4х – х4 а) все числа, кроме 0; б) (0;+); в) (- ;+); г) (- 0]. 2. Задана функция у = 4х – х4. Найдите у(-1) а) -4; б) -5; в) 5; г) 4. 3. Какая из функций является четной: а а) у = х3 ; б) у = х4; в) у = х4-х3; г)у = х3+х4 ? 4. Какая из функций является нечетной: а) у = х3 ; б) у = х4; в) у = х4-х3; г)у = х3+х4 ? 5. Известно, что у = f(х) – нечетная функция и f(-3) = -5. Найдите f(3) а) 3; б) -3; в) 5; г) -5. 6. Известно, что у = f(х) – четная функция и f(2) = 43. Найдите f( -2) + f(2): а) 43; б) 0; в) -86; г) 86. 7. Какая из функций является ни четной, ни нечетной: а) у = х8 ; б) у = х5 -1; в) у = х7 ; г)у = х ?
| ФО критерии успеха: знает и умеет определять четность, нечетность функции
|
| Совместная работа это главная тщательно запланированная работа, так что Учащиеся менее уверенные работают с такими же как своего уровня, но очень уверенными. Диалог между партнерами таков, что оба учатся одновременно, а не так чтобы кто-то зависел от другого.
| Наблюдение Опрос Вопросы на понимание Взаимооценивание Самооценивание Рефлексия
| Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. Пункты, применяемые из Правил техники безопасности на данном уроке. |

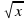
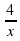
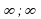 )
)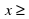 0
0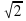
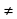 0
0