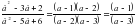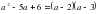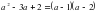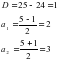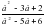8-сынып Алгебра
Та?ырыбы: Квадрат ?шм?ше. Квадрат ?шм?шені к?бейткіштерге жіктеу.
Ма?саты: 1. Квадрат ?шм?ше ??ымымен таныстыру. Квадрат ?шм?шені? т?бірлерін табу, квадрат ?шм?шені к?бейткіштерге жіктеу.
2. О?ушыларды ізденімпазды??а, білімге ??штарлы??а, ?з бетімен е?бектене білуге, ??ыптылы??а, ?з ?атесін таба білуге т?рбиелеу.
3. О?ушыларды? ой- ?рісін, есте са?тау ?абілеттерін, ?здігінен есептер шы?ару да?дыларын арттыру.
Саба?ты? т?рі: Жа?а та?ырыпты т?сіндіру.
?діс- т?сілдері: с?ра?- жауап, баяндау, мультимедиялы? технологияны ?олдану.
К?рнекілігі: Слайдтар, форматтар, таратпа материалдар, ба?алау кестесі.
Саба?ты? барысы:
- ?йымдастыру
- ?й тапсырмасын тексеру
- ?айталау
- Жа?а та?ырыпты т?сіндіру
- Бекіту
- Ба?алау, ?орытындылау
- ?йге тапсырма беру
?й тапсырмасыны? жауаптарын слайдпен салыстыра отырып тексеру.
№209
- Бірінші сан – х
Екінші сан – у
- =22-у (22-у)2+у2=250
484-44у+у2+у2=250
2у2-44у+234=0 /:2
у2 -22у+117=0
- =484-468=16
х1=22-13=9 х2=22-9=13
Жауабы: (9;13)
№212
- с= а-b=3
c2=a2+b2
а1=3+(-6)=-3 а2=3+3=6
Жауабы: (-3;-6) немесе (6;3)
?айталау с?ра?тарын слаудтан к?рсете отырып ?ткен та?ырыптарды ?айталау.
- Квадрат те?деуді? жалпы т?рі ?алай жазылады?
- Квадрат те?деулерді? ?андай т?рлері бар?
- Квадрат те?деуді? т?бірлерін табуды? ?андай формулалары бар?
- Дискриминантты? табыл?ан м?ніне ?арай те?деуді? неше т?бірі болатынын ?алай аны?тау?а болады?
- Келтірілген квадрат те?деуде р=2к ж?п сан болса, те?деуді? т?бірі ?андай формуламен табылады?
Жа?а та?ырыпты т?сіндіру.
7-сынып алгебра курсынан «к?пм?ше» ??ымымен таныссы?дар. Енді осындай к?пм?шені? бір т?рі «квадрат ?шм?ше» ??ымын ?арастырамыз.Квадрат ?шм?шені? т?бірлерін табу, квадрат ?шм?шені к?бейткіштерге жіктеуді ?йренесі?дер. Я?ни, б?гінгі ?тетін та?ырыбымыз «Квадрат ?шм?ше. Квадрат ?шм?шені к?бейткіштерге жіктеу».
Аны?тама: ах2+вх+с, а≠0 т?ріндегі к?пм?ше квадрат ?шм?ше деп аталады, м?нда?ы х-айнымалы, а,в-коэффициенттер, с- бос м?ше.
Егер а=1 болса, онда квадрат ?шм?ше келтірілген ?шм?ше деп аталады.
Квадрат ?шм?шені нольге айналдыратын х айнымалысыны? м?ндерін квадрат ?шм?шені? т?бірлері деп атайды. Я?ни, ах2+вх+с=0 те?деуіні? шешімдері квадрат ?шм?шені? т?бірлері деп аталады.
Квадрат ?шм?шені к?бейткіштерге жіктеу ?шін жалпы т?рдегі ах2+вх+с=0, а≠0 (1) квадрат те?деуі берілсін. Те?деуді? екі жа? б?лігін а-?а б?лу ар?ылы (2) келтірілген квадрат те?деуін аламыз. х1, х2 осы те?деуді? т?бірлері болсын. Виет теоремасы бойынша
b,с- ны? табыл?ан м?ндерін (1) формула?а ?оямыз. Сонда
ах2+вх+с=ах2-а(х1 +х2 )х+а(х1х2 )=а(х2-( х1+х2)х+х1х2 ) =а(х2-х1х-х2х+х1х2)=а(х(х-х1)-х2(х-х1))=а(х-х1)(х-х2)
Я?ни ах2+вх+с=а(х-х1)(х-х2) (3) формуласын аламыз. Осы формула бойынша квадрат ?шм?шені к?бейткіштерге жіктеуге болады.
Демек, квадрат ?шм?шені? т?бірлері бар болса, онда ол к?бейткіштерге жіктеледі. Ж?не керісінше егер квадрат ?шм?ше к?бейткіштерге жіктелсе, онда оны? т?бірлері бар болады деген т?жырым да д?рыс болады.
Мысалы: 3х2+4х-7=0 квадрат ?шм?шесін к?бейткіштерге жіктейміз. Ол ?шін дискриминантты тауып, квадрат те?деуді? шешімдерін табамыз. Н?тижесінде 3х2+4х-7=3(х-1)(х+ )
ах2+вх+с=0, а≠0 квадрат ?шм?шені? е? ?лкен ж?не е? кіші м?ндерін аны?тау ?шін, алдымен квадрат ?ш?шені? толы? квадратын айыру керек. Одан кейін квадрат ?шм?шедегі1-ші коэффициентті? та?басын аны?таймыз.
а>0 болса, квадрат ?шм?шені? е? кіші м?ні
а<0 болса, квадрат ?шм?шені? е? ?лкен м?ні болады.
Мысалы: -х2+6х-8=-(х2+6х+8)=-(х2+6х+9-1)=-((х-3)2-1)=1-(х-3)2
Т?ра?ты азай?ышы бар екім?шені? айырымыны? м?ні азайт?ышты? е? кіші м?нінде е? ?лкен м?нді ?абылдайды. х=3 бол?анда, азайт?ышты? м?ні е? кіші м?н болады. Демек х=3 бол?анда 1-(3-3)2=1-0=1 квадрат ?шм?шені? е? ?лкен м?ні бар ж?не ол 1-ге те?.
Та?тамен ж?мыс: №230 (1,2)
Д?птермен ж?мыс: №232 (1,4)
Схема бойынша есептеу: №237 (1)
Б?лшекті ?ыс?арт
Б?лшекті ?ыс?арт
Ба?алау.
?орытындылау.
- Квадрат ?шм?ше мен квадрат те?деуді? арасында ?андай ??састы? ж?не айырмашылы? бар?
- ?андай жа?дайда квадрат ?шм?ше сызы?ты? к?бейткіштерге жіктелмейді?
- ?ай уа?ытта квадрат ?шм?ше келтірілген деп аталады?
?йге тапсырма: §12. №231(1,3), №233(3,4)
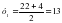
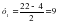
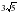 а-b=3
а-b=3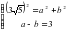
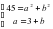
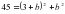
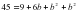
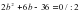
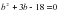
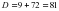
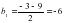
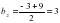
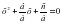 (2) келтірілген квадрат теңдеуін аламыз. х1, х2 осы теңдеудің түбірлері болсын. Виет теоремасы бойынша
(2) келтірілген квадрат теңдеуін аламыз. х1, х2 осы теңдеудің түбірлері болсын. Виет теоремасы бойынша 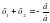
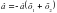
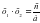
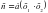
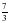 )
)