Коспект урока геометрии 9 класс и презентация.

3,5 м

Рассчитайте, сколько надо краски, что бы покрасить пол такой формы в 2 слоя из расчета 90 г/м².

Урок геометрии в 9-м классе по теме "Площадь параллелограмма"

Цели и задачи урока:

• Повторить свойства площадей фигур; формулы площади прямоугольника и квадрата; вывести формулу для нахождения площади параллелограмма; рассмотреть задачи с её применением.

• Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.

• Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Оборудование: компьютер, мультимедийный проектор. Урок проводится с использованием мультимедийной презентации Power Point.

План урока.

1. С помощью компьютерной презентации актуализация знаний учащихся и постановка проблемной ситуации;

2. Объяснение нового материала и решение задач;

3. Контроль знаний учащихся;

4. Рефлексия;

5. Домашнее задание.

Ход урока

Учитель: - Здравствуйте ребята. Повторим известные нам свойства площадей, изученные формулы площадей некоторых видов многоугольников, применение их при решении задач. Посмотрите на картинку слайда: какие свойства геометрических фигур иллюстрируют следующие рисунки?

Учащиеся после просмотра очередного рисунка формулируют свойство:

1. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

2. Равные фигуры имеют равные площади.

3. Площадь квадрата равна квадрату его стороны.

- Сформулируйте правила вычисления площади прямоугольника. (Площадь прямоугольника равна произведению смежных сторон).

- На какие теоремы, определения и свойства мы опирались при доказательстве теоремы о площади прямоугольника? (При доказательстве теоремы мы опирались на формулу площади квадрата, на формулы сокращенного умножения (квадрат суммы), на свойства площадей многоугольников). Слайд1

- Вам предлагается решить задачи. Дети решают устно задачи по готовому чертежу.

(Слайд 2-3)

В ходе изучения четырехугольников мы уже выполняли практические задания по “перекраиванию” различных фигур. Сейчас я предлагаю вам выполнить следующие перекраивания геометрических фигур. (Слайд 4-5)

- Давайте посмотрим, что у вас получилось.

1) Что сохранилось у прямоугольника и треугольника?

2) Как называются такие фигуры?

(Учащиеся рассказывают о “перекраивании” прямоугольника и трапеции, делая необходимые пояснения. Сохранились площади. Равновеликие фигуры).

-Подвести учащихся к целеполаганию через использование исторической справки о налогах за использование земельного участка;(Слайд 6)

1.Историческая задача (учебная беседа) . В древнее время, после каждого разлива Нила египетским земледельцам приходилось заново разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площадь различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараона, которые собирали с земледельцев налоги. Как же быть, если не каждое поле можно разбить на прямоугольники и квадраты?

Актуальна ли эта проблема в наше время?

2.

Предположим, что участки стали такой формы? (Слайд 7)

Обсудите в парах:

как найти площадь каждой из этих фигур?

Какие измерения нужно выполнить?

Определяют форму участка

и предлагают способы вычисления площади участков.

В чем разница между нахождением площади прямоугольника и параллелограмма?

Какое открытие мы сделали?

Какая же цель у нас сегодня на уроке?

Записываем тему урока.(На доске)

-Дети формулируют цели урока.

Записывают тему урока в тетради.

Учитель: Давайте попробуем исследовать вопрос о площади параллелограмма и найти способ ее вычисления, используя известные на сегодняшний день формулы площадей многоугольников.(слайд 9-10)

Напомню вам, как правильно строить высоты параллелограмма.(Слайд11-13)

Закрепление полученных знаний(Слайд14-30).

Обучающая самостоятельная работа(если останется время).(Слайд31)

В параллелограмме АВСD высота СМ разбивает сторону АD на отрезки АМ и DМ. Найдите его площадь, если:

Вариант 1 Вариант 2

АВ=13, АМ=10, DМ=5 СD=15, ВС=16, АМ=7.

Подведение итогов. Постановка домашнего задания.

- В начале урока нами была выявлена цель, напомните её пожалуйста.

(исследовать параллелограмм с целью изучения формулы для нахождения его площади)

- достигли ли мы поставленной цели?

(Да)

- Что мы использовали для достижения цели урока?

(Известные нам свойства площадей многоугольников, формулу площади прямоугольника).

- Запишите домашнее задание(задачи подобные тем, что решали на уроке, поэтому пояснения не требуют ). (Слайд 32)

Спасибо за урок!

1. Какие свойства площадей геометрических фигур иллюстрируют следующие рисунки?

Рисунок 1

Рисунок 2

Рисунок 3

2. Как вычислить площадь прямоугольника?

S прям = ab

3. На какие теоремы, определения и свойства мы опирались при доказательстве теоремы о площади прямоугольника?

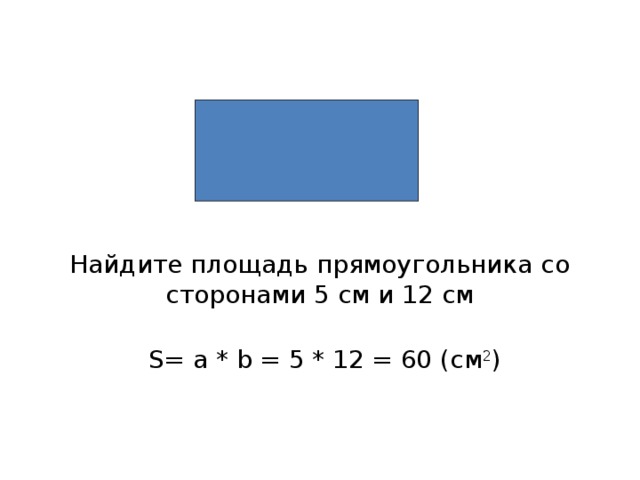
Найдите площадь прямоугольника со сторонами 5 см и 12 см

S= a * b = 5 * 12 = 60 ( см 2 )

Решите задачу.

Дано : АВС D – прямоугольник.

В D = 8 см., D С = 6 см.,

∠ В D С = 30 º .

Найти : S ( АВС D )

А

В

8

30º

D

С

6

S ( АВС D ) = 24 см²

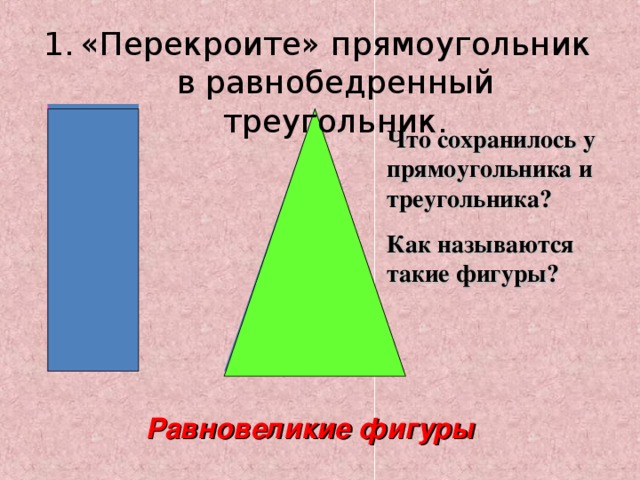
• «Перекроите» прямоугольник в равнобедренный треугольник.

Что сохранилось у прямоугольника и треугольника?

Как называются такие фигуры?

Равновеликие фигуры

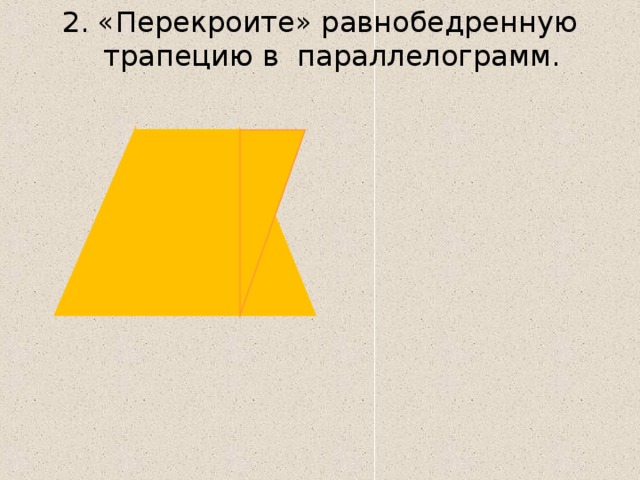
2. «Перекроите» равнобедренную трапецию в параллелограмм.

• Историческая задача (учебная беседа) . В древнее время, после каждого разлива Нила египетским земледельцам приходилось заново разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площадь различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараона, которые собирали с земледельцев налоги. Как же быть, если не каждое поле можно разбить на прямоугольники и квадраты?
• Актуальна ли эта проблема в наше время?

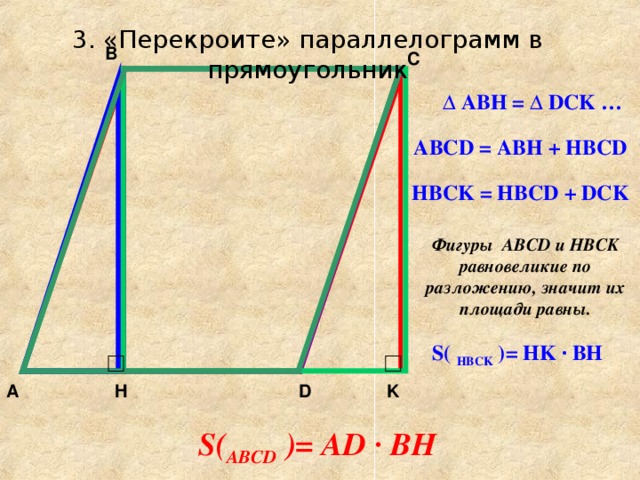
3. «Перекроите» параллелограмм в прямоугольник

B

C

∆ ABH = ∆ DCK …

ABCD = ABH + HBCD

HBCK = HBCD + DCK

Фигуры ABCD и HBCK равновеликие по разложению, значит их площади равны.

S ( HBCK ) = HK · BH

D

A

H

K

S ( ABCD ) = AD · BH

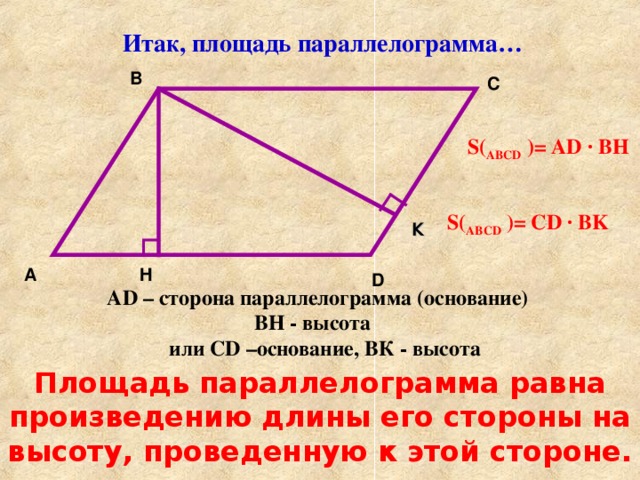
Итак, площадь параллелограмма…

B

C

S ( АВС D ) = AD · BH

S ( АВС D ) = CD · BK

К

H

A

D

AD – сторона параллелограмма (основание)

ВН - высота

или CD –основание, ВК - высота

Площадь параллелограмма равна произведению длины его стороны на высоту, проведенную к этой стороне.

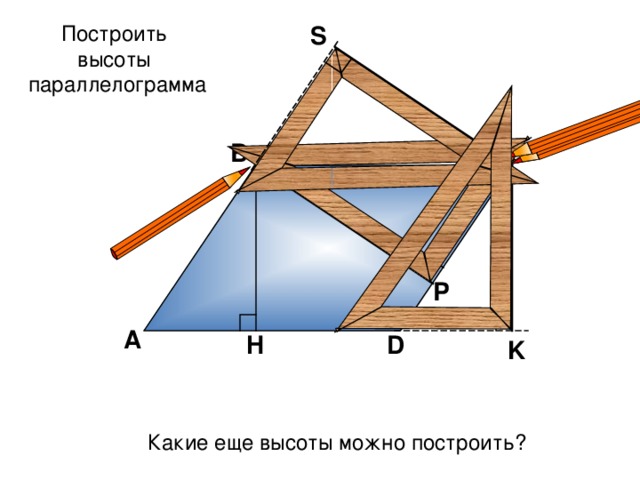
Построить

высоты

параллелограмма

S

В

С

Р

А

H

D

K

Какие еще высоты можно построить?

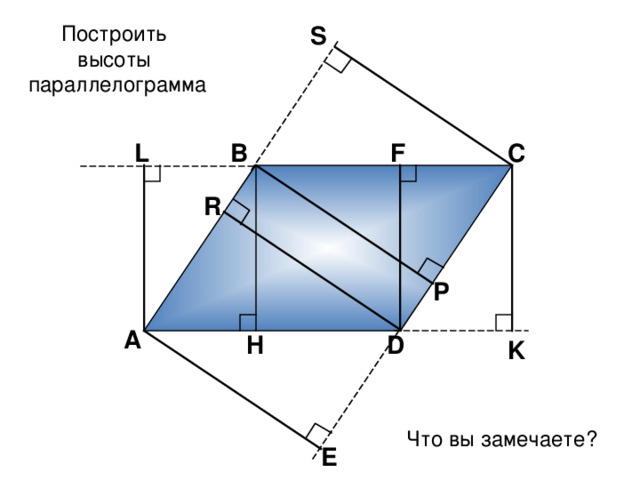
Построить

высоты

параллелограмма

S

L

С

F

В

R

Р

Высоты, проведенные из вершины острого угла, лежат во внешней области параллелограмма. Высоты. проведенные из вершин тупых углов, лежат во внутренней области параллелограмма. Есть равные высоты. Почему они равны?

А

H

D

K

Что вы замечаете?

E

12

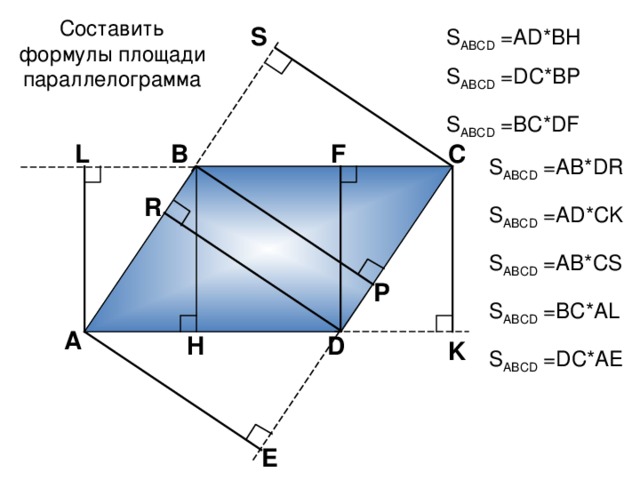
Составить формулы площади параллелограмма

S

S ABCD = А D*BH

S ABCD =DC*BP

S ABCD =BC*DF

L

С

В

F

S ABCD =AB*DR

R

S ABCD =AD*CK

S ABCD =AB*CS

Р

S ABCD =BC*AL

А

H

D

K

S ABCD =DC*AE

E

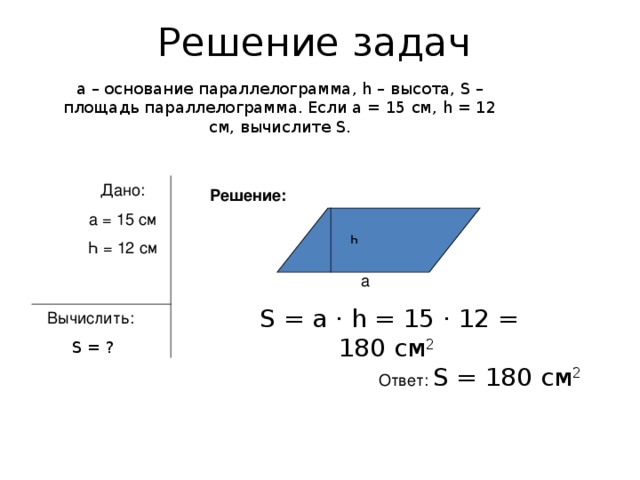
Решение задач

а – основание параллелограмма, һ – высота, S – площадь параллелограмма. Если а = 15 см, һ = 12 см, вычислите S .

Дано:

а = 15 см

Һ = 12 см

Решение:

һ

а

S = а · һ = 15 · 12 = 180 см 2

Вычислить:

S = ?

Ответ: S = 180 см 2

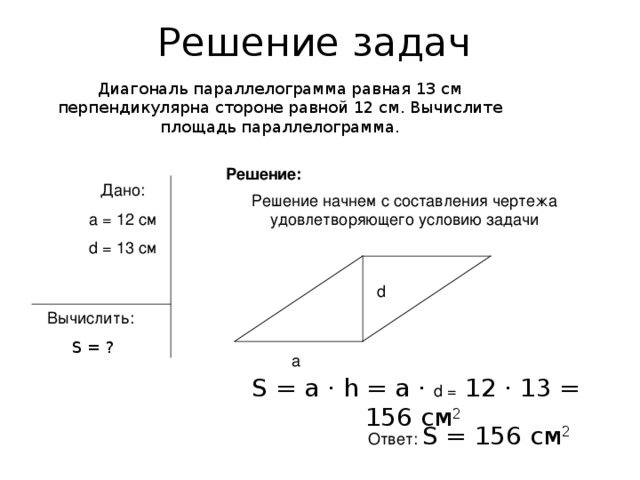
Решение задач

Диагональ параллелограмма равная 13 см перпендикулярна стороне равной 12 см. Вычислите площадь параллелограмма.

Решение:

Дано:

a = 12 см

d = 13 см

Решение начнем с составления чертежа удовлетворяющего условию задачи

d

Вычислить:

S = ?

а

S = а · һ = а · d = 12 · 13 = 156 см 2

Ответ: S = 156 см 2

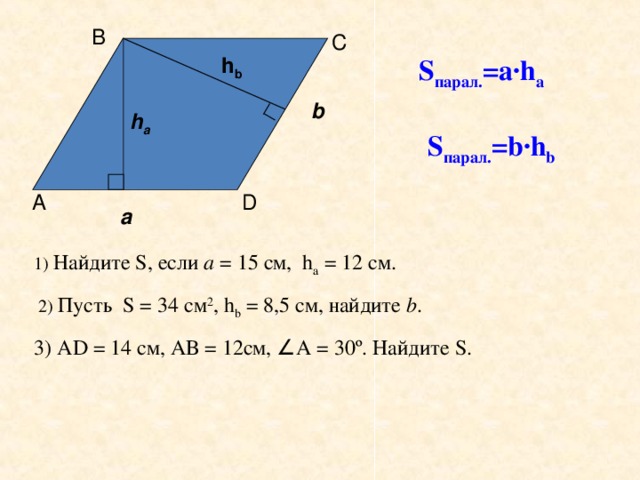
В

С

h b

S парал. =а ·h a

b

h a

S парал. = b·h b

А

D

а

1) Найдите S , если а = 15 см, h a = 12 см.

2) Пусть S = 34 см 2 , h b = 8,5 см, найдите b .

3) А D = 14 см, АВ = 12см, ∠ А = 30 º . Найдите S .

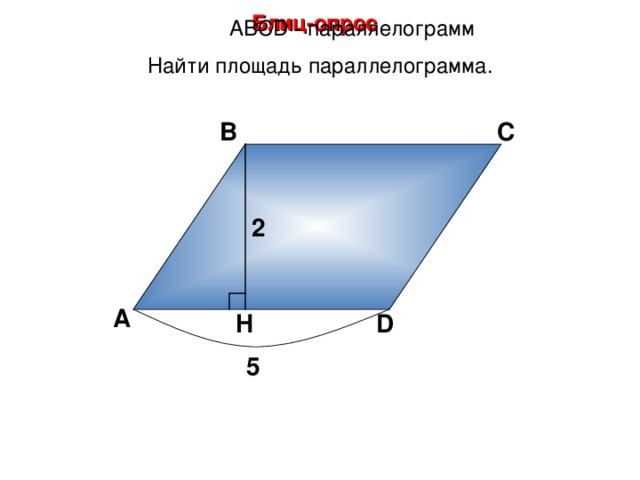
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

В

С

2

А

D

H

5

17

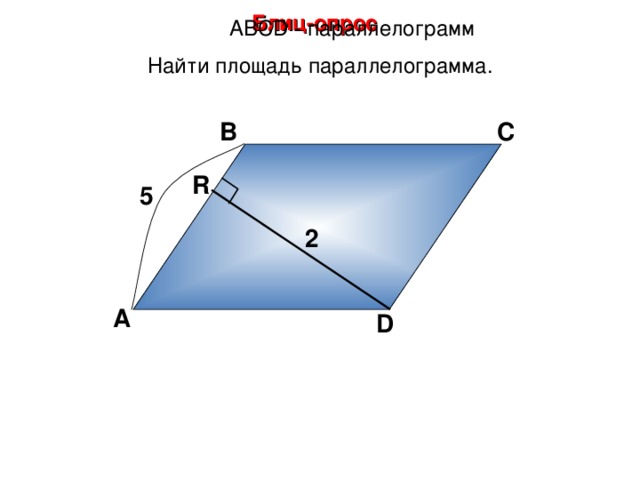
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

В

С

R

5

2

А

D

18

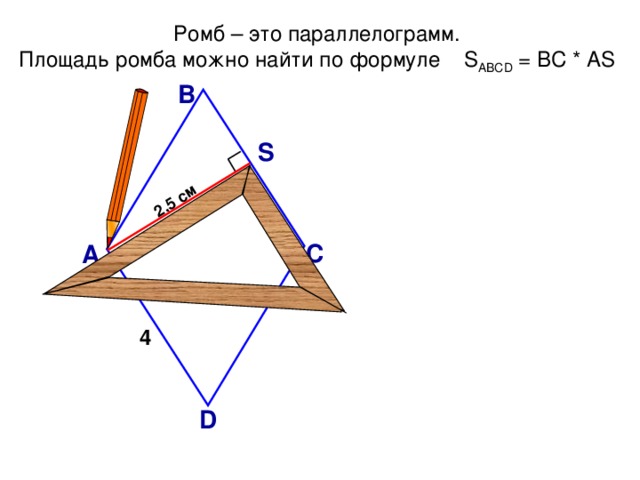
2 ,5 см

Ромб – это параллелограмм.

Площадь ромба можно найти по формуле S АВС D = ВС * А S

В

S

С

А

4

D

19

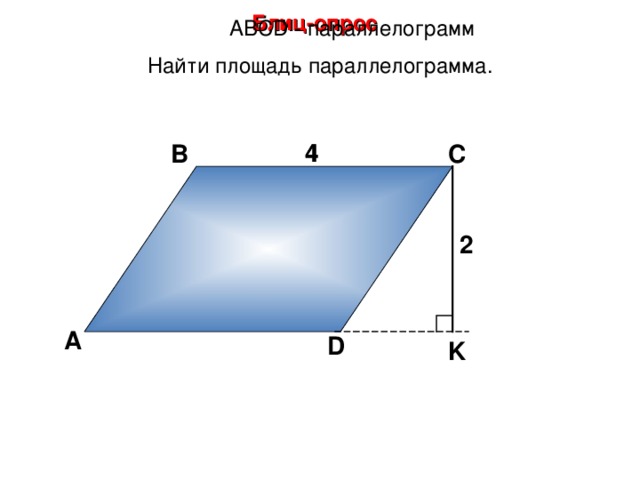
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

4

4

В

С

2

А

D

K

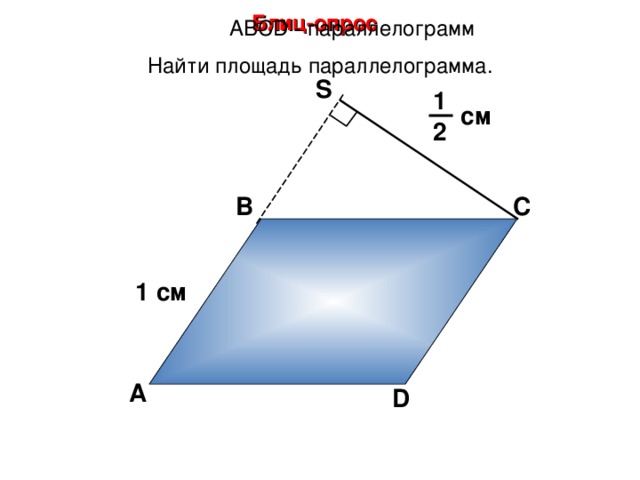
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

S

1

см

2

В

С

1 см

А

D

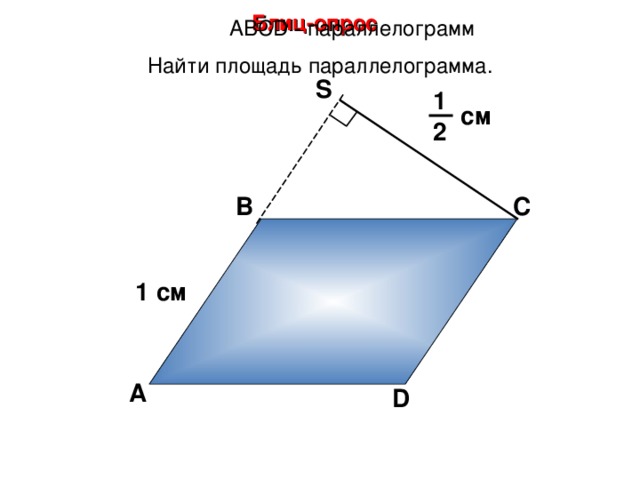
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

S

1

см

2

В

С

1 см

А

D

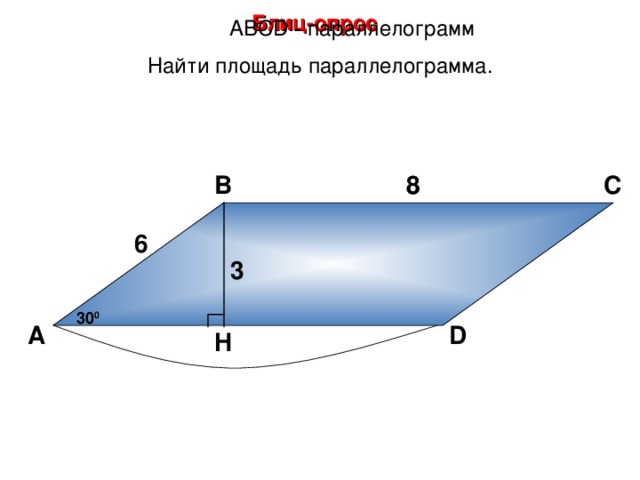
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

В

С

8

8

6

3

30 0

А

D

H

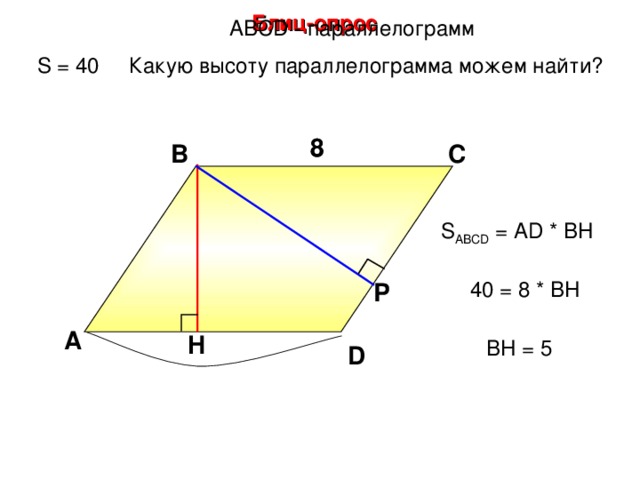
Блиц-опрос

А BCD - параллелограмм

S = 40 Какую высоту параллелограмма можем найти?

8

8

В

С

S ABCD = А D * BH

40 = 8 * BH

Р

А

H

BH = 5

D

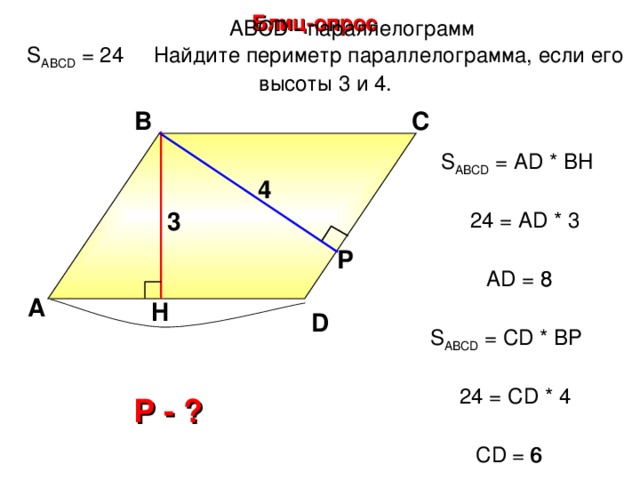
Блиц-опрос

А BCD - параллелограмм

S ABCD = 2 4 Найдите периметр параллелограмма, если его высоты 3 и 4.

В

С

S ABCD = А D * BH

4

3

24 = AD * 3

Р

8

AD = 8

А

H

D

Л.И. Звавич, Е.В. Потоскуев «Тестовые задания по геометрии»

S ABCD = С D * B Р

24 = С D * 4

Р - ?

С D = 6

6

25

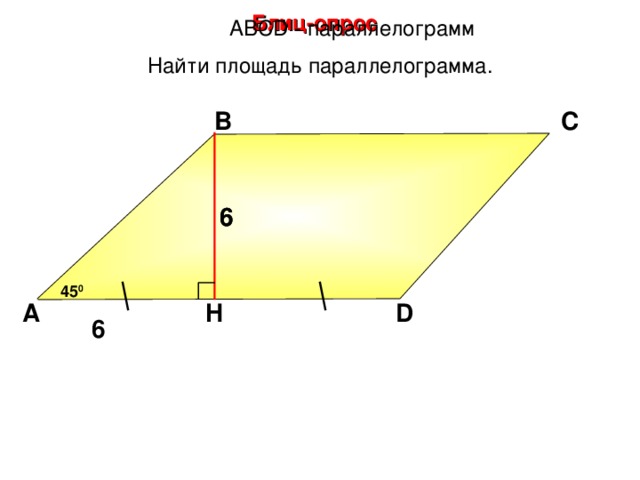
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

В

С

6

6

45 0

D

H

А

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

6

26

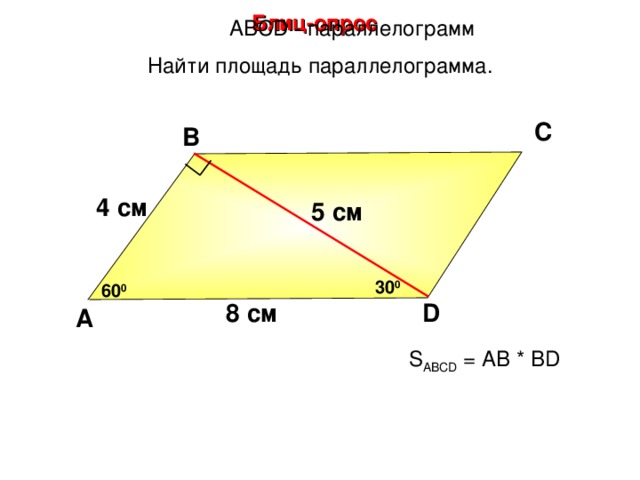
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

С

В

4 см

5 см

30 0

60 0

D

8 см

А

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

S ABCD = АВ * BD

26

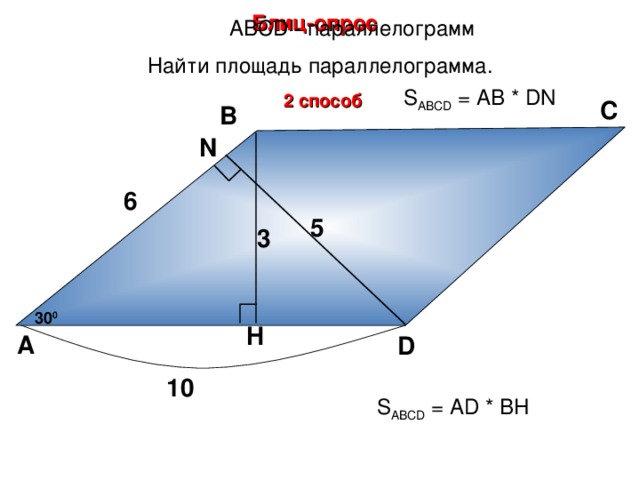
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

S ABCD = А B * DN

2 способ

С

В

N

6

5

3

30 0

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

H

А

D

10

S ABCD = А D * BH

28

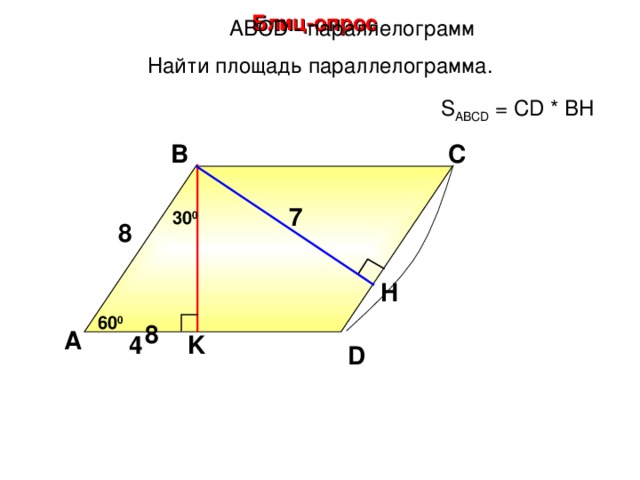
Блиц-опрос

А BCD - параллелограмм

Найти площадь параллелограмма.

S ABCD = CD * BH

С

В

7

3 0 0

8

H

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

60 0

8

А

4

K

D

29

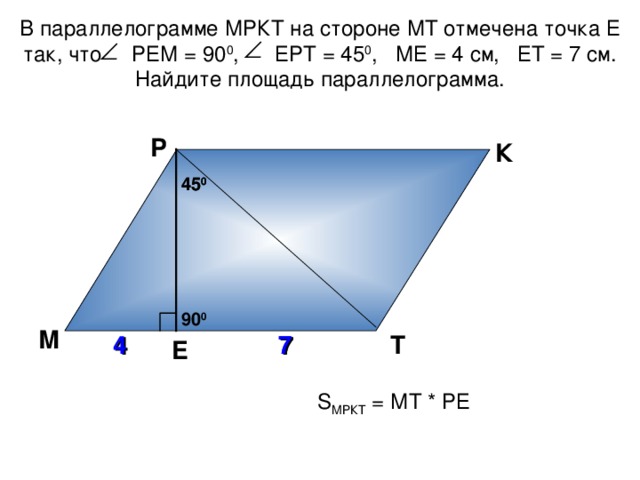
В параллелограмме МРКТ на стороне МТ отмечена точка Е так, что РЕМ = 9 0 0 , ЕРТ = 45 0 , МЕ = 4 см, ЕТ = 7 см. Найдите площадь параллелограмма.

Р

К

45 0

45 0

90 0

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 8 класса»

М

7

7

Т

4

Е

S МРКТ = МТ * РЕ

30

Обучающая самостоятельная

В параллелограмме АВС D высота СМ разбивает сторону А D на отрезки АМ и D М. Найдите его площадь, если:

Вариант 1 Вариант 2

АВ=13, АМ=10, D М=5 С D =15, ВС=16, АМ=7 .

Итоги урока

• Достигли ли мы поставленной цели?
• Какой главный итог нашего урока?
• Что мы использовали для достижения цели урока?

Домашнее задание:

п.123,

№ 11, №12, №9

завершение

дополнительно

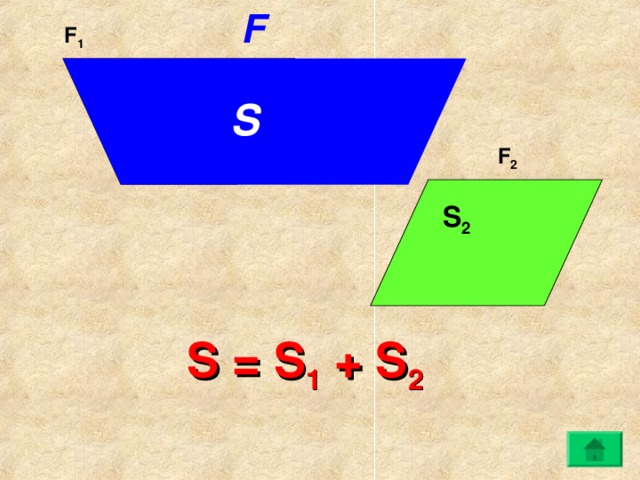
F

F 1

S

S 1

F 2

S 2

S = S 1 + S 2

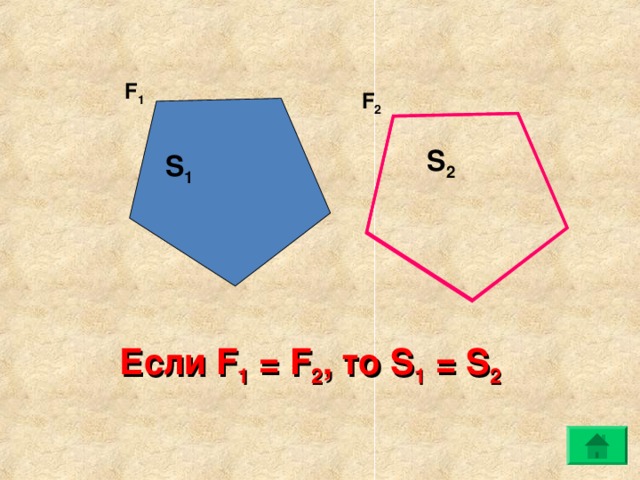
F 1

F 2

S 2

S 1

Если F 1 = F 2 , то S 1 = S 2

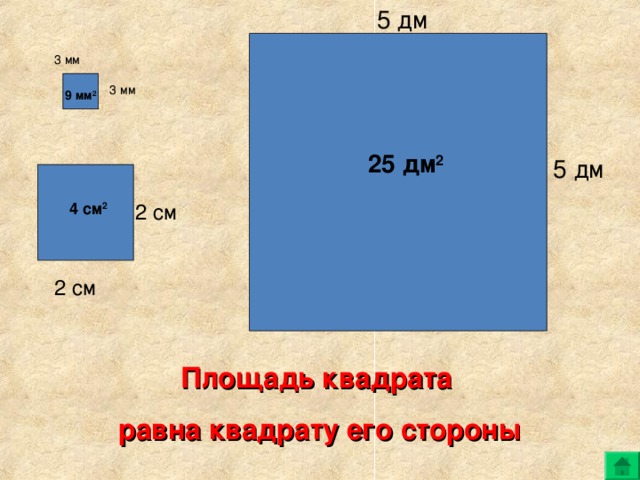
5 дм

3 мм

3 мм

9 мм 2

25 дм 2

5 дм

2 см

4 см 2

2 см

Площадь квадрата

равна квадрату его стороны