| - Здравствуйте, ребята! Посмотрите на рисунок и скажите, что за объемные фигуры изображены на рисунке? -Дайте определение многогранника.
-Какие из изображенных многогранников вам известны?
-На какие две группы можно разделить эти многогранники? Какие многогранники называют выпуклыми? Определим, какие многогранники будут выпуклыми, а какие невыпуклыми. Почему 3,6,7 невыпуклые? - Что мы знаем о сумме всех плоских углов при каждой вершине выпуклого многогранника?
- Какая фигура лежит в основании данного многогранника? -Чему равна сумма углов в многоугольнике? - Давайте подсчитаем, чему равна сумма всех углов в правильном шестиугольнике? Каждого угла шестиугольника? Это нам сегодня понадобиться для изучения новой темы. - Однажды Л.Н. Толстой сказал: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?».
-С симметрией мы встречаемся в природе, архитектуре, технике, быту. Мы часто видим симметричные творения природы (листья, цветы, птицы, животные) или творения человека (здания, техника) - все то, что окружает нас каждый день. В быту: молотки, рубанки, лопаты, трубы. Мы смотрим на себя в зеркало и видим, что части нашего лица симметричны друг другу. По улицам ездят автомобили, автобусы, правая и левая части которых симметричны. Таким образом, симметрия бывает не только на плоскости (кленовый лист), но и в пространстве (лицо).
Ребята, для начала вспомним такие понятия, как симметрия относительно точки, симметрия относительно прямой, которые мы изучили на плоскости. -Какие же точки называются симметричными относительно точки?
При этом точку О называют центром симметрии. - Сформулируйте определение точек симметричных относительно прямой.
При этом прямую а называют осью симметрии. По аналогии с симметрией на плоскости определятся симметрия в пространстве. Симметрия тесно связана с многогранниками. Цель нашего урока: расширить знания о симметрии и многогранниках. Тему урока мы запишем в процессе заполнения таблиц. |
На рисунке изображены многогранники.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником.
Правильная призма (1), наклонная призма(4), пирамида треугольная (2), пятиугольная (5). На выпуклые и невыпуклые многогранники. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Выпуклые:1,2,4,5, невыпуклые:3,6,7.
Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше .
В основании данного многогранника лежит правильный шестиугольник. Сумма углов в многоугольнике равна . Сумма всех углов в правильном шестиугольнике равна . Каждый угол равен .
Точки и называются симметричными относительно точки О, если О - середина отрезка .
Точки называются симметричными относительно прямой а, если прямая а проходит через середину отрезка и перпендикулярна к этому отрезку.
| (слайд 1) (слайд 2)
(слайд 3)
(слайд 4)
(слайд 5)
(слайд 6)
(слайд 7 -11)
(слайд 12)
(слайд 13) |
| - Как было сказано выше, по аналогии с симметрией на плоскости определятся симметрия в пространстве. Поэтому в процессе работы заполним следующую канву – таблицу. Мы вспомнили определение точек симметричных относительно точки. Попробуйте сформулировать такое определение только для симметричных точек в пространстве. Чем будет точка О? - А как формулируется определение точек симметричных относительно прямой в пространстве?
Чем будет являться прямая а? - В пространстве существует понятие точек симметричных относительно плоскости. Попытайтесь дать определение.
Значит, плоскость- плоскость симметрии. Итак, точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Таким образом, в пространстве помимо центральной и осевой симметрии, которые есть на плоскости, добавляется зеркальная симметрия.
-Оказывается у некоторых многогранников тоже есть центр, ось и плоскость симметрии, которые называют элементами симметрии этого многогранника. -Рассмотрим два многогранника: куб и параллелепипед. Куб называют правильным многогранником. Давайте выясним почему? Давайте подсчитаем, сколько ребер сходиться в каждой вершине куба, параллелепипеда. Чем являются грани этих многогранников? Особо важно, что все грани куба равны между собой, а у параллелепипеда не все грани равны между собой. Таким образом, куб будем относить к правильным многогранникам.
- Посмотри на следующий рисунок. Давайте попробуем определить является ли одна из этих пирамид правильным многогранником. Действуем по той же схеме (определяем число ребер сходящихся в каждой вершине, вид граней и их равенство). Попробуйте дать определение правильного многогранника. Определение. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходиться одно и тоже число ребер. - Возникает вопрос, сколько граней, являющихся правильными многоугольниками, может сходиться в одной вершине, чтобы в результате получился правильный многогранник. Давайте подсчитаем, а полученные результаты будет сравнивать с , так как по теореме, которую мы вспоминали в начале урока сумма всех плоских углов при каждой вершине выпуклого многогранника меньше . 1. Рассмотрим правильный треугольник. Сколько градусов равен каждый угол? Подсчитаем сумму плоских углов при вершине треугольника, если: а) в каждой вершине сходится три грани; Сумма меньше , значит, такой правильный многогранник может быть. б) в каждой вершине сходится четыре грани; Сумма меньше , значит, такой правильный многогранник может быть. в) в каждой вершине сходится пять граней; Сумма меньше , значит, такой правильный многогранник может быть. г) в каждой вершине сходится шесть граней; Сумма равна , противоречит теореме. Следовательно, такого многогранника не может быть. 2. Рассмотрим правильный четырехугольник – квадрат. Сколько градусов равен каждый угол? Подсчитаем сумму плоских углов при вершине квадрата, если: а) в каждой вершине сходится три грани; Сумма меньше , значит, такой правильный многогранник может быть. б) в каждой вершине сходится четыре грани; Сумма равна , противоречит теореме. Следовательно, такого многогранника не может быть. 3. Рассмотрим правильный пятиугольник. Сколько градусов равен каждый угол? Подсчитаем сумму плоских углов при вершине квадрата, если: а) в каждой вершине сходится три грани; Сумма меньше , значит, такой правильный многогранник может быть. б) в каждой вершине сходится четыре грани, очевидно, что сумма равна , противоречит теореме. Следовательно, такого многогранника не может быть. Если будем рассматривать правильный шестиугольник, то сумма плоских углов при каждой вершине, в которой сходится три грани, будет равна . Это тоже противоречит теореме. Исходя из наших расчетов, можно сделать предположение, что не существует многогранника, гранями которого являются правильные шестиугольники. Верно ли это предположение?
-Ответ на этот вопрос дает следующая теорема. Сформулируем и докажем ее. Теорема. Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n6. Доказательство: Угол правильного n-угольника при n6 не меньше . Почему? (обратить внимание учеников на подсчеты в начале урока).
При каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n6, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем . Это невозможно. Почему? (так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше .
Из этого условия сделаем следующий важный вывод: каждая вершина правильного многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников. Других возможностей нет. В соответствии с этим выводом получаем следующие виды правильных многогранников: правильный тетраэдр; правильный октаэдр; правильный икосаэдр; куб; правильный додекаэдр; Немного из истории. Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона «Тимаус» (427 -347 до н.э.). Поэтому правильные многогранники также называют «платоновыми телами». Каждый из правильных многогранников, а их всего пять, Платон ассоциировал с четырьмя «земными» элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с «неземным» элементом – небом (додекаэдр). Рассмотрим виды правильных многогранников и их элементы симметрии, заполняя следующую канву-таблицу (см. приложение). Эту таблицу мы заполним не полностью, продолжим заполнение на уроке – семинаре. |
Точки и называются симметричными относительно точки О, если О - середина отрезка .
Точка О – центр симметрии. Точки называются симметричными относительно прямой а, если прямая а проходит через середину отрезка и перпендикулярна к этому отрезку. Прямая а – ось симметрии. Точки называются симметричными относительно плоскости , если плоскости проходит через середину отрезка и перпендикулярна к этому отрезку.
По три ребра в каждой вершине.
Грани куба – квадраты (правильные многоугольники), грани параллелепипеда – прямоугольники (неправильные многоугольники).
Обсуждение предложенных вариантов.
Каждый угол в правильном треугольнике равен .
Если в каждой вершине сходится три грани, то сумма плоских углов при вершине равна .
Если в каждой вершине сходится четыре грани, то сумма плоских углов при вершине равна .
Если в каждой вершине сходится пять граней, то сумма плоских углов при вершине равна .
Если в каждой вершине сходится шесть граней, то сумма плоских углов при вершине равна .
Каждый угол в квадрате равен .
Если в каждой вершине сходится три грани, то сумма плоских углов при вершине равна .
Если в каждой вершине сходится четыре грани, то сумма плоских углов при вершине равна .
Каждый угол в правильном пятиугольнике равен .
Если в каждой вершине сходится три грани, то сумма плоских углов при вершине равна .
Так как угол в правильном шестиугольнике равен , следовательно, меньше угол правильного n-угольника при n6 быть не может.
Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше | | Симметрия | | На плоскости | В пространстве | |
| |
| |
|
| (слайд 14)
Заполненная канва – таблица: | Симметрия | | На плоскости | В пространстве | | Две точки называются симметричными относительно данной точки (центра симметрии), если данная точка является серединой соединяющего их отрезка. | | Точки А и А1 называются симметричными относительно прямой а (оси симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к нему. | |
| Точки А и А1 называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. |
(слайд 15)
(слайд 16)
(слайд 17)
(слайд 18)
(слайд 19)
(слайд 20)
|

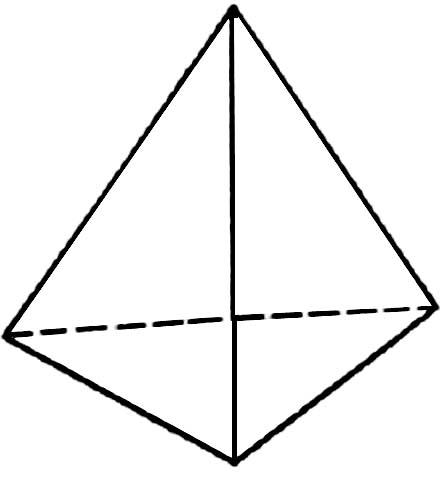 Тетраэдр
Тетраэдр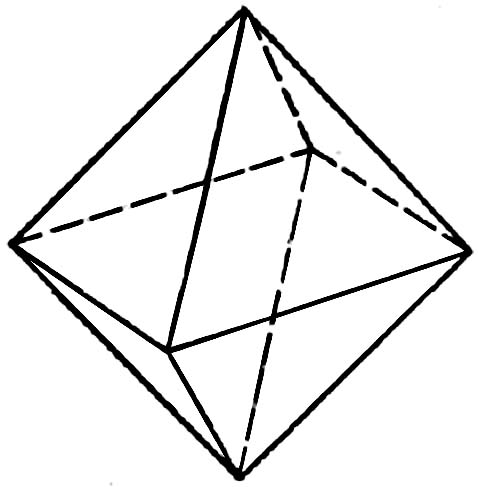 Октаэдр
Октаэдр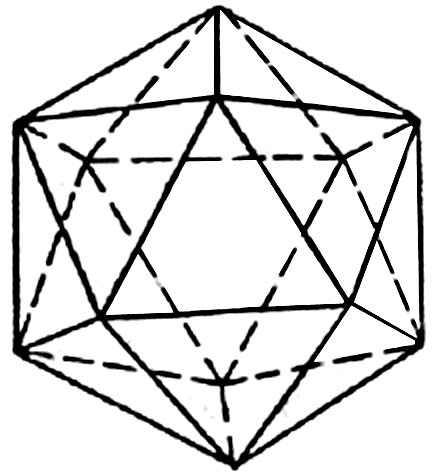 Икосаэдр
Икосаэдр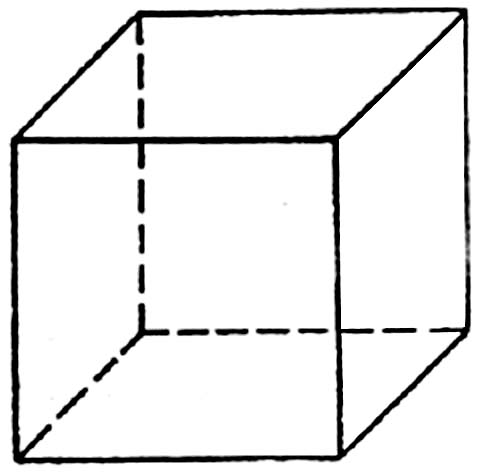
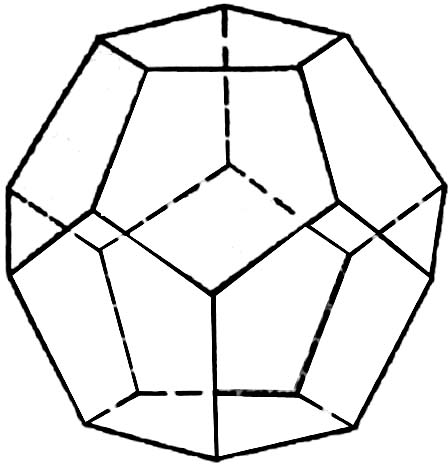 Додекаэдр
Додекаэдр















