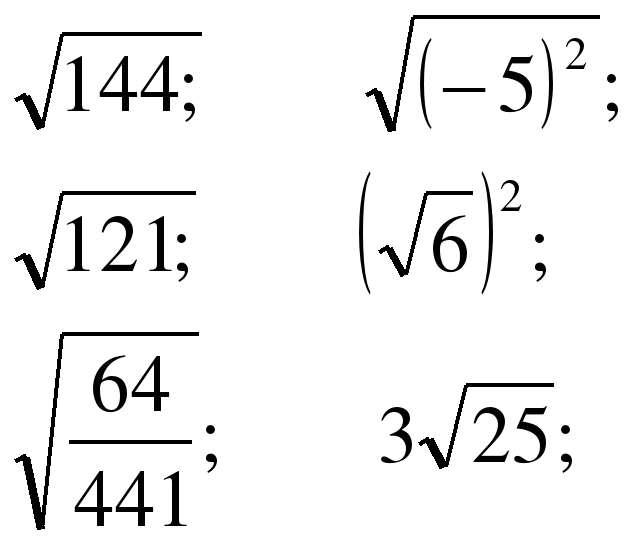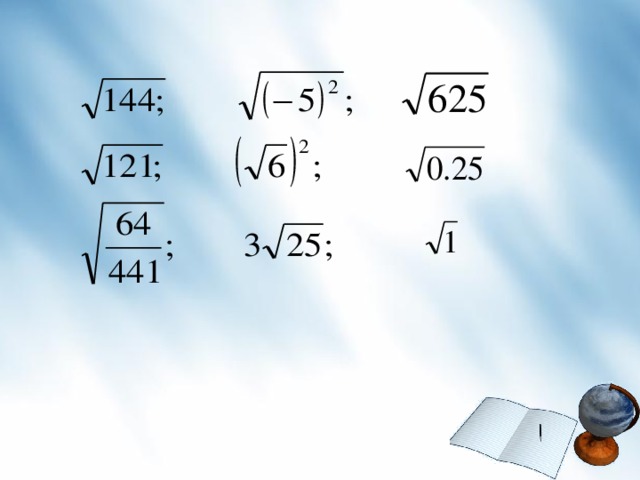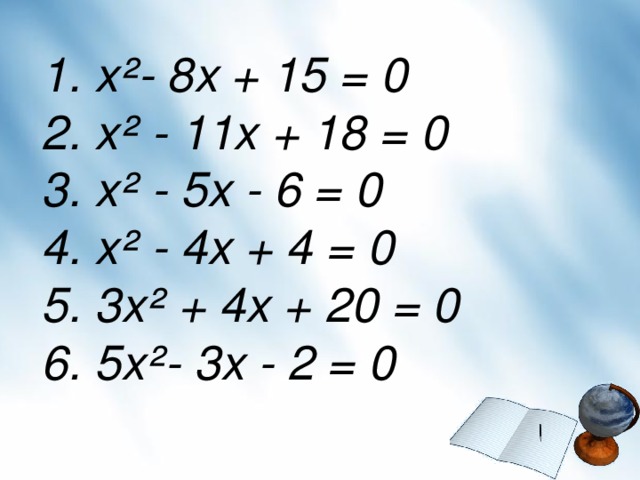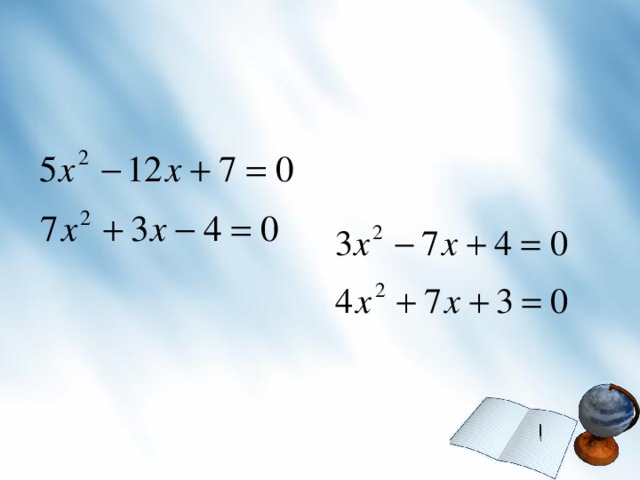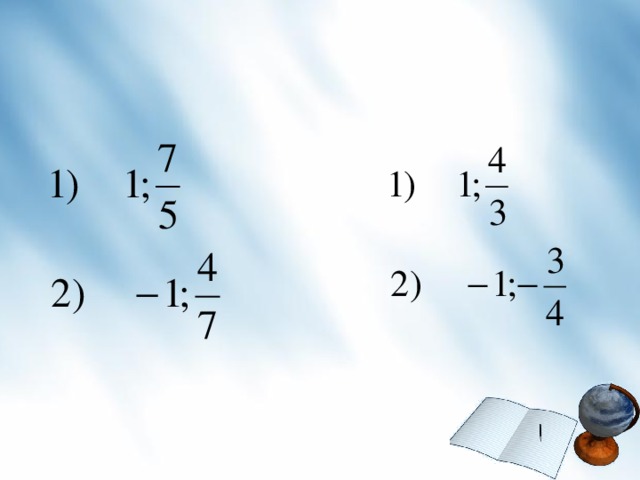Конспект урока математики на тему:"Квадратные уравнения"

Тема: Квадратные уравнения.

Эпиграф к уроку: "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".

Паскаль

Цели:

1. Показать уровень усвоения программного материала по теме «Квадратные уравнения», навыки решения квадратных уравнений с помощью применения формул корней квадратных уравнений, изучить новый способ решения квадратных уравнений.

2. Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического мышления,

3. Способствовать рациональной организации труда, внимательность, активное участие в учебно-познавательном процессе, самостоятельность, самокритичность.

Оборудование к уроку: тест "Квадратные уравнения", интерактивная доска, таблицы, карточки.

Ход урока

1. Организационный момент

Здравствуйте, ребята и гости нашего урока! Математику не зря называют "царицей наук", ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики - любознательность. Постараемся доказать это на уроке. Мы с вами начали изучать новый большой раздел «Квадратные уравнения»,

Эпиграфом к уроку я взяла слова великого математика Паскаля "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным". В течение урока мы еще вернемся к этим словам.

2.Эмоциональный настрой

Если день начинать с улыбки, то можно надеяться, что он пройдет удачно. Давайте сегодняшнее занятие проведем с улыбкой. Главная задача – быть внимательными, активными, находчивыми, а главное – трудолюбивыми. Показывать, что мы знаем и как умеем работать. 

3. Устный счет

Вычислить:

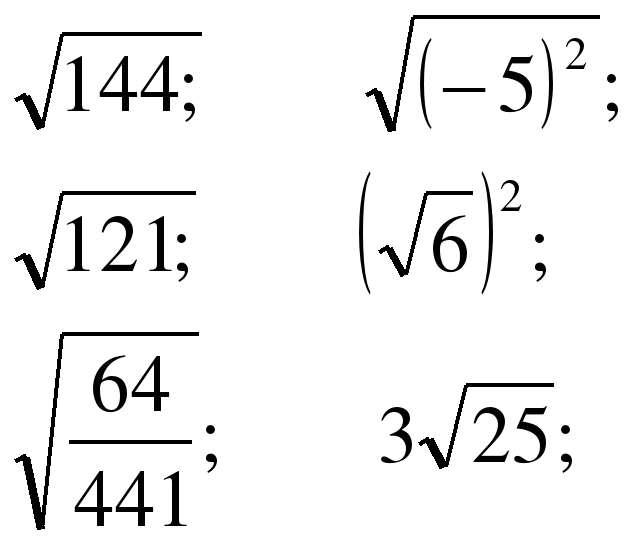
1. Актуализация знаний по теме квадратные уравнения

Виды уравнений

ЦОР №1289 на сайте e.edu.kz

Тест "Квадратные уравнения".

Итак, мы повторили, как можно решить квадратное уравнение. Сейчас я хотел бы проверить, как вы усвоили эти формулы и определения.

Ученики получают карточки с заданиями. Заполняют пропущенные слова в карточках.

I ВАРИАНТ

1. Уравнение вида 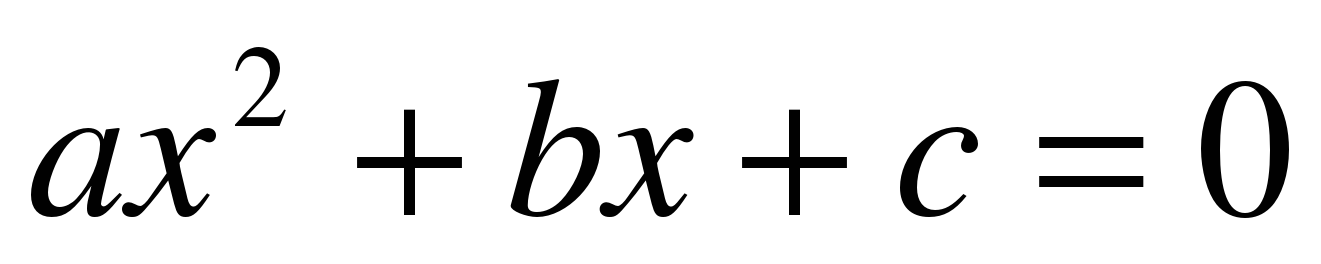, где a, b, c - заданные числа, a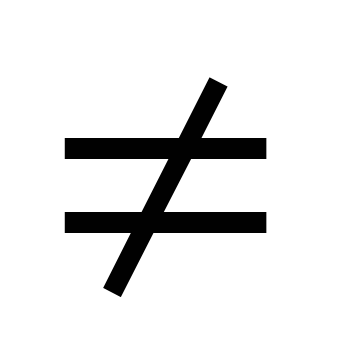0, x - переменная, называется...

2. Полное квадратное уравнение не имеет корней, если D ...

3. Уравнение вида 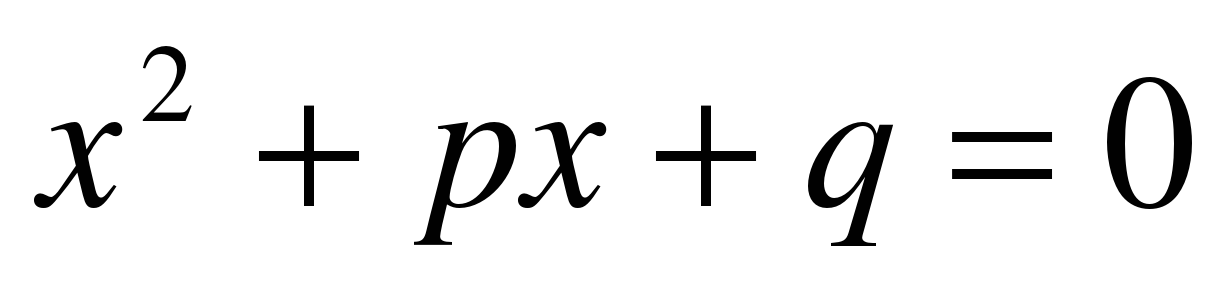называется...

4. Квадратное уравнение имеет два корня, если...

5. Дано уравнение 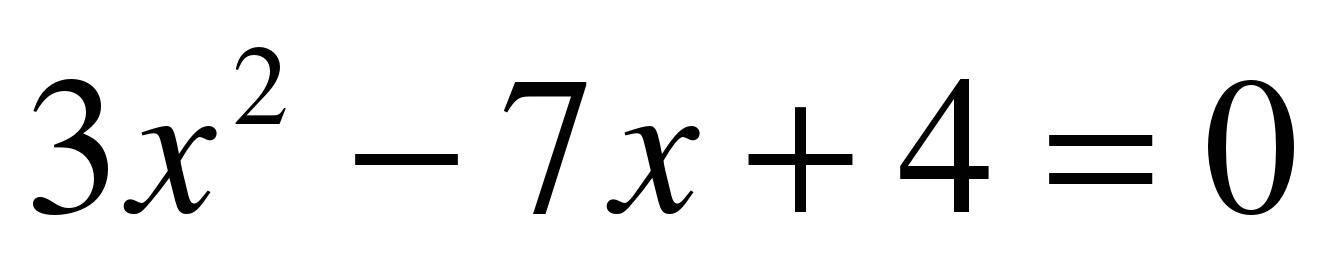. D =...

II ВАРИАНТ

1. Если 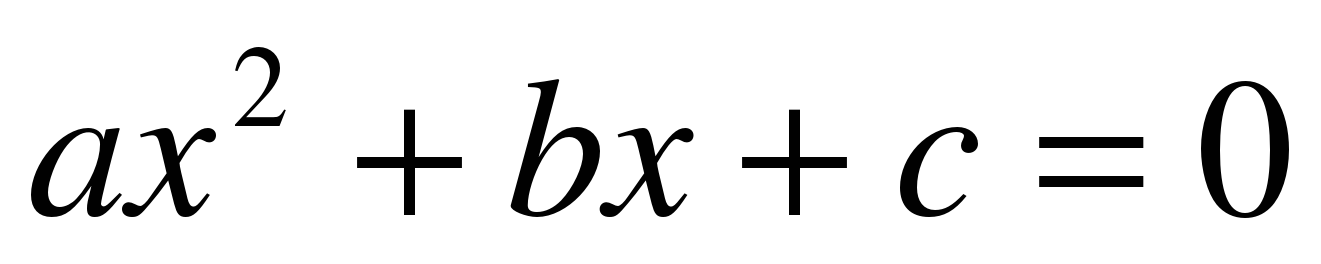квадратное уравнение, то a... коэффициент, с...

2. Уравнение x² = a, где a

3. Полное квадратное уравнение имеет единственный корень, если ...

4. Уравнение вида ax² + c = 0, где a 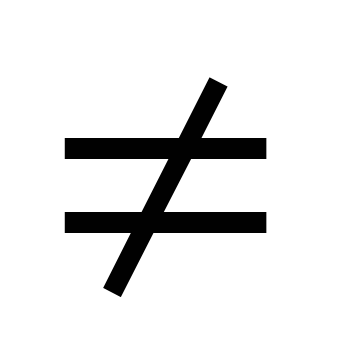0, c 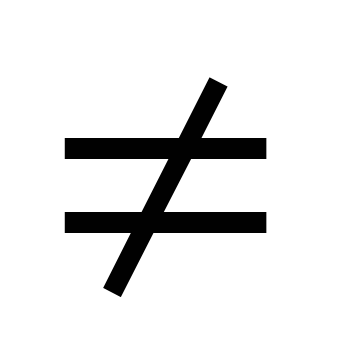0, называют ... квадратным уравнением.

5. Дано уравнение x²- 6x + 8 = 0. D =...

Проводится взаимопроверка. Ответы показываем через интерактивную доску.

4. Работа в парах

 Вернемся к эпиграфу нашего урока. Попытаемся сделать математику хотя бы сегодня на уроке немного более занимательной.

Вам необходимо угадать, что же находится в черном ящике.

Математика и биология

Учитель: Угадайте, что в ящике. Даю три определения этому предмету:

1. Непроизводная основа слова.

2. Число, которое после постановки его в уравнение обращает уравнение в тождество.

3. Один из основных органов растений.

/Корень/

Учитель: Вы должны определить, какого растения это корень, решив следующие уравнения в парах.

1. x²- 8x + 15 = 0

2. x² - 11x + 18 = 0

3. x² - 5x - 6 = 0

4. x² - 4x + 4 = 0

5. 3x² + 4x + 20 = 0

6. 5x²- 3x - 2 = 0

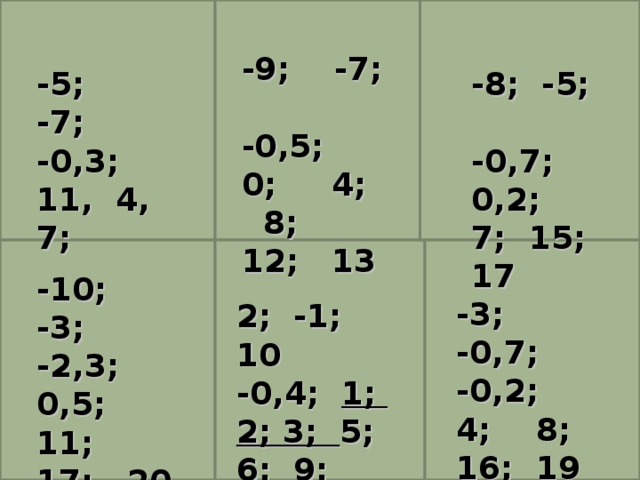
Учитель: Игра "Математическое лото". Найдите полученный ответ на экране. Проверить результат. Если ученики получают правильный ответ, то получат изображение розы, иначе – слайд с текстом «Проверьте решение».

Учитель: Что это за растение?

Посмотрите - у ограды
Расцвела царица сада.
Не тюльпан и не мимоза,
А в шипах красотка...

Лик пахучий,
А хвост колючий.

Яркие, пахучие -
Ай-ай-ай! Колючие!

Ответ: Роза.

Учитель: Значит, в черном ящике лежал корень розы, о которой в народе говорят: "Цветы ангельские, а когти дьявольские". О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.

 Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Мы увидели, что слово "корень" встречается на уроках биологии и математики. И не только.

1. Немного истории.

По словам математика Лейбница, "кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет".

Ученик заранее готовит сообщение об истории квадратных уравнений, с презентацией.

Кстати, а вы знаете, когда появились первые квадратные уравнения?

Очень давно. Их решали в Вавилоне около 2000 лет до нашей эры, а Европа три года назад отпраздновала 813 летие квадратных уравнений, потому что именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.

История математики уходит своими корнями в древние времена. Задачи, связанные с квадратными  уравнениями решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.

Испанский математик Вальмес в 1486 году как-то в семейном кругу обмолвился о том, что нашел формулу для решения уравнения четвертой степени. В числе гостей оказался влиятельный инквизитор. Услышав слова Вальмеса, он заявил, что волей Божьей решать эти уравнения человеку не дано, а найти формулу можно было только с помощью дьявола.

В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.

В древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто представлялись в стихотворной форме.

 6. Продвинутые способы решения квадратных уравнений

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.

В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. В математической науке есть десять способов решения квадратных уравнений.

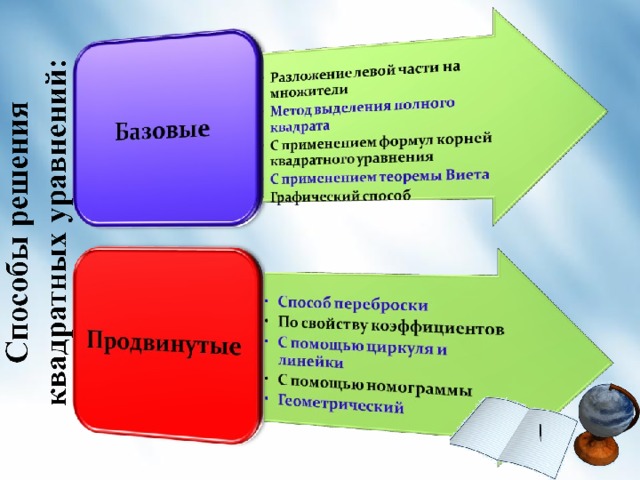
Способы решения квадратных уравнений, изучаемые в школе:

• Разложение левой части на множители

• Метод выделения полного квадрата

• С применением формул корней квадратного уравнения

• С применением теоремы Виета

• Графический способ

Продвинутые способы решения квадратных уравнений:

• Способ переброски

• По свойству коэффициентов

• С помощью циркуля и линейки

• С помощью номограммы

• Геометрический

Сегодня на уроке мы познакомимся с новым способом решения квадратных уравнений, который не изучается в школе. Но он очень интересный и вовсе не сложный.

Решим уравнение 2х² – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у² – 11у + 30 = 0.

Согласно теореме Виета

у₁ = 5 х₁ = 5/2 x₁ = 2,5

у₂ = 6 x₂ = 6/2 x₂ = 3.

Ответ: 2,5; 3.

Пример:

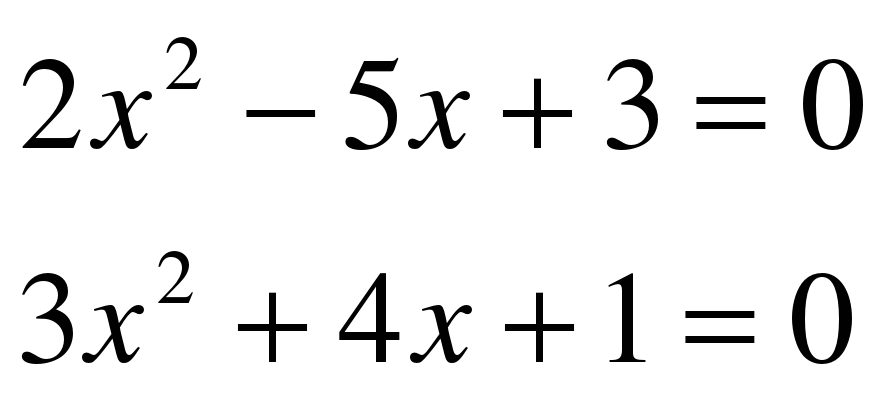
Решите самостоятельно:

1 вариант: 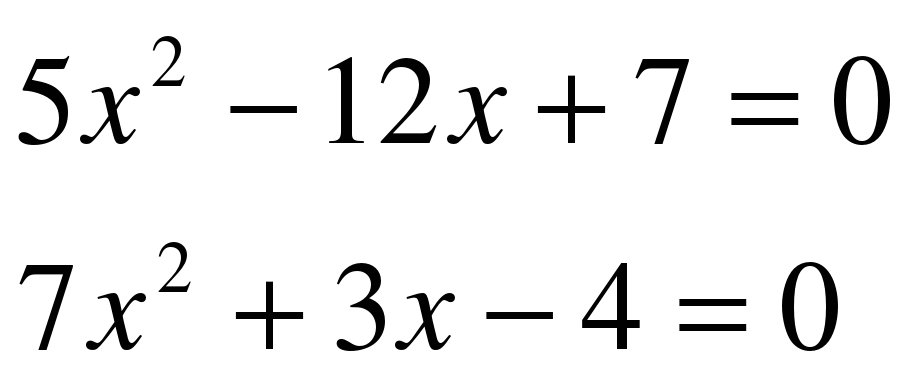2 вариант: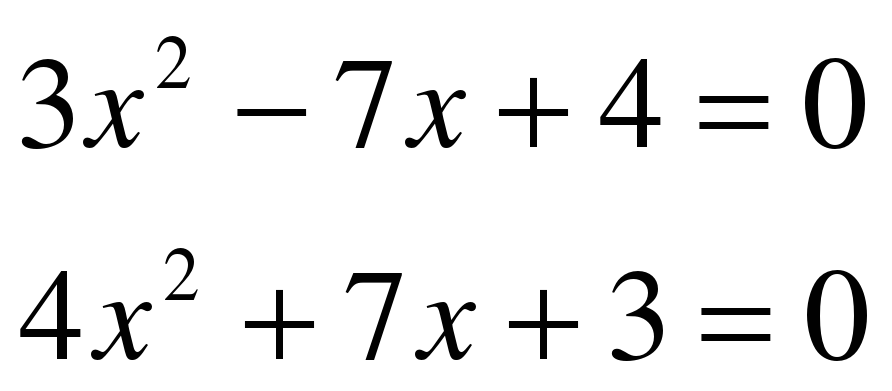

ЦОР №1289 на сайте e.edu.kz

узнайте достопримечательность

7. Викторина. "Дальше, дальше..."

В течение одной минуты ребята отвечают на вопросы, приведенные ниже:

1. Уравнение второй степени.

2. Сколько корней имеет квадратное уравнение, если D больше 0?

3. Равенство с переменной?

4. От чего зависит количество корней квадратного уравнения?

5. Как называется квадратное уравнение, у которого первый коэффициент - 1?

6. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?

7. Что значит решить уравнение?

8. Есть у любого слова, у растения и может быть у уравнения?

7. Итог урока.

Учитель:

Что нового мы узнали на уроке?

Какое уравнение называется квадратным?

Какие виды квадратных уравнений вы знаете?

И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

Оценивание учащихся. Сообщение домашнего задания.

Квадратные уравнения.

"Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".

Паскаль

Тест

«Квадратные уравнения»

Показать ответ

Показать ответ

Ответы к тесту:

1 вариант :

1) квадратным уравнением

2) отрицательный

3) приведенным квадратным уравнением

4) положительное число

5) 1

2 вариант:

1) первый коэффициент, свободный член

2) не имеет корней

3) равно нулю

4) неполным

5) 4

Угадайте, что в черном ящике?

Определения этому предмету:

• Непроизводная основа слова.

• Число, которое после

подстановки его в уравнение обращает уравнение в тождество.

• Один из основных органов растений.

1. x²- 8x + 15 = 0

2. x² - 11x + 18 = 0

3. x² - 5x - 6 = 0

4. x² - 4x + 4 = 0

5. 3x² + 4x + 20 = 0

6. 5x²- 3x - 2 = 0

-9; -7; -0,5; 0; 4; 8;

12; 13

-5; -7; -0,3;

11, 4, 7;

-8; -5; -0,7; 0,2; 7; 15; 17

-10; -3; -2,3; 0,5; 11; 17; 20

-3; -0,7; -0,2; 4; 8; 16; 19

2; -1; 10

-0,4; 1; 2; 3; 5; 6; 9;

Проверьте решение!

Древняя Индия

Задачи на квадратные уравнения встречаются уже в 499 г. В Древней Индии были распространены публичные соревнования в решении трудных задач.

Вывод формулы решения квадратного уравнения  в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.  

Решение квадратных уравнений способом «переброски».

Решим уравнение 2х 2  – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2  – 11у + 30 = 0.

Согласно теореме Виета

у 1  = 5 х 1  = 5/2 x 1  = 2,5

у 2  = 6 x 2  = 6/2 x 2  = 3.

Ответ: 2,5; 3.

Викторина. "Дальше, дальше..."

1. Уравнение второй степени.

2. Сколько корней имеет квадратное уравнение, если D больше 0?

3. Равенство с переменной?

4. От чего зависит количество корней квадратного уравнения?

5. Как называется квадратное уравнение, у которого первый коэффициент равен 1?

6. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?

7. Что значит решить уравнение?

8. Есть у любого слова, у растения и может быть у уравнения?

Вывод:

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

У. Сойер

Спасибо

за урок!