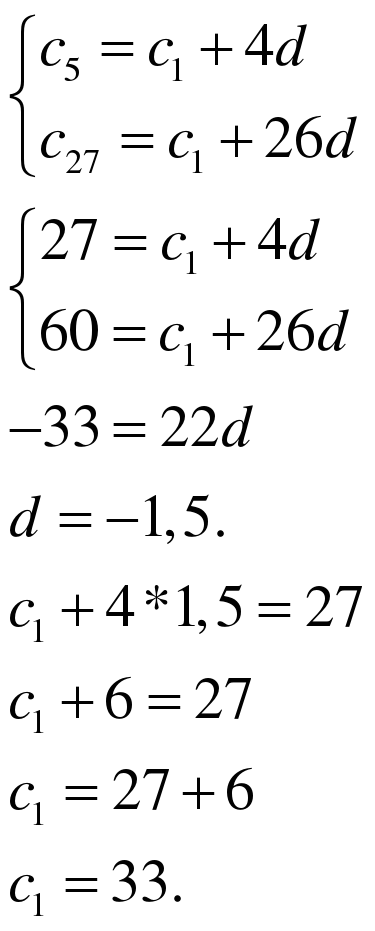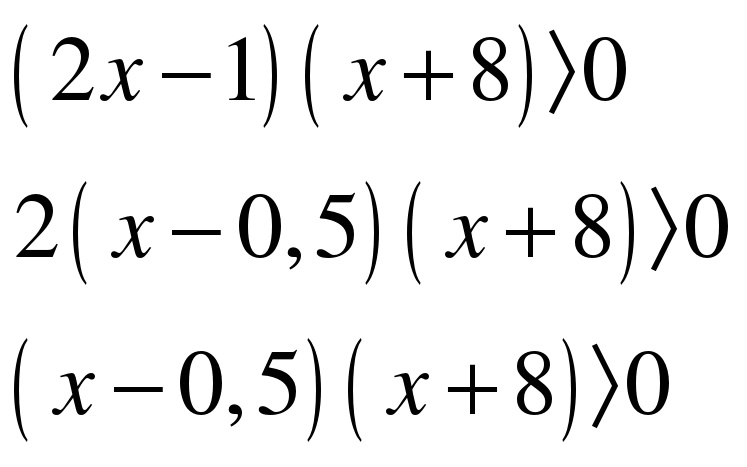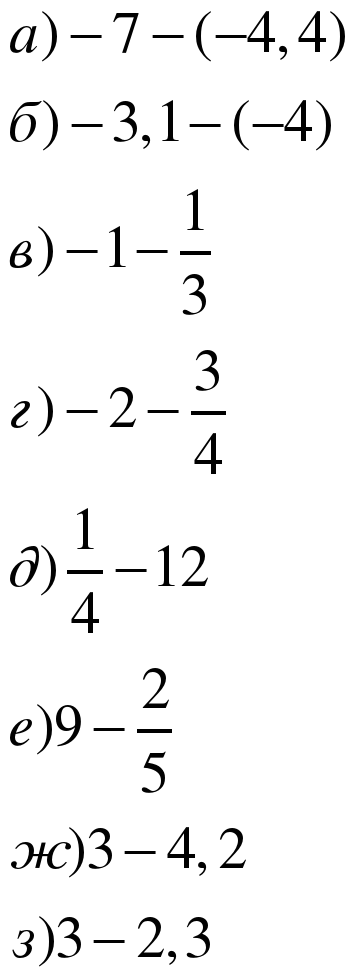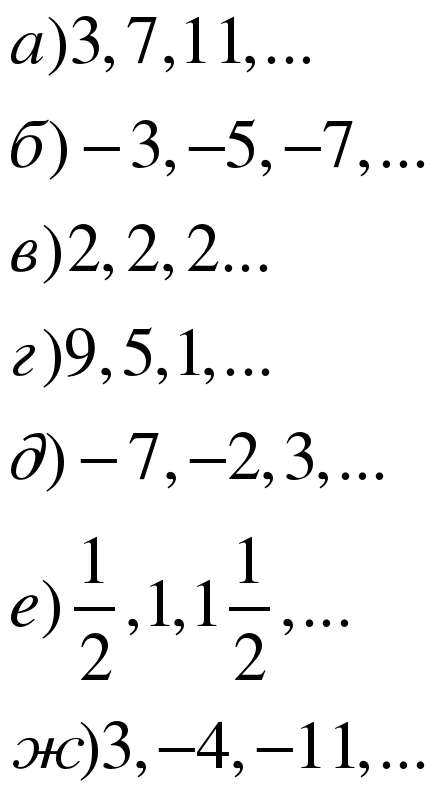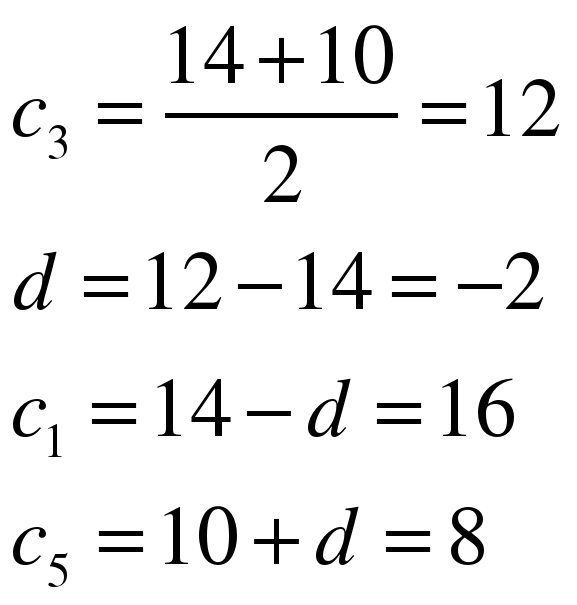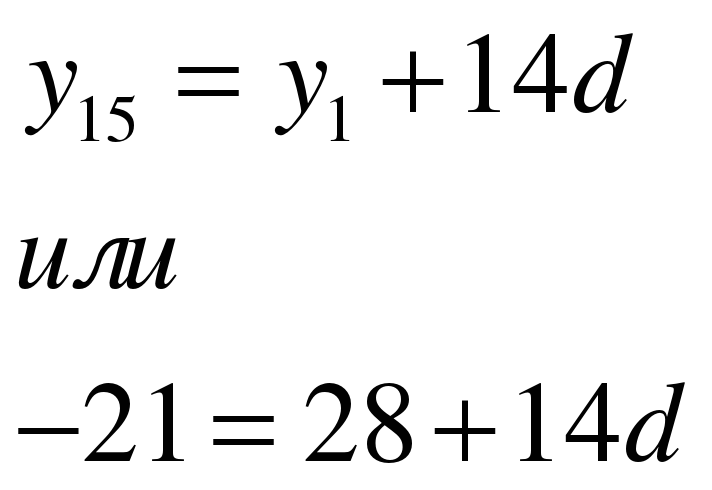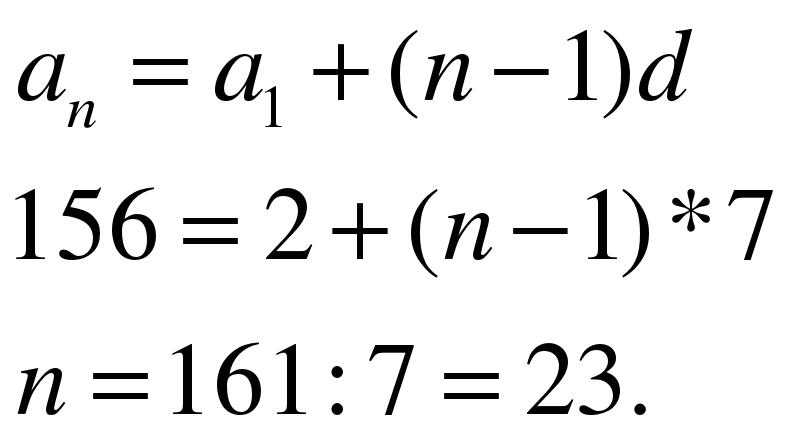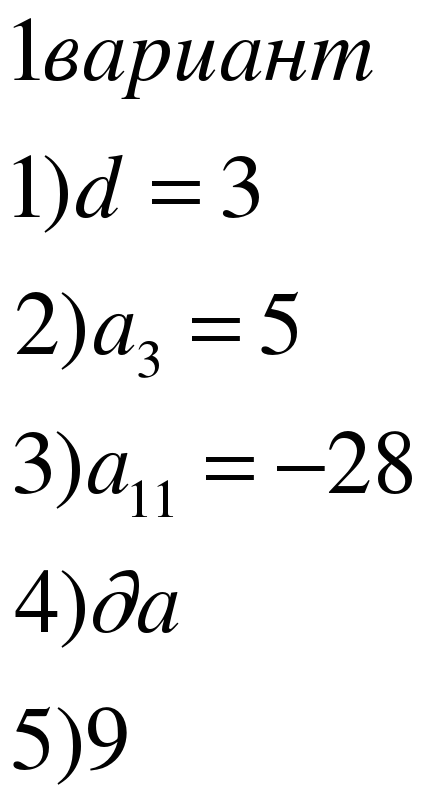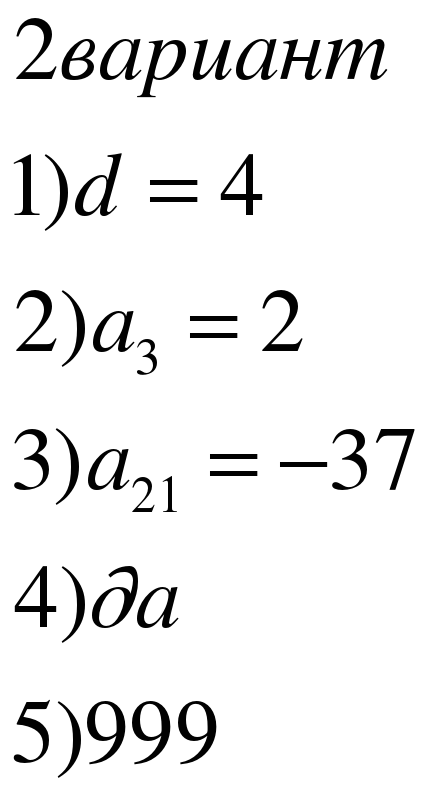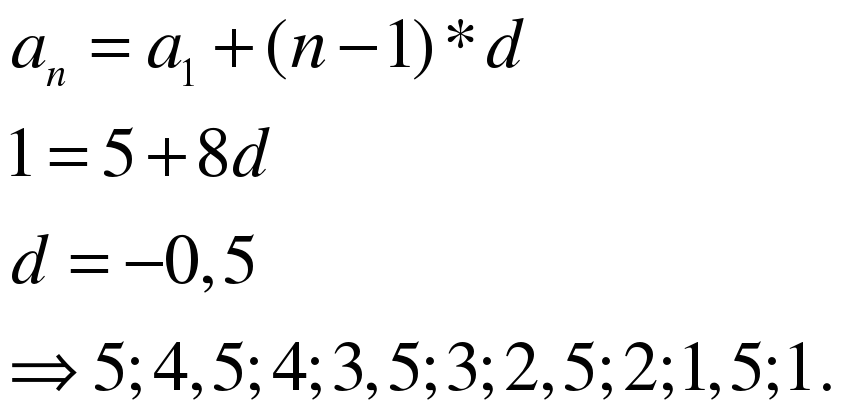Конспект урока с презентацией "Арифметическая прогрессия. Формула n-ого члена арифметической прогрессии"

Автор: Сватковская Елена Александровна,

учитель математики,

МБНОУ «Лицей № 3 (искусств)»

Арифметическая прогрессия.
Формула n-го члена арифметической прогрессии. (СЛАЙД 1)

Цели урока:

• Образовательная: повторение материала по темам «Числовая последова-

тельность»,

«Арифметическая прогрессия», «Формула n-го члена арифмети-

ческой прогрессии»; применение формул;

• Воспитательная: воспитание чувства коллективизма, личной ответственности,

перед товарищами по команде;

• Развивающая: развитие памяти, любознательности, активности.

Оборудование:

Компьютер, диапроектор, копировальная бумага, карточки для устного счета, обучающие карточки, ведомость соревнований, карточки для дидактической игры «Получи пятерку».

Тип урока: урок – соревнование.

ХОД УРОКА:

1. Организационный момент

Сегодня мы проведем урок – соревнование между командами (рядами). Также будет работать жюри. Все члены команды – победительницы получат «5». Победители в личном первенстве также получат «5». Отвечает тот, кто первым поднимет руку.

1. Повторение

(СЛАЙД 2)

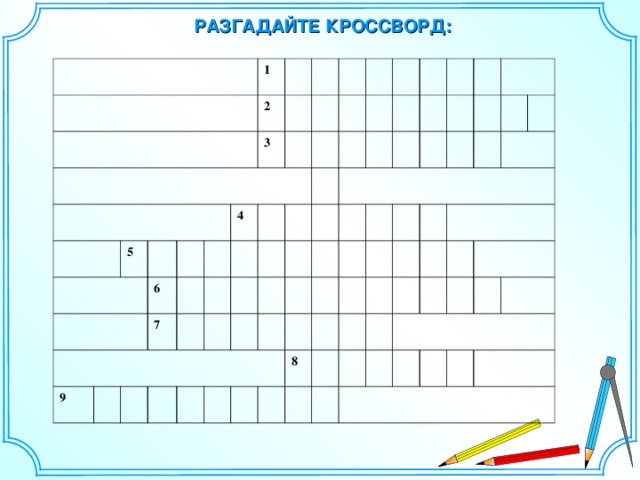
Вам предстоит разгадать кроссворд. За каждый верный ответ – один балл. В клетке с цифрой букву не писать, ответы давать в именительном падеже.

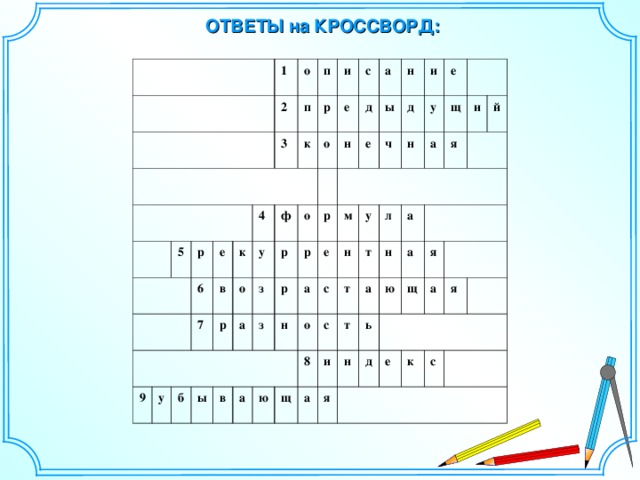
(Кроссворд проецируется на экран, вопросы читает учитель. Каждый ряд отгадывает его, ответы сдаются жюри. Затем все вместе проверяем ответы, которые также проецируются на экран) (СЛАЙД 3)

									1
									2
									3
							4
		5
				6
				7
										8
9

Вопросы:

1. Один из способов задания последовательности. (Описание)

2. Член последовательности, стоящий перед любым ее членом, начиная со второго. (Предыдущий)

3. Последовательность, в которой конечное число членов. (Конечная)

4. Закончите предложение: «N-ый член арифметической прогрессии задается с помощью….. . (Формула)

5. Название этой формулы с латинского означает «возвращаться». (Рекуррентная)

6. Последовательность, в которой каждый следующий член больше предыдущего. (Возрастающая)

7. Число, показывающее, на сколько любой член арифметической прогрессии меньше или больше предыдущего. (Разность)

8. Число, указывающего порядковый номер любого члена последовательности. (Индекс)

9. Последовательность, в которой каждый последующий член меньше предыдущего. (Убывающая)

Теперь повторим тему «Арифметическая прогрессия».

Внимание на экран. Найдите ошибки, допущенные в решении, и объясните их. За полный ответ вы получаете 2 балла. (СЛАЙД 4-5)

Задание 1 Найдите первый член и разность арифметической прогрессии 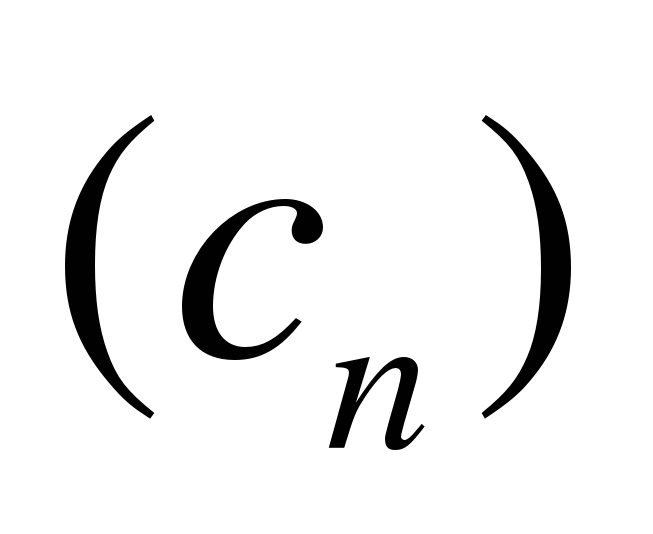, если .

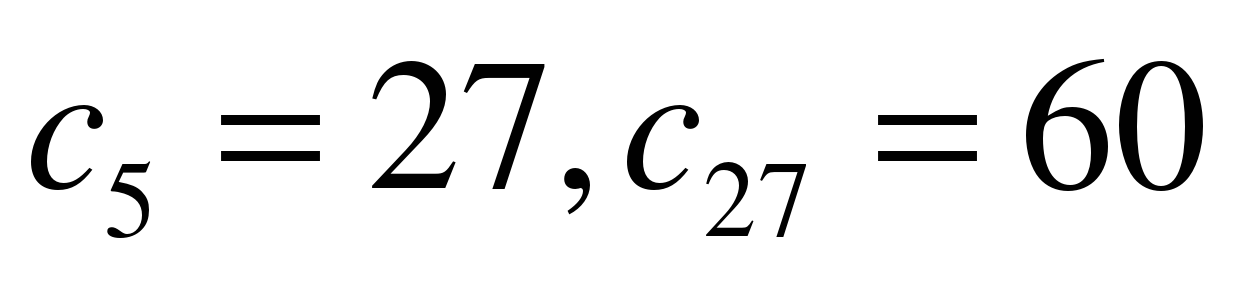РЕШЕНИЕ:

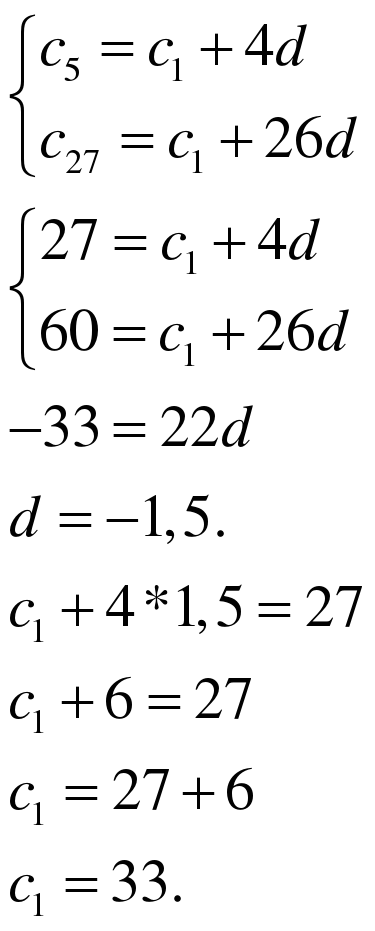
ОШИБКИ: 1) при вычитании 4d-26d потерян «-«, в результате неверно

найдено d;

2) при переносе слагаемого 6 в выражении 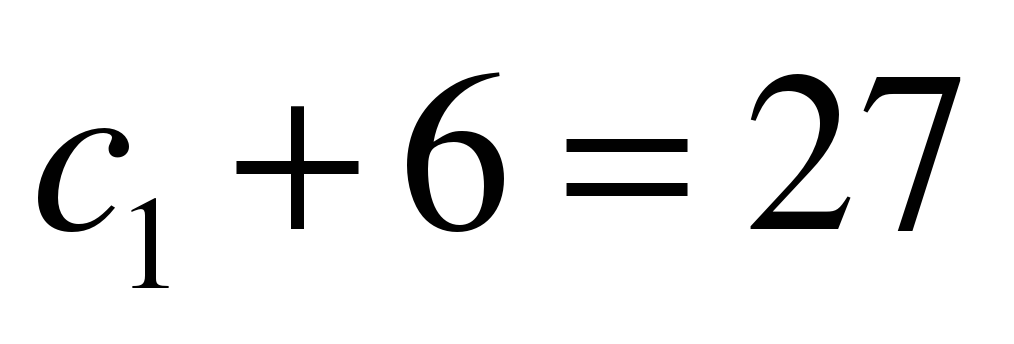потерян

«-«.

ВЕРНЫЙ ОТВЕТ: .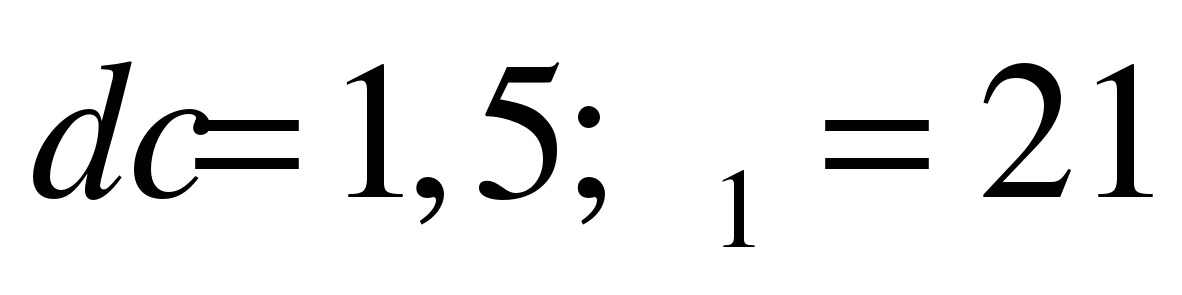

Задание 2 Решите неравенство (задание на повторение метода интервалов):

.

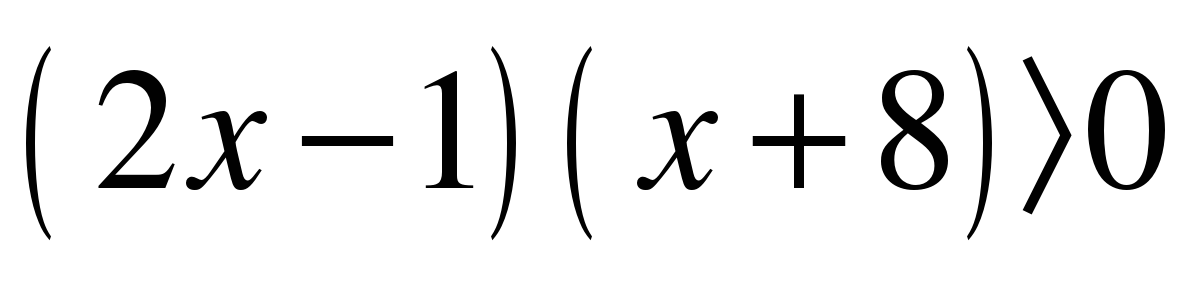РЕШЕНИЕ:

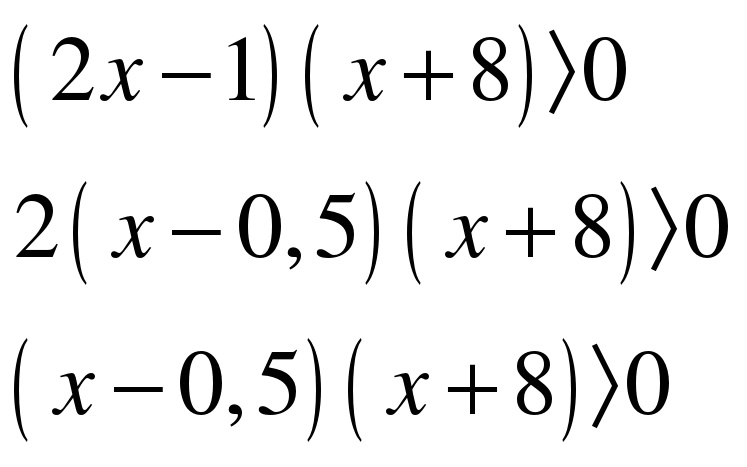
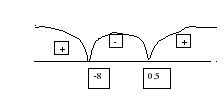
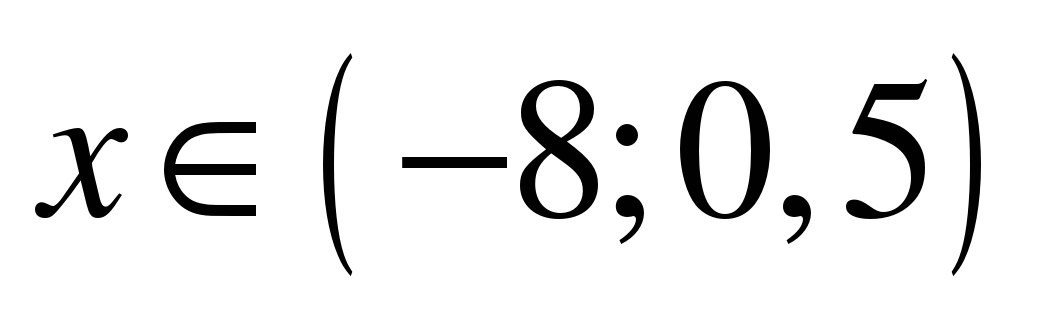
ОШИБКИ: в ответе неверно указаны промежутки. Знак неравенства 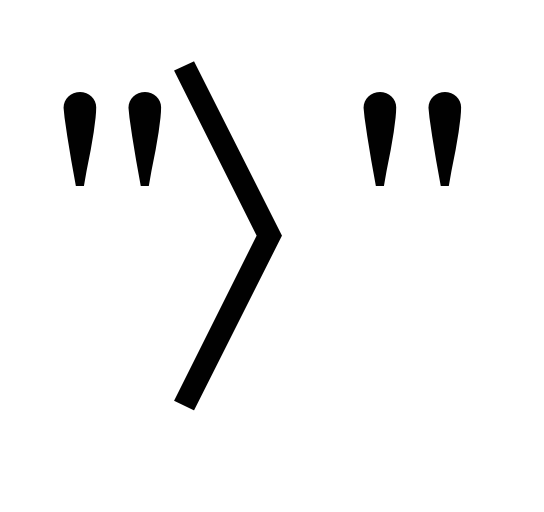, значит, ВЕРНЫЙ ОТВЕТ: .

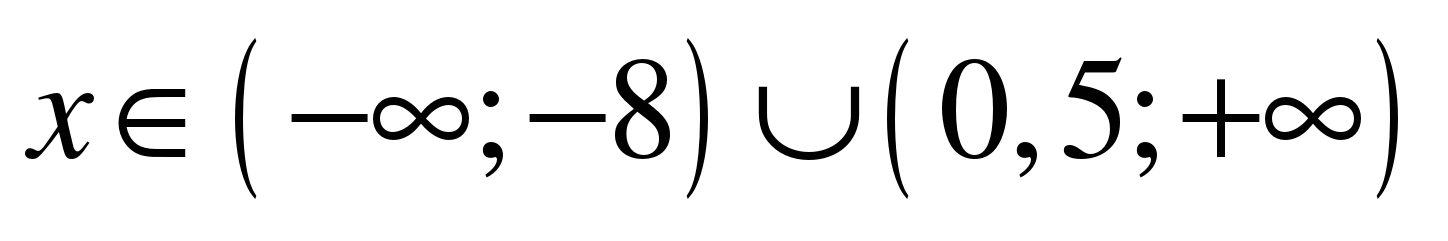1. Устный счет

(Пока весь класс работает устно, одновременно несколько человек из каждой команды работают по карточкам. Решения сдаются членам жюри. За каждый верный ответ – 3 балла).

Карточка 1

1. Найдите 16-ый член арифметической прогрессии - 5; - 2,5;…

2. Найдите разность арифметической прогрессии 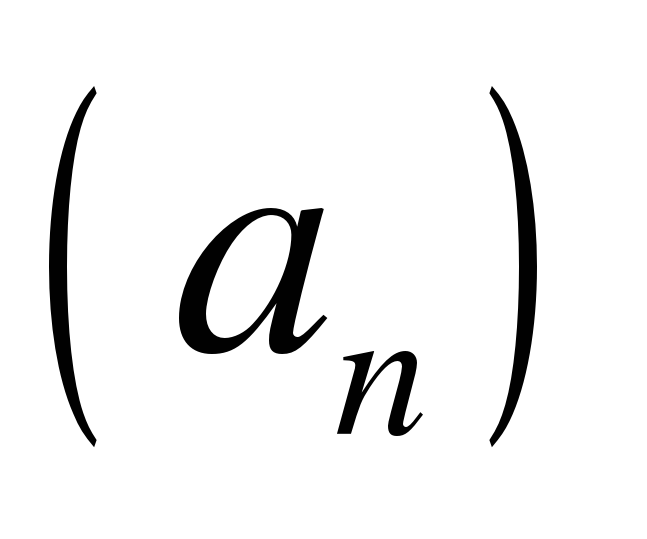, в которой .

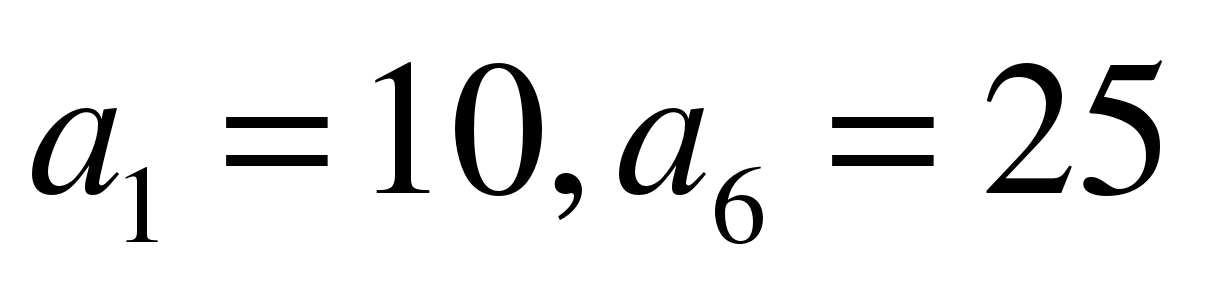Карточка 2

1. Запишите формулу n-го члена арифметической прогрессии 1, 4, 7, 10…

2. Является ли число 19 членом арифметической прогрессии, где ?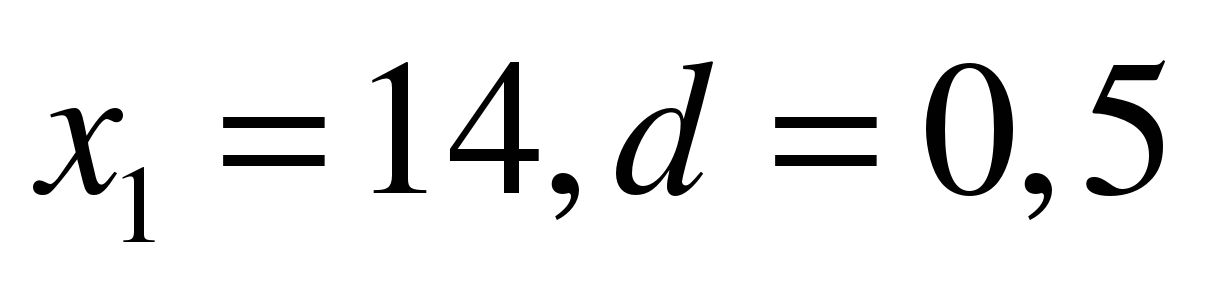

Карточка 3

1. При каких n члены арифметической прогрессии 15, 13, 11, отрицательны?

2. В арифметической прогрессии 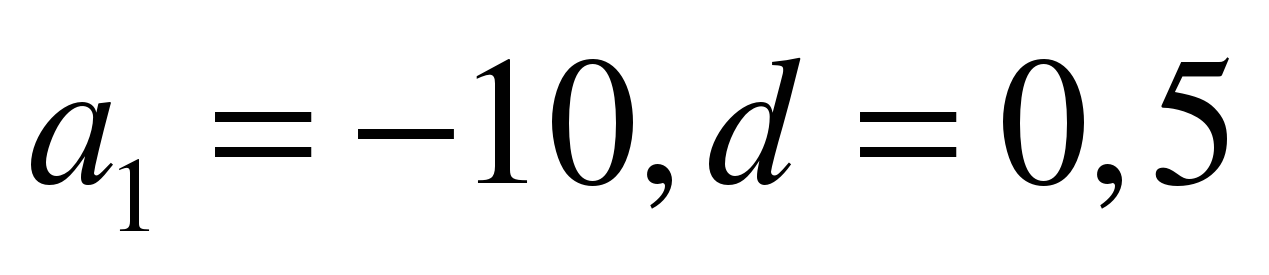. При каких n выполняется неравенство ?

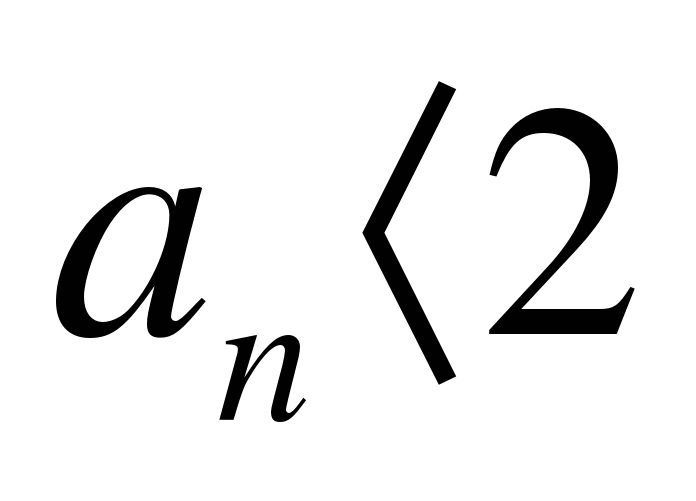(Остальные учащиеся работают над примерами, выведенными на экран.)

Задание 1 Вычислите: ( СЛАЙД 6)

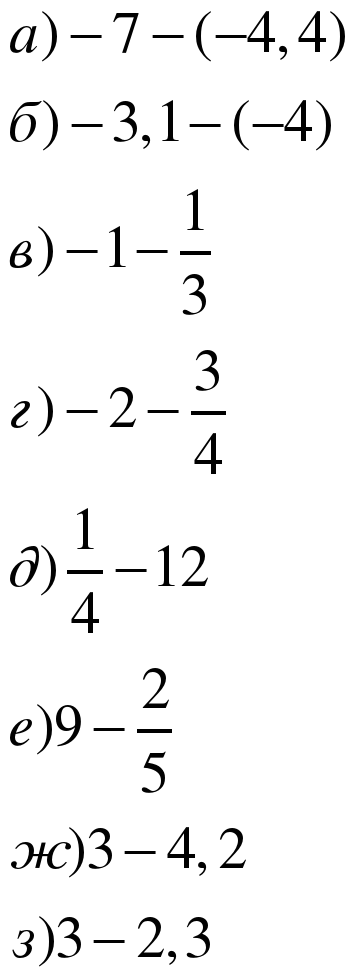
Задание 2 Найдите разность арифметической прогрессии: (СЛАЙД 7)

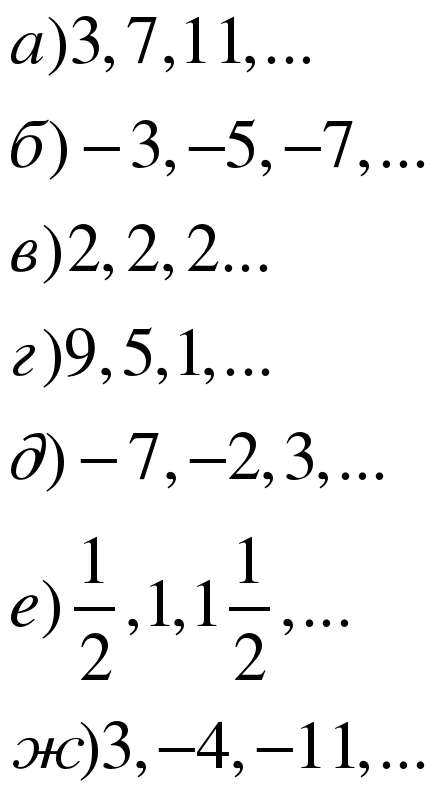
Задание 3 Найдите неизвестные члены арифметической прогрессии:

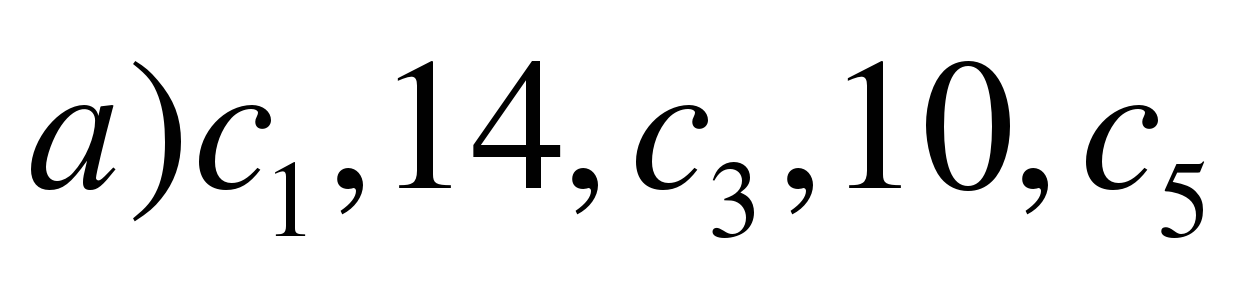(СЛАЙД 8)

РЕШЕНИЕ:

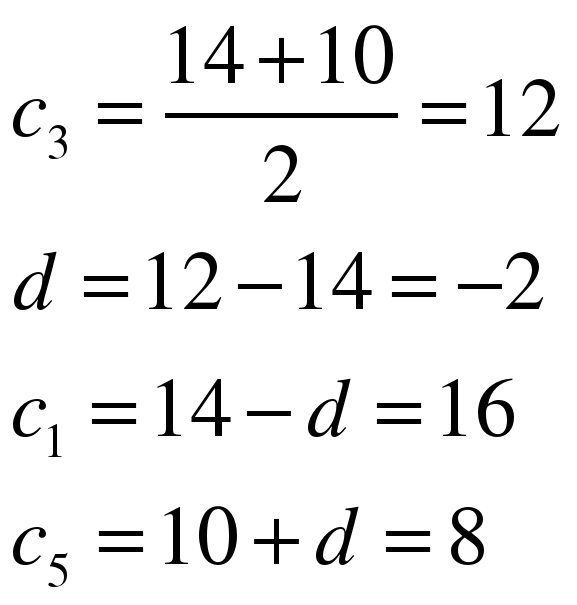
ОТВЕТ: 16, 14, 12, 10, 8.

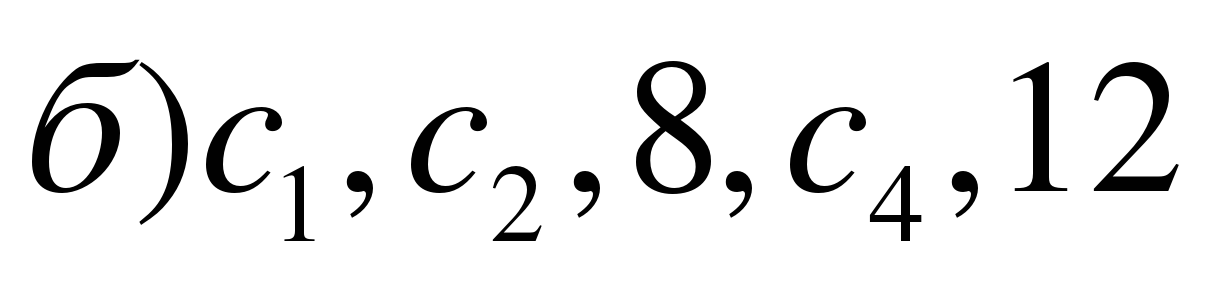
РЕШЕНИЕ:

ОТВЕТ: 4, 6, 8, 10, 12.

4.Теоретическая разминка

(Учащиеся 1 ряда задают вопросы учащимся 2 и 3 рядов. Учащиеся 2 рада – учащимся 1 и 3 рядов, в 3 ряда – учащимся 1 и 2 рядов.
За предложенный вопрос учащиеся получают 1 балл, за правильный ответ – 2 балла. Выигрывает та команда, которая задаст больше вопросов за 1 минуту.)

5.Лучший комментатор

(Учащийся комментирует ход решения с места, делая записи в тетради. Учитель и класс оценивают комментирование. Побеждает тот, кто лучше и полнее прокомментирует решение. За полный, подробный комментарий команда получает 3 балла.)

Задание 4 Разность арифметической прогрессии равна 4. Найдите первый ее член, если десятый равен 128. (СЛАЙД 9)

РЕШЕНИЕ:

По формуле общего члена имеем:

.

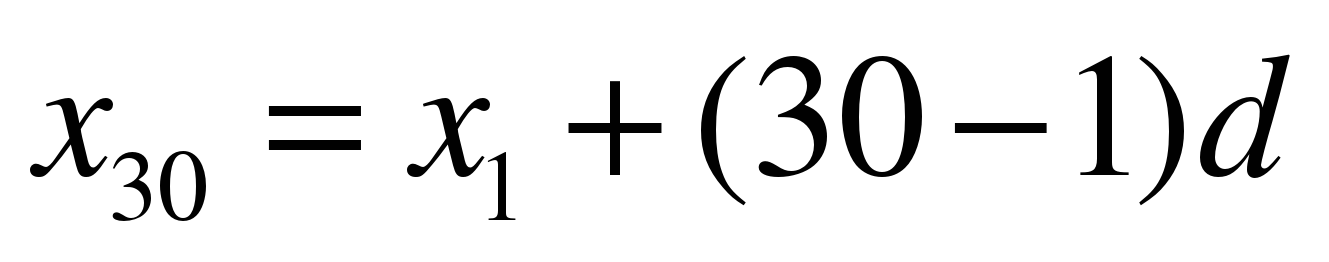Отсюда

.

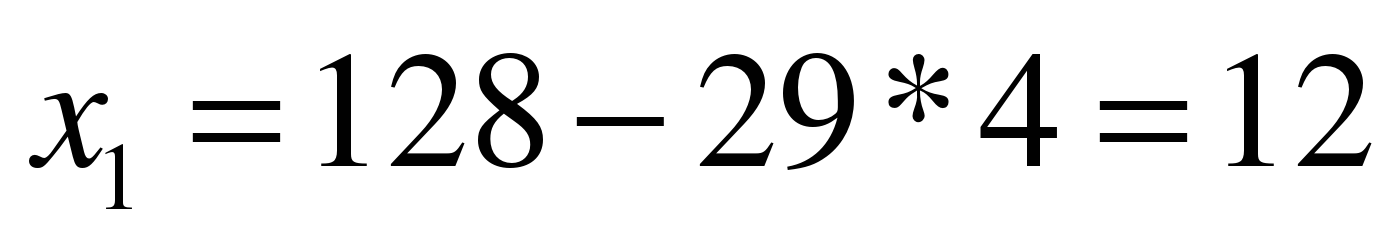Задание 5 Найдите разность арифметической прогрессии, если ее первый член равен 28, а пятнадцатый равен – 21. (СЛАЙД 10)

РЕШЕНИЕ:

По формуле общего члена имеем:

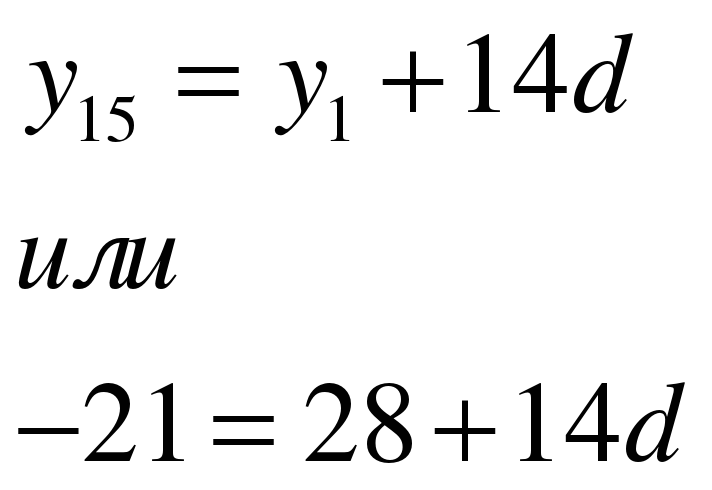
Отсюда

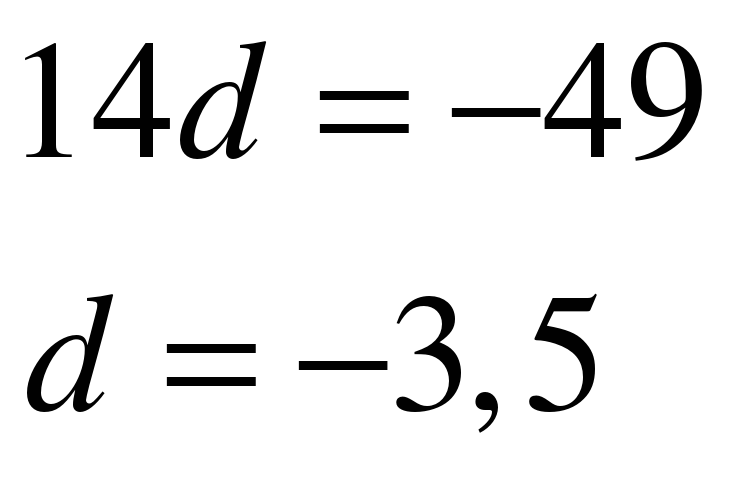
Задание 6 Число 156 является членом арифметической прогрессии 2, 9,…

Найдите номер этого члена. (СЛАЙД 11)

РЕШЕНИЕ:

Находим разность:

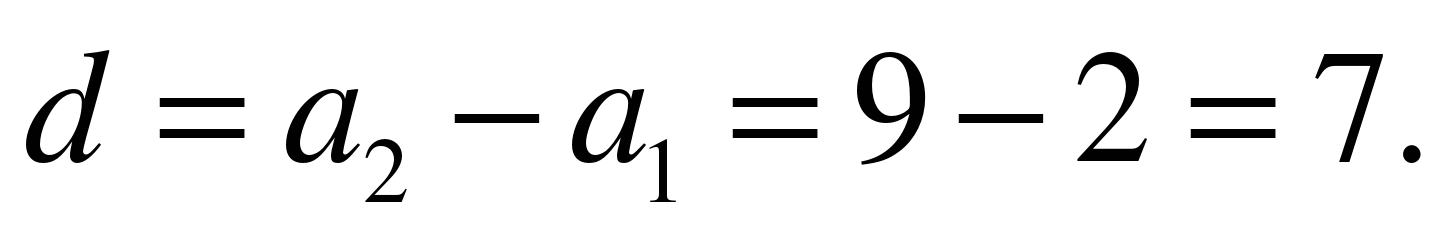
По формуле общего члена имеем:

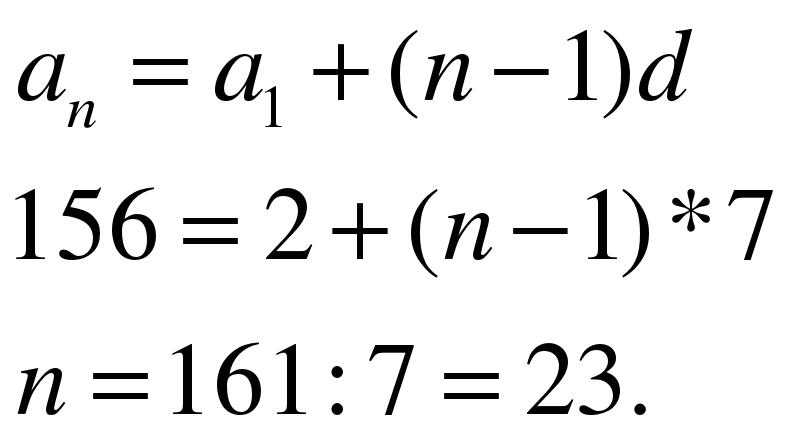
6.Прогрессия в физике

(Задания выполняются самостоятельно с последующей проверкой на экране). (СЛАЙД 12)

Задание 7 Свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду – на 9,8 м больше, чем в предыдущую. Какое расстояние будет пройдено падающим телом за 8-ую секунду?

РЕШЕНИЕ:

По формуле общего члена имеем:

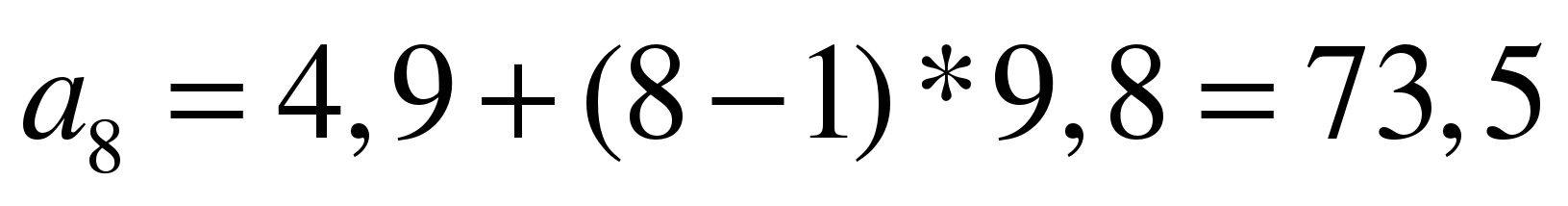
ОТВЕТ: значит, за 8-ую секунду тело пройдет 73,5 м.

7. Слушайте и запоминайте.

(Математический диктант. Читает учитель. Учащиеся пишут его в двух экземплярах (под копирку), копии сдают, а в тетрадях выполняют самопроверку со слайдом с ответами и выставляют себе оценку. Если оценка учителя и самооценка совпадут, то команде все оценки за диктант «5», «4» и «3» засчитываются в виде баллов. Если в диктанте допущена 1 ошибка, ставится «4», 2 ошибки – «3», 3 ошибки – «2».)

ДИКТАНТ (в скобках задание 2 варианту)

1. В арифметической прогрессии первый член равен 5 (3), второй 8 (7).

Найдите разность.

1. В арифметической прогрессии первый член равен 9 (10), второй 7 (6).

Найдите третий член.

1. Найдите одиннадцатый (двадцать первый) член арифметической

прогрессии, если ее первый член равен 2 (3), а разность -3 (-2).

1. Является ли последовательность положительных четных (нечетных)

чисел, записанных в порядке возрастания, арифметической

прогрессией?

1. Запишите последний член последовательности всех однозначных

(трехзначных) чисел, записанных в порядке возрастания.

ОТВЕТЫ: (СЛАЙД 13)

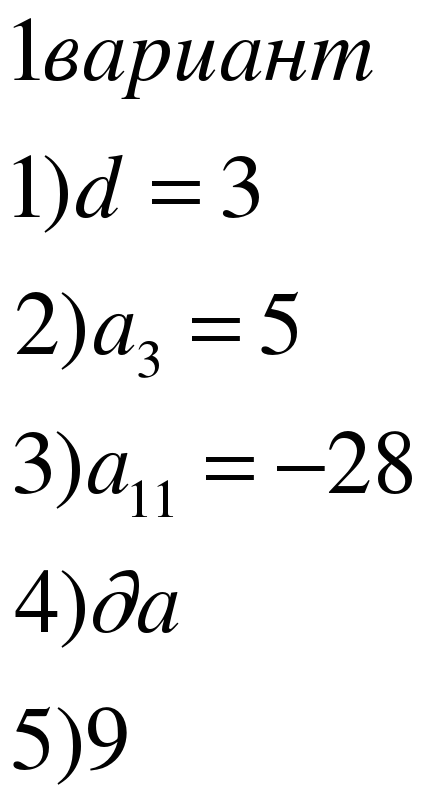
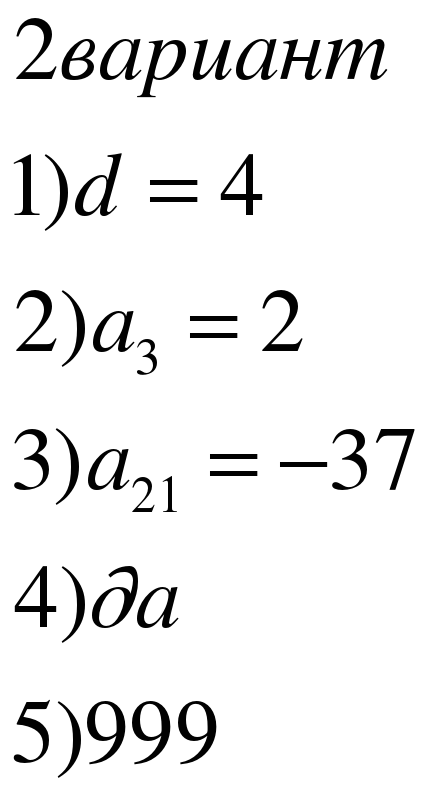
8. Задача на смекалку. (СЛАЙД 14-15)

5 баллов получит та команда, которая быстрее предложит верный способ решения:

В арифметической прогрессии первый член равен 5, девятый член равен 1.

Выпишите первые девять членов этой арифметической прогрессии.

РЕШЕНИЕ:

По формуле общего члена имеем:

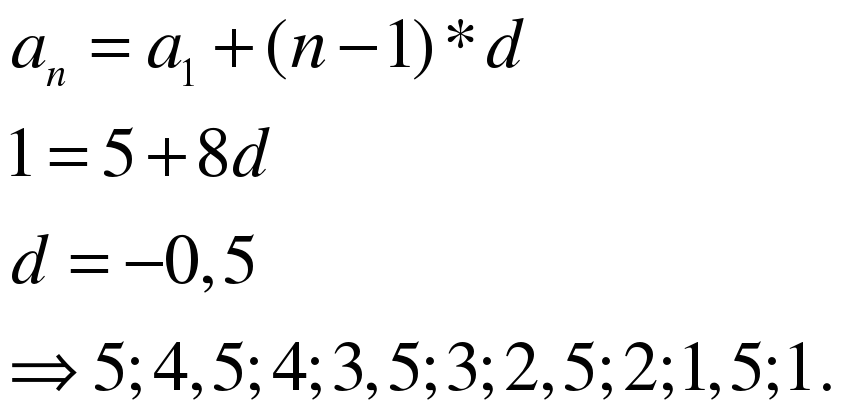
9.Дидактическая игра «ПОЛУЧИ ПЯТЕРКУ»

	а	b	c	d	e
1
2
3
4
5

Все вы любите получать пятерки. Сейчас вам представится возможность мгновенно получить «5», для этого нужно принять участие в игре.

Заполните таблицу, вписывая в каждую клетку знак «+» или «-«.

Будьте внимательны. Я буду читать некоторые утверждения. Если вы согласны, то пишите «+», если нет, то «-«.

1а. Последовательность, у которой конечное число членов, называется

конечной. +

1b. Последовательность, у которой бесконечное число членов, называется

бесконечной. +

1с. Арифметическая прогрессия – это последовательность. +

1d. У возрастающей последовательности второй член меньше первого. –

1е. У убывающей последовательности второй член больше первого. –

2а. В арифметической прогрессии каждый член, начиная со второго, равен

предыдущему, сложенному с одним и тем же числом. +

2b. Последовательность нельзя задать описанием. –

2с. В арифметической прогрессии каждый член, начиная со второго, равен

предыдущему, сложенному с различными числами. –

2d. Последовательность не бывает убывающей. –

2е. Никакая последовательность не может быть задана рекуррентной

формулой. –

3а. n-ый член арифметической прогрессии задается с помощью

формулы. +

3b. Чтобы найти разность арифметической прогрессии, надо от любого

ее члена отнять предыдущий. +

3с. Чтобы найти любой член арифметической прогрессии, достаточно

знать ее первый член и разность. +

3d. Последовательность натуральных чисел, расположенных в порядке

возрастания, не является арифметической прогрессией. –

3е. Последовательность простых чисел является арифметической

прогрессией. –

4а. Чтобы найти n-ый член арифметической прогрессии, надо из

пятого ее члена вычесть первый. –

4b. Формула n-го члена арифметической прогрессии . –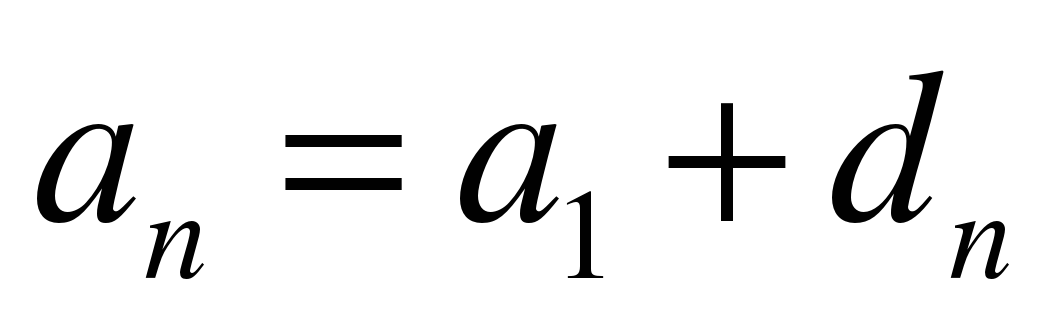

4с. Формула n-го члена арифметической прогрессии . +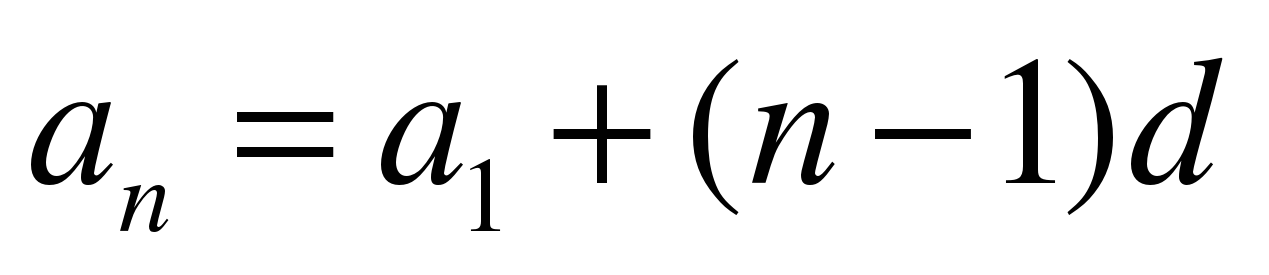

4d. Последовательность положительных четных чисел, расположенных

в порядке возрастания, не является арифметической прогрессией. –

4е. Чтобы найти n-ый член арифметической прогрессии, надо знать ее

любые два члена. –

5а. Последовательность положительных нечетных чисел, расположенных

в порядке возрастания, является арифметической прогрессией. +

5b. У возрастающей последовательности каждый следующий член больше

предыдущего. +

5с. У убывающей последовательности каждый следующий член меньше

предыдущего. +

5d. Для нахождения разности арифметической прогрессии надо знать ее

первый и последний члены. –

5е. Разность арифметической прогрессии обозначается . –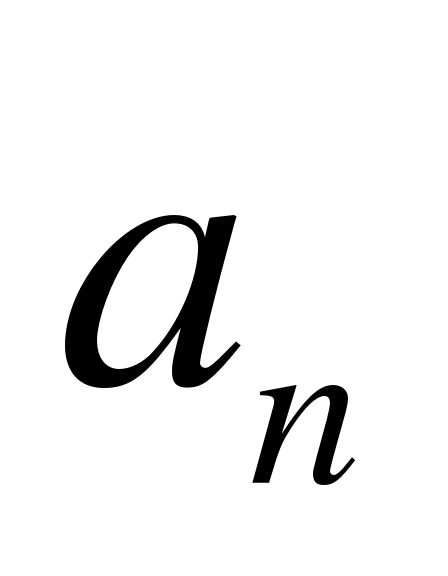

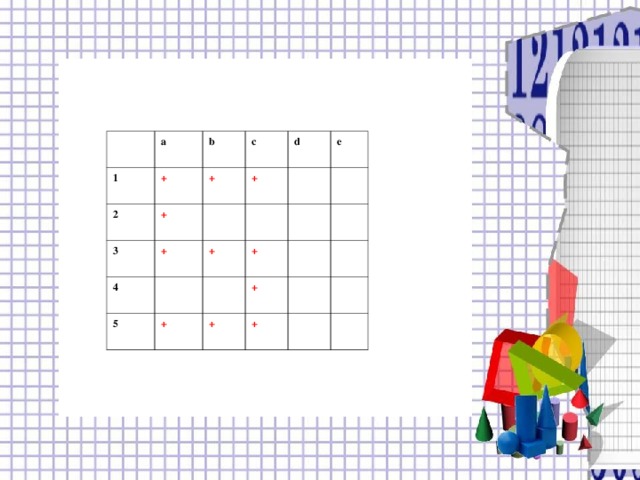
Соедините цветным карандашом все «+». Что у вас получилось?

(Верный ответ проектируется на экран) (СЛАЙД 16)

	а	b	c	d	e
1	+	+	+
2	+
3	+	+	+
4			+
5	+	+	+

10.Подведение итогов урока.

(Подведение итогов соревнования)

Личное первенство:

1 место……

2 место…..

3 место…..

Командное первенство:

1 место……

2 место…..

3 место…..

ЛИТЕРАТУРА:

1. Л.И. Мартышова «Открытые уроки алгебры и начала анализа»,

Москва. «ВАКО», 2012

1. Ш.А. Алимов, Ю.М. Колягин «Алгебра: учебник для 9 класса общеобразовательных учреждений», М.: Просвещение, 2006

1. Алгебра: сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс», М.: Дрофа, 1996

ТАБЛИЦА ПОДВЕДЕНИЯ ИТОГОВ

Для подведения итогов и выявление команды – победительницы можно использовать простую таблицу:

№	Этап урока	Команда 1	Команда 2	Команда 3
1	Повторение. Кроссворд.
2	Найдите ошибки.
3	Устный счет.
4	Теоретическая разминка.
5	Лучший комментатор.
6	Прогрессия в физике.
7	Слушайте и запоминайте (математический диктант) (оценка ученика)
8	Слушайте и запоминайте (математический диктант) (оценка учителя)
9	Задача на смекалку.
10	Дидактическая игра «Получи пятерку».
11	Работа по карточкам.
12	Дополнительное задание.
Итого

Следующая таблица позволяет определить не только командное первенство, но и личное:

Ф.И.О. учащегося

Кроссворд

Проверка д/з

Карточки

Устный счет

Теоретическая разминка

Лучший комментатор

Задача по физике

Матем. диктант (оценка учащегося)

Матем. диктант (оценка учителя)

Задача на смекалку

Получи пятерку

Дополнит. задание

Итоги

1 ряд

1. Иванов Иван

1

2

1 1 1

2. Петров Антон

1 1

1 2 1

3…..

2

2 2

4…..

1

5……

Кол-во баллов

4

4

2 рад

1.Сидоров Петр

2. Попова Анна

3……

Кол-во баллов

3 ряд

1. Мишин Олег

2…..

3…..

Кол-во баллов

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

Презентацию подготовила учитель математики МБНОУ «Лицей №3 (искусств)»

Сватковская Елена Александровна

РАЗГАДАЙТЕ КРОССВОРД:

1

5

2

9

3

6

4

7

8

ОТВЕТЫ на КРОССВОРД:

5

1

о

2

р

3

9

п

п

6

е

у

к

в

7

к

4

р

и

о

у

б

о

р

ф

с

е

ы

р

о

а

з

а

н

д

р

р

з

в

р

н

ы

е

а

н

е

а

и

м

д

ч

с

о

ю

у

у

е

н

н

с

щ

8

т

а

т

л

щ

и

а

а

а

я

н

т

и

я

а

н

ь

й

ю

д

я

щ

е

а

к

я

с

НАЙДИТЕ ОШИБКУ: Задание 1 Найдите первый член и разность арифметической прогрессии , если .

Решение:

НАЙДИТЕ ОШИБКУ: Задание 2 Решите неравенство (задание на повторение метода интервалов):

РЕШЕНИЕ:

-

+

+

-8

0,5

Вычислите:

Найдите разность арифметической прогрессии:

• а) 3, 7, 11,….
• б) -3, -5, -7,…
• в) 2, 2, 2,…
• г) 9, 5, 1,…
• д) -7, -2, 3,…
• е)1/2, 1, …
• ж) 3, -4, -11,…

Найдите неизвестные члены арифметической прогрессии:

• Разность арифметической прогрессии равна 4 . Найдите первый ее член, если десятый равен 128 .

• Найдите разность арифметической прогрессии, если ее первый член равен 28 , а пятнадцатый равен – 21 .

• Число 156 является членом арифметической прогрессии 2, 9,…

Найдите номер этого члена.

Свободно падающее тело

проходит в первую секунду 4,9 м, а в каждую

следующую секунду –

на 9,8 м больше, чем в

предыдущую.

Какое расстояние будет

пройдено телом за

8 -ую секунду?

ОТВЕТЫ К ДИКТАНТУ:

ЗАДАЧА НА СМЕКАЛКУ:

• В арифметической прогрессии первый член равен 5 , девятый член равен 1 .

Выпишите первые девять членов этой арифметической прогрессии.

Решение:

а

1

+

b

2

3

+

+

c

+

+

d

4

e

+

5

+

+

+

+

+

источник шаблона.

Автор данного шаблона:

Ермолаева Ирина Алексеевна

учитель информатики и математики

МОУ «Павловская сош»

с.Павловск

Алтайский край

Название сайта: http://pedsovet.su/

• http://www.globallab.ru/mim/mim/intro/all.2476.ru.htm
• http://dreaminginjavascript.wordpress.com/2008/07/15/javascript-numbers-can-bite/

http://www.myjulia.ru/data/cache/2009/07/17/152778_2266-0x600.jpg

http://files.botevcheta.webnode.com/200000016-45175461c2/1stationery15-med.jpg

http:// www.mathknowledge.com /images/custom/LOGO.GIF

http://www.ccboe.net/Teachers/Durham_Sharon/images/918F9422010B4BB0B160956D6B9D4E34.JPG

http://lake.k12.fl.us/cms/cwp/view.asp?A=3&Q=427619

http://www.533school.ru/nach.htm

Интернет-ресурсы

Циркуль: http://www.daviddarling.info/images/compasses.jpg

Карандаш: http://www.proshkolu.ru/content/media/pic/std/3000000/2240000/2239093-7acd9447b354cc7e.gif

Угольник-транспортир:

http://p.alejka.pl/i2/p_new/25/38/duza-ekierka-geometryczna-z-uchwytem-rotring-14-cm_0_b.jpg

Фон «тетрадная клетка»:

http://radikal.ua/data/upload/49112/4efc3/3bd0a3d6bb.jpg

Источник шаблона: Шумарина Вера Алексеевна,учитель ГКС(К)ОУ С(К)ОШ №11 VIII вида. г. Балашов Сайт: http :// pedsovet.su /

источник шаблона: Татарников Виталий Викторович учитель физики МОУ СОШ №20 п. Баранчинский, г. Кушва, Свердловской обл.

http://pedsovet.su/

источник шаблона:

Ранько Елена Алексеевна

учитель начальных классов

МАОУ лицей №21

г. Иваново

Сайт: http://pedsovet.su/

• источник шаблона: http://pedsovet.su/
• Автор: Макшина Ирина Юрьевна, учитель русского языка Специальной (коррекционной) школы № 657 (8 вида) Приморского района Санкт-Петербурга

• Фон - http://i.allday.ru/uploads/posts/2010-09/1285145016_shutterstock_55111003.jpg
• Фон - http://i.allday.ru/uploads/posts/2010-09/1285145016_shutterstock_55111003.jpg

Укажите источник шаблона: сайт http://pedsovet.su

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Савченко Елена Михайловна,

учитель математики высшей квалификационной категории.

Муниципальное общеобразовательное учреждение гимназия №1,

г. Полярные Зори, Мурманская обл.