Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока математики Та?ырыбы: Келтіру формулалары
О?ушылар сын т?р?ысынан ойлай отырып, с?йір б?рышты? тригонометриялы? функциясыны? ?рбір б?рышында?ы синустыы?, косинусты?, тангенсті?, котангенсті? келтіру формулаларымен танысады, осы формулаларды тригонометриялы? ?рнектерді т?рлендіруде ж?не есептерді шы?ару кезінде ме?гереді. Берілген тапсырмалар ар?ылы білімдерін толы?тырады.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока математики Та?ырыбы: Келтіру формулалары »
Полезное для учителя
Распродажа видеоуроков!
1800 руб.
3000 руб.
1720 руб.
2860 руб.
1690 руб.
2820 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
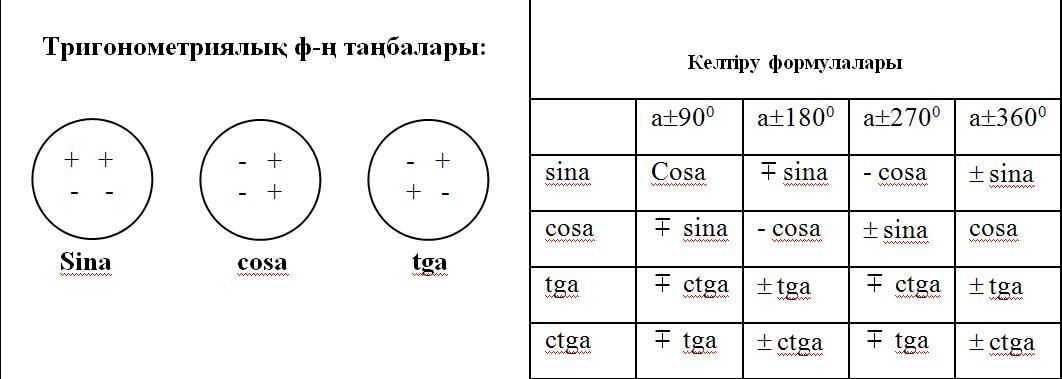

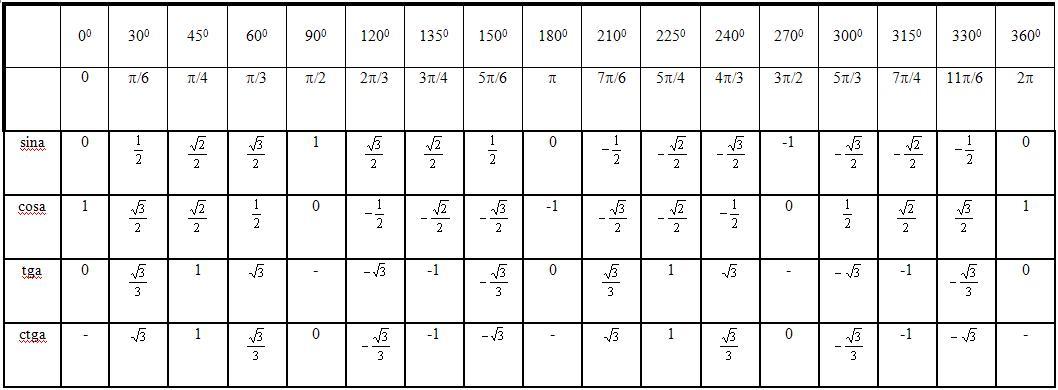

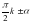 (мұндағы k- кез келген бүтін сан, α - сүйір бұрыш) бұрышының функциялары берілсе, онда оларды α-бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы. Ол үшін арнайы берілген келтіру формулалары қолданылады.
(мұндағы k- кез келген бүтін сан, α - сүйір бұрыш) бұрышының функциялары берілсе, онда оларды α-бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы. Ол үшін арнайы берілген келтіру формулалары қолданылады.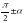 ;
; 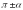 ;
; 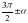 ;
; 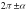 бұрыштарын қарастырамыз.
бұрыштарын қарастырамыз.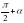 түріне келтіру болады ( мұндағы α -сүйір бұрыш). Шеңбер алайық.
түріне келтіру болады ( мұндағы α -сүйір бұрыш). Шеңбер алайық. 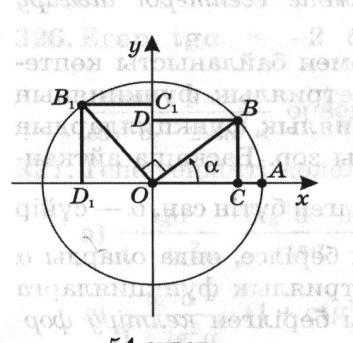
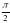 бұрышына бұру арқылы шықты. Расында
бұрышына бұру арқылы шықты. Расында  ВОВ1 =
ВОВ1 = 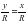 және
және 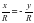
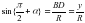 , sin α =
, sin α = 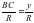 Дәл осылай cos
Дәл осылай cos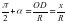 ,
,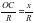
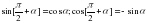 (1)
(1) 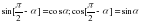 [2]
[2] 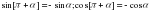 [3]
[3] 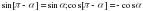 [4]
[4] 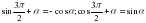 [5]
[5] 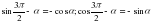 [6]
[6] 















