ТЕМА: ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ДЛЯ НАХОЖДЕНИЯ ПЛОЩАДЕЙ ФИГУР (2 ЧАСА)
Урок, на котором решается совокупностьвзаимосвязанных задач, обеспечивающая решение одной – двух более сложных задач, которые предлагаются в совокупности последними.
Методы бучения – проблемное обучение (на основе активизации и интенсификации деятельности учащихся)
Формы обучения – индивидуальный, фронтальный опрос, групповые способы обучения (на основе эффективности организации учебного процесса)
Средства обучения – компьютер; презентация, подготовленная учителем, в PowerPointили, при наличии, для интерактивной доски.
Цели урока:
дидактическая цель – систематизировать знания по разделу «Нахождение площадей фигур с помощью определенного интеграла», формировать умения устанавливать взаимосвязи между задачами;
развивающая цель – развивать мыслительные операции (анализ, синтез, обобщение и т.д.);
воспитательная цель – формировать потребности у обучающихся в дальнейшем изучении предмета.
Диагностируемые цели (ожидаемые результаты):
по окончании урока обучающиеся:
- знаютсхему нахождения площади фигуры с помощью определенного интеграла;
- умеют решать дидактические задачи (находить площади фигур, ограниченных следующими линиями: графиком функции, осью ОХ, прямыми х = а, х = в; графиком функции и осью ОХ; графиками двух функций и осью ОХ; графиками двух функций и прямыми х = а, х = в; графиками двух функций).
- умеют переформулировать условия задачи, устанавливать связи между задачами, т.е. осуществлять аналитико-синтетическую деятельность.
1 урок – обобщение, закрепление, применение знаний в стандартных ситуациях (мотивационно-ориентировочная часть,тренировка);
2 урок – применение знаний в задачах повышенной трудности (содержательная часть,
совершенствование полученных знаний и навыков).
Ход урока
Мотивационно-ориентировочнаячасть
Умение решать задачи - практическое искусство,
подобное плаванию или катанию на лыжах,
или игре на фортепиано: научиться этому можно
лишь подражая избранным образцам
и постоянно тренируясь...
Дьёрдь Пойа(слайд 2)
1 этап
На этом этапе идет одновременная работа по следующим направлениям:
— 1ый ученик должен из предложенных слов, словосочетаний (при необходимости изменяя окончания слов) продолжить утверждение: «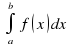 равен …» (слайд 3);
равен …» (слайд 3);
— 2ой ученик на доске готовит основные виды задач на нахождение площадей фигур с помощью определенного интеграла (чертеж, описание чертежа, формула)(на доске);
— остальные учащиеся в это время работают на месте с ЛПО, для каждого случая дать описание чертежа, записать формулу для нахождения площади фигуры;
— 3ий ученик получает индивидуальное задание за компьютерным столом(приложение 1).
2 этап
На этом этапе идет проверка выполнения выданных заданий в том порядке, в котором были выданы.
— 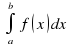 равен разности значений первообразной для функции y = f(x)наотрезке [a;b] или приращению первообразной для функции y = f(x)наотрезке [a;b];
равен разности значений первообразной для функции y = f(x)наотрезке [a;b] или приращению первообразной для функции y = f(x)наотрезке [a;b];
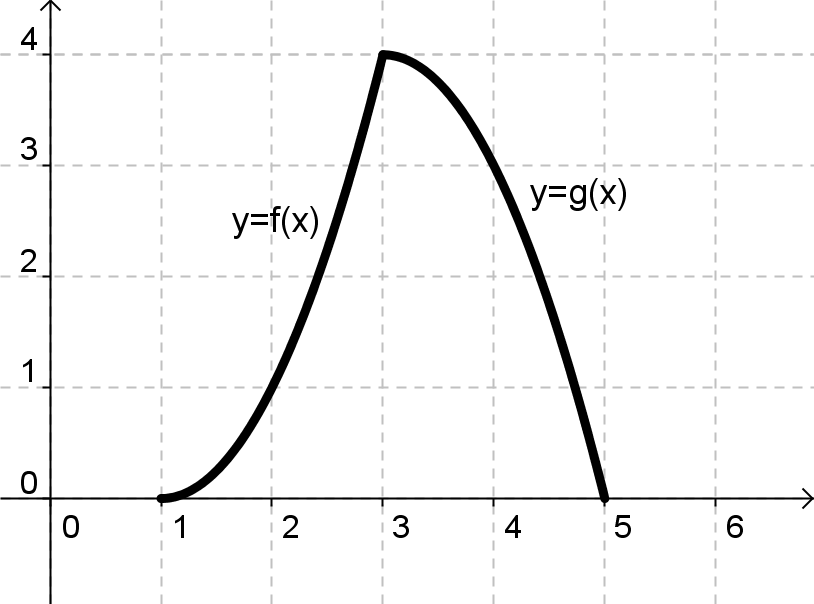
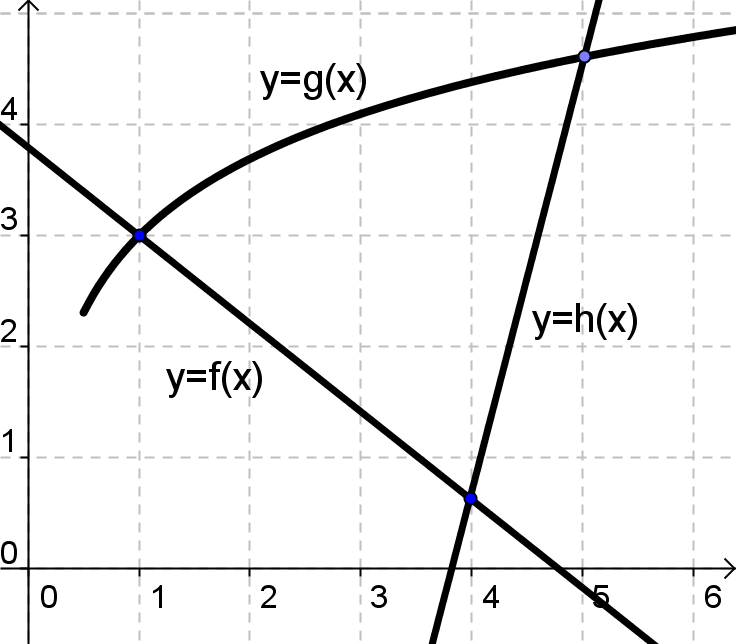
— учащийся должен предоставить для ответа следующие фигуры:
ограниченнаяграфиком функции y = f(x), осью ОХ, прямыми х = а, х = в, где f(x)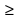 0 на [a;b];
0 на [a;b];
ограниченнаяграфиком функции y = f(x), осью ОХ, прямыми х = а, х = в, где f(x)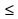 0 на [a;b];
0 на [a;b];
ограниченная графиком функций y = f(x), y = g(x), осью ОХ, прямыми х = а, х = в, где f(x)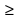 g(x) на [a;b].
g(x) на [a;b].
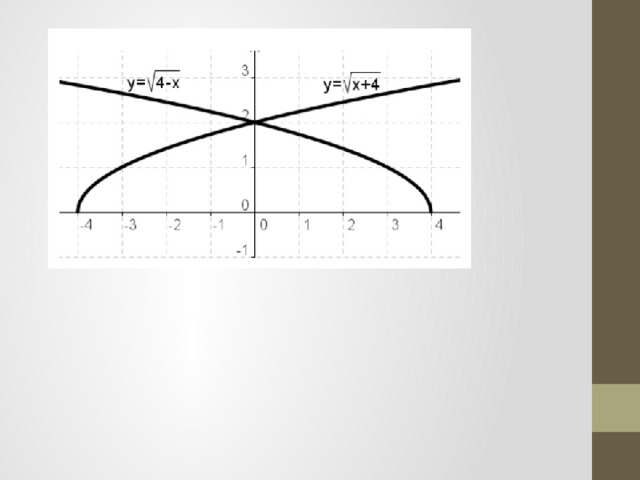
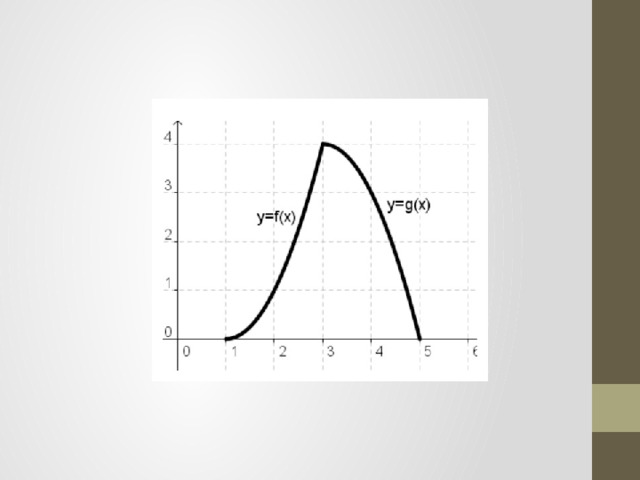
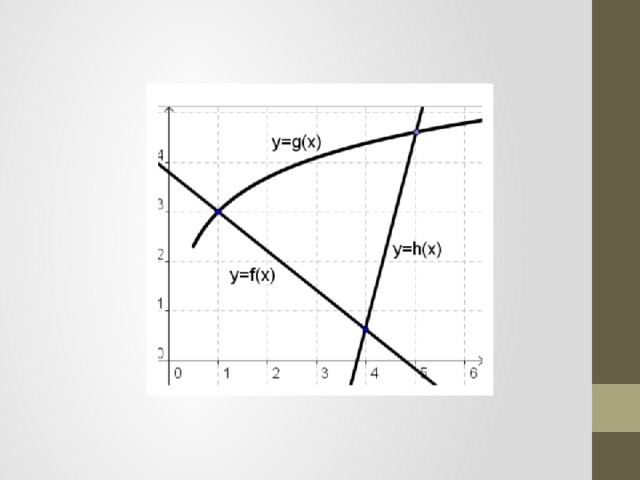
— работа с чертежами ЛПО (слайды 4 – 6)
— ответ ученика, получившего индивидуальное задание (чертеж проецируется на интерактивную доску или выполняется на обычной доске для дальнейшей работы)
3 этап
Работа с чертежом:
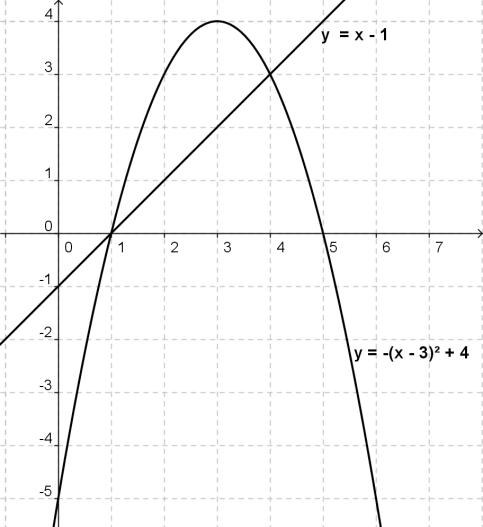
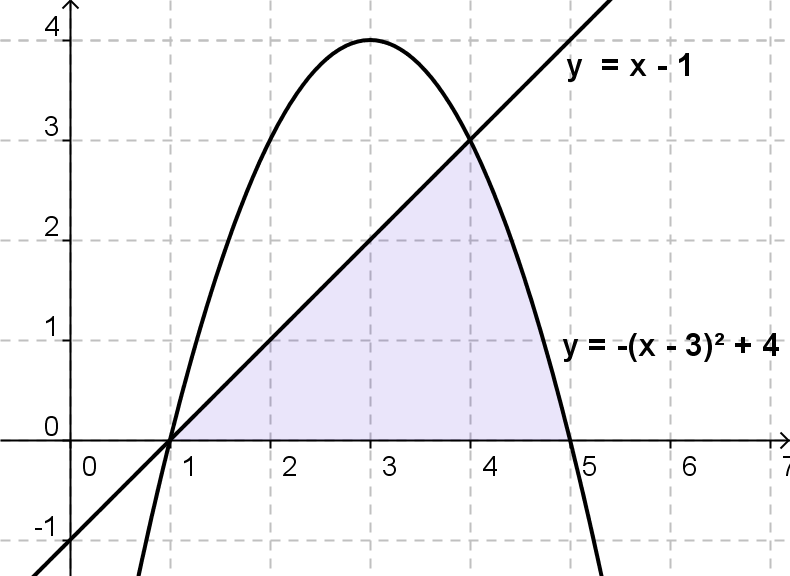
— найдите фигуры, которые ограничены в том числе и построенными графиками
| 1 вариант | 2 вариант | 3 вариант |
| 
| 
| 
|
— найдите площади указанных фигур (работа выполняется на местах по вариантам и по 1 ученику с каждого варианта на доске с последующей проверкой)
Подведение итогов первой части:
умеем выделять фигуры, ограниченные заданными линиями;
умеем находить площади фигур, используя определенный интеграл, следуя «избранным образцам».
Содержательная часть
Решение задач повышенного уровня сложности
Процесс решения задачи представляет собой
поиск выхода из затруднения или пути обхода препятствия,
- это процесс достижения цели,
которая первоначально не кажется доступной…
Дьёрдь Пойа(слайд 7)
Задача №1: Вычислить 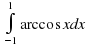
Вопросы к задаче:
— Дайте определение определенного интеграла с точки зрения геометрической модели.
(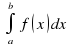 равен площади криволинейной трапеции, ограниченнойграфиком функции y = f(x), осью ОХ, прямыми х = а, х = в, где f(x)
равен площади криволинейной трапеции, ограниченнойграфиком функции y = f(x), осью ОХ, прямыми х = а, х = в, где f(x)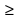 0 на [a;b])
0 на [a;b])
— Каков план решения задачи?
(Построить фигуру, ограниченную графиком функции y = arcccosx,х =1, х = –1, у = 0;
найти ее площадь используя геометрические формулы)
— (слайд 8) Выбрать на каком чертеже находится график функции y = arcccosx, каковы особенности этого графика (симметрия относительно точки 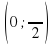 ).
).
— Какова идея решения задачи? (Данный интеграл равен площади фигуры,ограниченной графиком функции y = arcccosx,х =1, х = –1, у = 0, площадь которой равна половине площади прямоугольника со сторонами 1 и  единиц)
единиц)
— Вычислите значение интеграла.
Задача №2 выполняется при наличии времени или ее можно включить в домашнее задание вместе с задачей на дополнительную оценку.
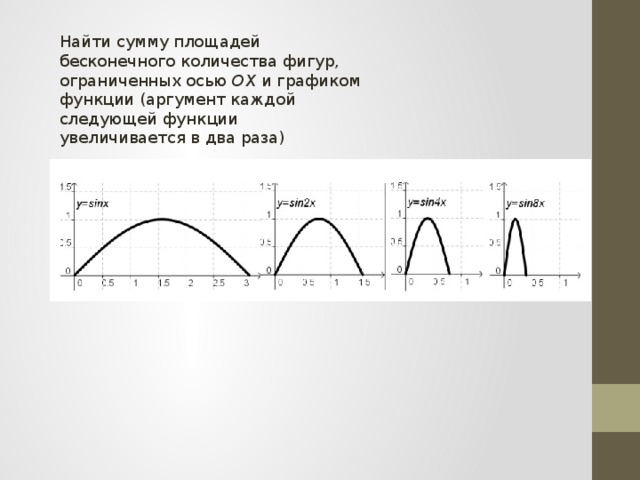
Задача №2:Найти сумму площадей бесконечного количества фигур, ограниченных осью ОХ и графиком функции (аргумент каждой следующей функции увеличивается в два раза)
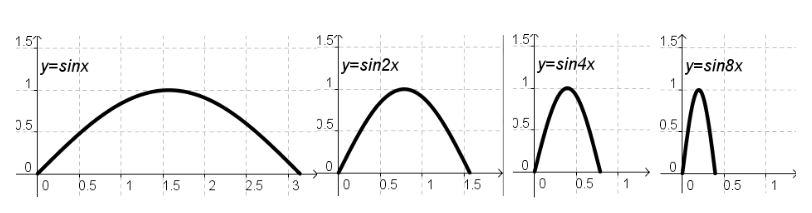
Рефлексивно-оценочная часть
Подведение итогов второй части:
Умеем применять на практике не только алгебраическую (аналитическую) модель определенного интеграла, но и его геометрическую модель.
Понимаем, что площади фигур считаются не ради изучения интеграла, а интеграл изучается ради вычисления площадей
Рефлексия.
Оцените свою работу на урок
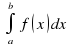 равен …» (слайд 3);
равен …» (слайд 3);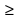 0 на [
0 на [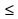 0 на [
0 на [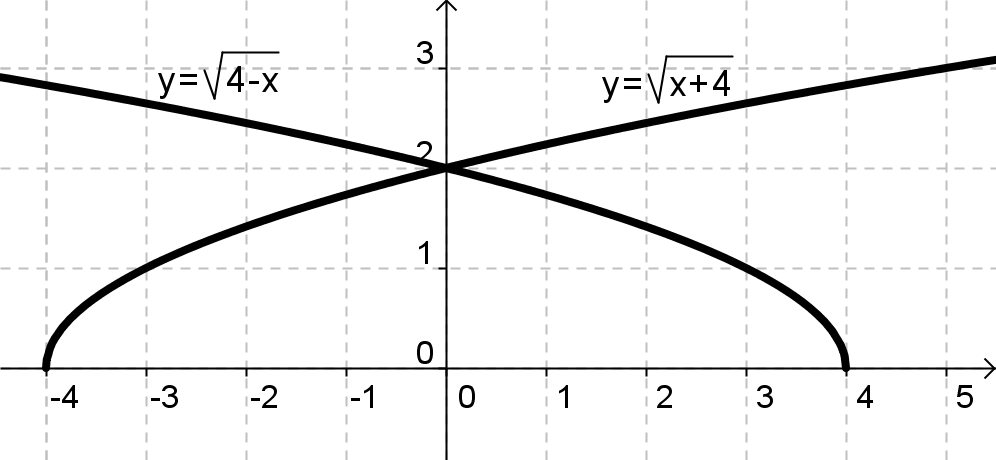




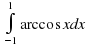
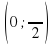 ).
). единиц)
единиц)