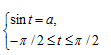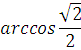Сабақтың тақырыбы: Қарапайым тригонометриялық теңдеулер және
оларды шешу (cost = a, sint = a)
Сабақтың мақсаты:
Білімділік: қарапайым тригонометриялық теңдеулерді шешуде формуланы дұрыс пайдалану,білім-білік дағдыларын қалыптастыру.
Дамытушылық: ой-өрісін дамыту , есте сақтау қабілетін арттыру,теориялық білімін практикада қолдана білу дағдысын қалыптастыру.
Тәрбиелілік: шапшаңдыққа, ізденімпаздыққа, тиянақтылыққа, ұжымдық ауызбіршілікке тәрбиелеу
Сабақтың көрнекілігі: деңгейлік тапсырмалар, компьютер, ақпараттық құралдар.
Сабақтың түрі: топтық жұмыс
Сабақтың өту әдісі: аралас , іздену, өзін-өзі тексеру, талдау.
Сабақтың барысы:І. Ұйымдастыру кезеңі.
а) оқушыларды түгелдеу
ә) сабақ мақсатымен таныстыру
ІІ. Үй жұмысын тексеру.
а) екі оқушы тақтаға үйге берілген есепті орындайды
ә) Тигонометрия туралы тарихи мәлімет.
б) қалған оқушылар ауызша сұрақтарға жауап береді
1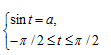

 . асанының арксинусы деп синусы асанына тең �
. асанының арксинусы деп синусы асанына тең �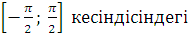 �α бұрышын айтады.Егер �
�α бұрышын айтады.Егер � �1болса онда arcsin a = t
�1болса онда arcsin a = t
2 . а санының арккосинусы деп косинусы а санына тең �
. а санының арккосинусы деп косинусы а санына тең � �кесіндісіндегі α бұрышын айтады
�кесіндісіндегі α бұрышын айтады
Егер � �1болса онда arccos a = t
�1болса онда arccos a = t
ІІІ.Ауызша тапсырмалар
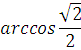
arcsin (-1)=
arcсos о =
�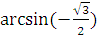 �
�
� �
�
arcсos 1=
�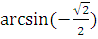 �
�
� �
�
arcsin � �
�
arcsin(- � �)
�)
arcsin 1
arcсos� �
�
arcsin 0
Дұрыс жауаптар:
| � � � | 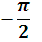
| 
| 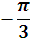
| 0 | 
| 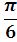
| -�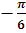 � � | 
| 
| 0 |
| Т | Ә | У | Е | Л | С | І | З | Д | І | К |
Мәндерін дұрыс тапқанда , «ТӘУЕЛСІЗДІК» сөзі шығады . Оқушыларға теуелсіз елдің ұрпақтары білімді, сауатты болу керектігін ұғындыру.
ІУ.Қарапайым тригонометриялық теңдеулерді шешудің дербес жағдайлары /дұрыс жазуды сәйкестендір
| sin x = 0 | 
|
| cos x = -1 | 
|
| sin x = 1 | 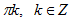
|
| cos x = 1
| 
|
| cos x = 0 | 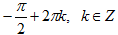
|
| sin x = - 1
| 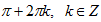
|
Теңдеулерді шешуді қарастырайық.
cost=а t=± arccosa + 2πк, к €Z sint=a t=(-1)n arcsina +πn, n€Z
Теңдеуді шешіңдер ( ауызша)
sin х= 
c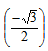 osх =
osх =
-2sin х= 1
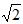 cosх = 1
cosх = 1
У. « Қарапайым тригонометриялық теңдеулерді шешу» тақырыбы бойынша білімдерін тексеру. / Екі нұсқада тапсырма беру/
| 1-нұсқа
| 2-нұсқа |
| cos x =a теңдеуінің �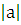 �1болғандағы шешімі қандай? �1болғандағы шешімі қандай? | sin x = a теңдеуінің �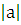 � 1болғандағы шешімі қандай? � 1болғандағы шешімі қандай?
|
| а-ның қандай мәнінде cos x = a теңдеуінің шешімі болады? | а-ның қандай мәнінде sin x = a теңдеуінің шешімі болады? |
| Бұл шешім қандай формуламен өрнектеледі? | Бұл шешім қандай формуламен өрнектеледі? |
| cos x = a теңдеуді шешу барысында а –ның мәні қай оське ығысады?
| sin x = a теңдеуді шешу барысында а –ның мәні қай оське ығысады?
|
| arccos a қандай аралыққа тиісті?
| arcsin a қандай аралыққа тиісті?
|
| arccos(- a) неге тең ?
| arcsin (- a) неге тең ?
|
Өзара тексеріп, бағалайды.
Дұрыс жауаптар
| 1-нұсқа | 2-нұсқа.
|
| Шешімі жоқ | Шешімі жоқ |
| |a| | |a|
|
| 
|
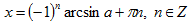
|
| Ох осіне |
Оу осіне |
| [0;π] |
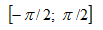
|
| π - arccos a |
-arcsin a |
УІ. а) Оқулық бойынша есептер шығару .
№105. а)�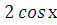 �=�
�=�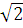 � , �
� , �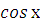 �=�
�=�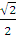 � , х=±�
� , х=±�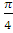 �+2πn , n€£
�+2πn , n€£
ә) �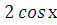 �=-1, �
�=-1, �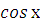 �=-�
�=-� � , х=±�
� , х=±� �+2πn , n€£
�+2πn , n€£
б) 2�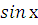 �=1, �
�=1, �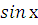 �=�
�=� �, х=�
�, х=� � +πn , n€£
� +πn , n€£
№106(а, ә ) №107(а, ә) есептерді шығарту
ә) /Деңгейлік тапсырмалар шығарту ,өз бетінше орындау)
|
| Деңгейлік тапсырмалар | 1 | 2 | 3 |
| 1 | /І-деңгей/ -2sin х= 1
| х=� � +πn , n€£ � +πn , n€£
| х=� � +πn , n€£ � +πn , n€£
| х=�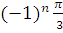 � +πn , n€£ � +πn , n€£
|
| 2 | /І-деңгей/ -� �=1 �=1 | х=±� �+πn , n€£ �+πn , n€£
| х=±�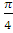 �+2πn , n€£ �+2πn , n€£ | х=±� �+2πn , n€£ �+2πn , n€£ |
| 3 | /ІІ-деңгей/ � �=� �=�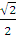 � � | х=� � +πn , n€£ � +πn , n€£
| х=�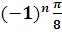 � +� � +� �n , n€£ �n , n€£
| х=�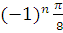 � +πn , n€£ � +πn , n€£
|
| 4 | /ІІ- деңгей/ �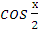 �=0 �=0 | х=�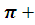 �2πn , n€£ �2πn , n€£
| х=�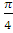 �+2πn , n€£ �+2πn , n€£ | х=� �+πn , n€£ �+πn , n€£ |
| 5 | /ІІІ- деңгей/ �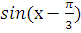 �=-1 �=-1 | х=� � +πn , n€£ � +πn , n€£
| х=�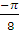 � +πn , n€£ � +πn , n€£
| х=� � +2πn , n€£ � +2πn , n€£
|
| 6 | /ІІІ- деңгей/ �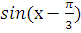 �=1 �=1 | х=�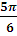 � +2πn , n€£ � +2πn , n€£
| х=�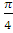 �+2πn , n€£ �+2πn , n€£ | х=�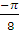 � +πn , n€£ � +πn , n€£
|
Дұрыс жауаптар:1)2, 2)3, 3)2, 4)1, 5)3, 6)1.
УІІ.Сабақты қорытындылау:
Ауызша жұмыстарды бағалау
Кері тригонометриялық функциялар
Тригонометриялық теңдеулерді шешудің дербес жағдайлары
Қарапайым тригонометриялық теңдеулерді шешу
Сыныптағы орындалған тапсырмаларды тексеру
УІІІ.Үйге тапсырма беру: №101 ,№ 109, №110