"Изготовление витража" интегрированный урок

Открытый интегрированный урок в 7-м классе (геометрия + черчение)

«Изготовление витража»

ГБОУ ШКОЛА №1106

учитель математики: Егорова О.Б.,

учитель черчения: Мясникова И.В.

москва 2014

Открытый интегрированный урок в 7-м классе (геометрия + черчение)

«Изготовление витража»

учитель математики: Егорова О.Б., учитель черчения: Мясникова И.В.

Цель: показать неразрывность связей между предметами эстетического и естественно-математического блоков

Задачи:

1. Систематизировать и обобщить знания учащихся

2. Развить логическое мышление и внимательность

3. Воспитывать внимательность и аккуратность в выполнении чертежей

4. Воспитывать любовь и уважение к красоте духовного мира и накопленному на протяжении тысячелетий наследию народов

Тип урока: урок закрепление

Оборудование: интерактивная доска, чертежные принадлежности, карточки для изготовления чертежа витража, бумага формата А4

План урока:

1. Организационная часть

2. Историческая справка о происхождении витражей

3. Повторение и закрепление материала

4. Окружность в декоративном – прикладном искусстве

5. Практическая работа

6. Подведение итогов

7. Творческое домашнее задание

Ход урока

1. Организационная часть

Здравствуйте ребята! Сегодня у нас не совсем обычный урок. Вести его будут два учителя: геометрии и черчения. Как вы думаете, почему? .....

Действительно, мы сегодня в очередной раз убедимся, что знания, полученные на одном уроке, обязательно пригодятся на других. В конце урока вы сами докажите это.

1. Историческая справка

Ребята, сегодня мы хотели бы поговорить о витражах. А как и когда они появились нам расскажет Анастасия.

Презентация1

1. Повторение и закрепление материала

Учитель геометрии: ребята, какие геометрические фигуры и тела мы можем видеть на витражах? (круг, квадрат, треугольник, конус, цилиндр, призма, пирамида)

Учитель геометрии: все эти геометрические фигуры и тела мы можем построить используя принцип деления окружности на равные части. Давайте вспомним определение окружности и ее элементов.

-Окружность – это множество точек плоскости, равноудаленных от заданной точки, которая называется центром окружности.

- Расстояние от центра окружности до любой ее точки называется радиусом.

- Отрезок, соединяющий любые две точки окружности, называется радиусом.

- Хорда, проходящая через центр окружности, называется диаметром.

- формула, связывающая радиус и диаметр.

d=2r, r=0,5d

Учитель черчения: для того чтобы наши витражи получились красивыми, давайте повторим деление окружности на 4 и 8, 3, 6 и 12 частей.

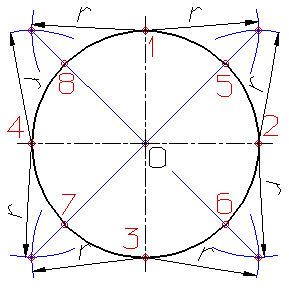
1: Деление окружности на восемь равных частей производится в следующей последовательности:

Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;

Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы  прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.

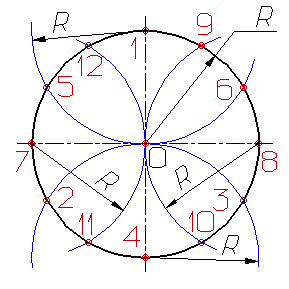
2: Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности:

Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью

Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;

Точки 1, 2 и 3 делят окружность на три равные части;

Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;

Точки 1 - 6 делят окружность на шесть равных частей;

Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;

Точки 1 - 12 делят окружность на двенадцать равных частей.

1. Окружность в декоративном – прикладном искусстве

А сейчас давайте посмотрим как использовалась окружность в декоративном – прикладном искусстве.

Презентация2

1. Практическая работа

Выполнение чертежей.

Учитель черчения: А теперь мы с вами построим по карточкам возможные витражи, применяя основные правила построения. (по ходу работы помогаем ученикам в построении).

1. Подведение итогов

Итак, ребята, сегодня мы убедились, что знания полученные на одних уроках, помогают на других. Отметить лучших учащихся.

1. Домашнее задание

А дома, ребята, вы раскрасите свои витражи, и мы устроим выставку ваших работ!

Спасибо за урок! До свидания.

Список литературы:

Геометрия 7-9 класс" Атанасян Л.С.

Черчение, 7-8 класс, Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С

Витраж

Что такое витраж?

Витражами называются прозрачные картины, рисунки, узоры, выполняемые из стекла или на стекле

История возникновения

• Витражи, представлявшие ранее набор цветных стекол, нередко служили случайным украшением помещения;
• с течением времени совершенствовалась их композиция, рисунок, художественная обработка стекла и техника исполнения.

Назначение витражей

• они являются богатым декоративным украшением зданий и отдельных помещений,
• заменяют оконные стекла и дверные филенки.
• пропускают свет и дают возможность изолировать помещения первых этажей от посторонних взглядов.

Собор Парижской Богоматери

(Нотр – Дам – де –Пари)

Строился с 1163 по 1345 г.г.

В России витражи существовали еще в XII веке, однако они не были характерным элементом убранства интерьеров русских домов .