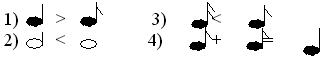Интегрированный урок по математике и музыке в 5-м классе по теме "Дроби и ноты"

Интегрированный урок по математике и музыке в 5-м классе

 по теме "Дроби и ноты"

Цель урока: Закрепление знаний учащихся об обыкновенных дробях (сложение дробей с одинаковыми и разными знаменателями, сравнение дробей).

Задачи урока:

1. Обобщение понятий о дробях на основе их распространения на ситуации с нотами.
2. Закрепление видения нот, как своеобразной (без цифровой) знаковой формы дробей.
3. Расширение кругозора учащихся. Воспитание интереса и увлечения к изучаемому предмету.

Оборудование.

• Опорная схема “Дроби и ноты”.
• Раздаточные карточки.
• Задания для учащихся, оформление в виде плакатов.
• Пианино.

Ход урока

1. Организационный момент.

– Здравствуйте, ребята!

– Сегодня у нас урок-закрепление по теме: “Дроби и ноты”.

– Он у нас необычный. Мы будем заниматься математикой и музыкой.

– На этом уроке мы должны закрепить знания об обыкновенных дробях: сложение дробей с одинаковыми и разными знаменателями, сравнение дробей; закрепить видение нот как своеобразной знаковой формы дробей.

Класс разделён на две группы, которые будут соревноваться.

2. Повторение.

Мы живем в мире звуков. Люди давно научились записывать различные звуки с помощью специальных знаков. Звуки человеческой речи, например, записываются с помощью букв, а музыкальные звуки записываются с помощью нот.

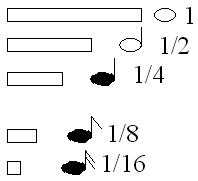
– На уроках музыки вы изучали ноты,  длительность звучания. Так вот, ноты отличаются по длительности их звучания. Самая “длинная” нота – целая. Ее обозначают знаком. С точки зрения математики целую ноту можно принять за единицу (1). Давайте послушаем, как долго звучит эта нота (звучит цельная нота).

– Запишем – целая 1. Какой счет ведется при целой ноте? (1 и 2 и 3 и 4 и)

– Нота вдвое короче называется половинной и обозначается.

 Послушаем длительность звучания половинной ноты (звучит половинная нота). Какая же дробь соответствует половинной ноте? Половинной ноте соответствует дробь 1/2. Какой счет при половинной ноте? (1 и 2 и)

– Запишем – половинная 1/2.

– Послушаем ноту, которая еще в два раза короче (звучит нота). Это четвертная.

– Запишем – четвертная 1/4. А как считается она? (1 и )

– Восьмая нота имеет еще меньшую длительность. Слушаем (звучит нота).

– Запишем – восьмая 1/8. Какой счет ведется при этой ноте? (1 или и)

– И, наконец, самая короткая нота шестнадцатая (звучит нота). На две ноты приходится счет 1 или и.

– Запишем – шестнадцатая 1/16.

3. Закрепление.

– Ребята, обратимся к опорной схеме “Дроби и ноты”.

– Какая же нота имеет наименьшую длительность?

– А какая наибольшую  длительность?

– Хорошо, молодцы!

– Ребята! Сравним длительности звучания таких нот.

 Выдаются карточки № 1

Для того чтобы выполнить это задание запишем ноты через дроби. Итак, сравним. У доски работают по одному из каждой группы, четные одна группа, нечетные – другая.

На карточке №1 вы видите эти дроби, вам необходимо поставить знаки <, > или =, соответственно сравнить длительность звучания данных нот.

Сформулируйте правило, которое использовали при сравнении этих дробей (из двух дробей с равным числителем больше  та, у которой знаменатель меньше).  Проверьте друг друга и поставьте оценки.

Но в музыке не используется знак “+”, поэтому равенства длительностей нот лучше записывать так: выдаются карточки № 2. По одному ученику с каждой группы выходят и проверяют равенства. Первая группа – а, вторая – б.

Проверим эти равенства на доске.

а) 1/2 + 1/4 + 1/4 = 2/4 + 2/4 = 4/4 = 1;

б) 1/8 + 1/16 + 1/16 = 1/8 + 2/16 = 1/8 + 1/8 = 2/8 = 1/4.

В приведенных равенствах одной ноты не хватает: выдаются карточки № 3

Найдите недостающую ноту (самостоятельно). Обменяйтесь ответами и поставьте оценку.

Посмотрим теперь на нотный стан, изображенный на плакате и на раздаточных карточках № 4.

Из рисунка мы видим, что нотная запись разбита вертикальными линиями на отдельные части: каждая такая часть называется тактом.

Посчитаем общую длительность всех нот, входящих в каждый такт (все ответы запишем в виде дроби со знаменателем 4): Обменяйтесь ответами и поставьте оценку.

1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4;

1/4 + 1/8 + 1/8 = 1/4 + 2/8 =1/4 + 1/4 = 2/4;

1/4 + 1/4 = 2/4;

1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4;

1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4.

Как видим, в каждом случае мы получили одно и то же число 2/4. Это число называется размером музыкального произведения и записывается в начале нотного стана.

Теперь послушаем это произведение, с нотной записью которого мы работали. Угадайте название этой песни. Ученик играет на пианино.

(Русская народная песня “Во поле береза стояла”).

На карточке № 5 записана мелодия без разбиения на такты. Сделайте самостоятельно, зная размер произведения – 2/4.

1. 1/8 + 1/8 = 2/8 = 1/4 + 1/8 = 2/8 + 1/8 = 3/8 + 1/8 = 4/8 = 2/4;
2. 1/4 + 1/4 = 2/4;
3. 1/8 + 1/8 + 1/8 + 1/8 = 2/4;
4. 1/4 + 1/4 = 2/4;
5. 1/4 + 1/8 + 1/8 = 1/4 + 2/8 = 1/4 + 1/4 = 2/4;
6. 1/4 + 1/8 + 1/8 = 2/4;
7. 1/8 + 1/8 + 1/4 = 2/4;
8. 1/4 + 1/4 = 2/4.

Послушаем эту мелодию и угадаем название песни.

(Белорусская народная песня “Перепелочка”).

И последнее задание тест-обобщение “Дроби”.

1. Какие из высказываний относительно дробей   ,     ,    ,      неверны?

а) Числители всех дробей равны 1.
б) Знаменатели являются четными числами.
в) Дроби соответствуют длительности звучания разных нот.
г) Эти дроби нельзя сравнить.

2. Какая из этих дробей является наибольшей?

а)   , б)    , в)   , г)                                       

3. Какая из этих дробей является наименьшей?

а)   , б)    , в)     , г)                                     

4. В каком порядке расположены дроби   ,  ,   ,     ?

А) Возрастания.
б) Убывания.

4. Подведение итогов урока.

• Ну что, ребята, наш урок  подошел к концу.
• Оценки за устные  ответы и работу в команде.
• Домашнее задание № 927, 928.
• Ребята, что же мы узнали на уроке?
• Вообще, нужны ли нам дроби?
• Исполним песню “О дробях”.

О дробях. (На мотив песни “Чему учат в школе”).

Дроби всякие нужны,
Дроби разные важны.
Дробь учи, тогда сверкнет тебе удача.
Если будешь дроби знать,
Точно смысл понимать,
Станет легкой даже трудная задача.
Дробь свою “переверни”, (это слово обсуждаем)
Повнимательней взгляни.
Вдруг из правильной неправильную видишь.
Эти дроби перемножь,
Единицу ты найдешь,
Их обратными зови и не обидишь.
Дробь на дробь чтоб разделить,
Долго нечего мудрить.
Дробь обратную делителю берете.
И на эту дробь теперь
Умножайте поскорей,
Так искомое вы частное найдете.

Спасибо, ребята, за работу на уроке. Спасибо гостям!