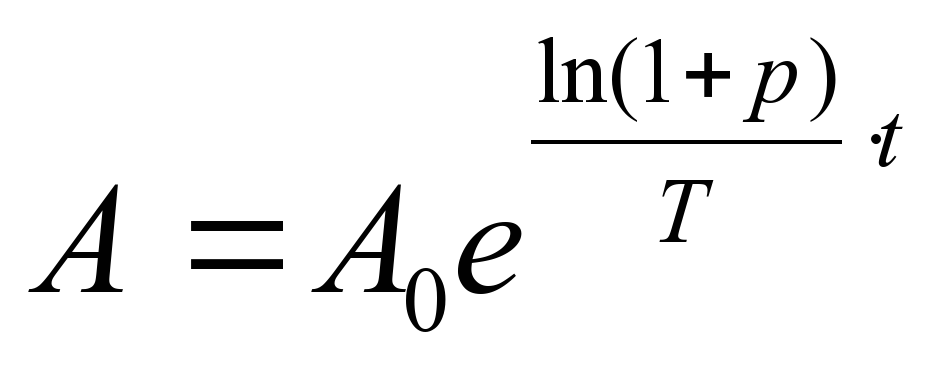Интегрированный урок (математика, литература) 11 класс. Решение трансцендентных уравнений.

Предмет:    Алгебра и начала анализа.

 

Класс:           11

 

 

Тема:  Решение трансцендентных уравнений.

 

 

Цель урока: повторить и обобщить  знания в решении трансцендентных уравнений.

 

 

 

Задачи урока:

 

Образовательные

-повторить решения трансцендентных уравнений основными способами;

-показать применения трансцендентных уравнений в различных областях науки;

-использовать дифференцированный подход в решении задач различного уровня сложности.

 

Развивающие

-развитие познавательного интереса учащихся;

-развитие навыков самоконтроля;

-развитие умений обобщать и конкретизировать формулы при решении задач.

 

Воспитательные

-воспитание уважительного отношения друг к другу;

-воспитание настойчивости для достижения конечного результата при решении трансцендентных уравнений;

-развитие мышления, речи, творческой активности.

 

 

 

 

Оборудование:

 

1. Плакат

 «Некоторые виды трансцендентных функций открывают доступ ко многим исследованиям»

             Л.Эйлер

 

1. Плакат « Математический лабиринт».
2. Карточки с заданиями по вариантам.
3. Плакат в виде книги с надписью:

М.Е.Салтыков – Щедрин «Господа Головлевы».

1. Дифференцированные карточки для игры «Поле чудес».
2. Табло для игры «Поле чудес».
3. Переносные доски, маркеры, мел.
4. Плакат с критерием оценки.

 

 

Структура урока

1. Организационный момент
2. Постановка цели урока.
3. Проверка домашнего задания.
4. Решение трансцендентных  уравнений по вариантам.
5. Решение прикладных задач.
6. Игра «Поле чудес».
7. Рефлексия.
8. Подведение итогов урока.
9. Постановка домашнего задания.

 

 

 

 

 

 

Ход урока.

 

 

1. Организационный момент.

 

Приветствие учащихся. Проверка готовности класса к уроку.

 

1. Постановка цели урока.

 

     Ребята, сегодня на уроке мы с вами осуществим погружение в мир уравнений. Сегодня на уроке нас будут интересовать только те уравнения, которые мы изучили в 10-11 классах  в курсе алгебры и начал анализа, а именно, трансцендентные.

      Трансцендентный – означает «превосходящий», подразумевается по Эйлеру, превосходящий силу алгебраических методов.

     Итак, какие же уравнения называются трансцендентными?

 Ответ учащихся: трансцендентные уравнения – это уравнения, содержащие трансцендентные функции, а именно, логарифмические, показательные, тригонометрические и обратные тригонометрическим.

     Сегодня на уроке нам нужно показать знание методов решения показательных и логарифмических уравнений и показать применение теоретического материала при  решении прикладных задач.

 

1. Проверка домашнего задания.

 

Домашнее задание предлагалось в виде «Математического лабиринта»  (см. Приложение к уроку «Математический лабиринт»). Аналогичная карта оформлена на доске ( на плакате).

     Итак, ребята откройте тетради, давайте проверим правильность выполнения домашнего задания и заполним «Математический лабиринт», оформленный на плакате.

     Ребята называют полученный результат каждого уравнения и кратко говорят о методе решения уравнения. Учитель заполняет лабиринт на доске.

 

После проверки домашнего задания обратить внимание ребят на рабочие листы, которые есть у каждого на парте ( см. Приложение к уроку «Рабочая карта»). На этом листе три колонки:

-этапы урока

-количество баллов

-без названия 

 

Ребята, каждый этап урока вы должны будете оценить себя  по десятибалльной системе.

Итак, первый этап «Математического лабиринта». Оцените себя.

 

 

1. Решение трансцендентных уравнений.

 

    Откройте тетради и запишите число и тему урока. Следующий этап мы будем работать по двум вариантам. Запишите в  тетради номер варианта.

     На партах лежат карточки с заданиями для каждого варианта. Решаем задание №1( см. Приложение к уроку «Задания для самостоятельной работы»).

Двое учащихся разных вариантов вызываются к доске и оформляют задание на доске. Решения проверяются всем классом, исправляются ошибки.

     После проверки ребята оценивают себя по десятибалльной системе и заполняют соответствующую графу в рабочих листах.

 

 

1. Решение прикладных задач.

 

     Очень часто при решении различных задач используются трансцендентные функции. Назовите, при решении каких задач используются решения трансцендентных уравнений?

Ответ учащихся:

-радиоактивный распад;

-зависимость давления от высоты;

-зависимость скорости  ракеты от массы;

-определение степени поглощения и т.д.

  

     А сейчас уделим минутку литературе. Вы знакомы с произведением М.Е.Салтыкова-Щедрина «Господа Головлевы». Читая это произведение, трудно представить, что здесь используется решение трансцендентных уравнений.

Итак, послушайте:

«Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными накладками листы бумаги. На этот раз его занимает вопрос: сколько бы у него было денег, если бы маменька, подаренные ему при рождении дедушкой 100 рублей, не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного всего 800 рублей».

 

     Учитель открывает на доске плакат в виде книги, под которым записана краткая запись этой задачи и просит ребят рассказать, какие величины даны в условии текста, пользуясь экономическим  терминами.

 

 

 

 

 

А=100 рублей

В=800 рублей

Р=?

Т=1 год

t = ?

 

 

Вопросы к задаче:

-Почему возросла сумма?

-Отчего зависит конечная сумма?

-Установите связь между величинами

 

 

Итак, что можно определить по этой формуле?

- процент ломбарда

-возраст Порфирия Владимировича.

 

Работаем по вариантам.

 

Таблица оформлена на переносной доске.

 

 

1

2

А

100

100

А

800

800

Р

4%

?

t

?

50

 

 

Задание 1 варианта :

Определить возраст Порфирия Владимировича, если известна процентная ставка ломбарда.

 

Задание  2 варианта:

Определить процентную ставку ломбарда, если известен возраст Порфирия Владимировича.

 

После решения этой задачи результат записывается в таблицу.

Приступаем к выполнению задания 2 на карточках( см. приложение к уроку «Задание для самостоятельной работы»).

Двое учащихся разных вариантов записывают решение задач на доске, затем класс проверяет и исправляет ошибки. После проверки ребята оценивают себя и ставят балл в рабочий лист.

 

Ребята, подтверждением последних уроков алгебры являются слова великого математика Л.Эйлера: «Некоторые виды трансцендентных функций открывают доступ ко многим исследованиям».

Изучая трансцендентные функции, решая трансцендентные уравнения, мы для себя сделали небольшие открытия.

 

1. Игра «Поле чудес»

 

      Сейчас поиграем в игру «Поле чудес». У каждого на парте лежат карточки трех цветов: красные, зеленые, синие. На каждой карточке написано, какое максимальное количество баллов вы сможете заработать, решив правильно предложенные уравнения. Задания даны по уровню сложности. Вы набираете карточку, решаете уравнение, по ответу этого решения выбираете букву, а номер карточки указывает на позицию этой буквы во фразе.

 

1

2

 

3

4

5

6

 

7

8

 

9

10

11

12

н

и

п

у

х

а

н

и

п

е

р

а

 

13

14

 

15

16

17

18

19

20

21

22

 

23

н

а

э

к

з

а

м

е

н

е

!

 

 

После решения задания и расшифровывания фразы ребята оценивают себя.

 

1. Рефлексивно – диагностический этап.

 

В рабочих листах осталась незаполненной одна колонка. Ребята, закрасьте поле каждого этапа тем цветом, который отражает ваше настроение на каждом этапе урока.

 

 

1. Подведение итогов.

 

Посчитайте количество баллов и выставите себе оценку согласно критерию.

Критерий оценки:  34-40 баллов –«5»

                                 22-33 баллов –«4»

                                 20-27 баллов –«3»

 

Учитель просит поднять руки ребят, кто заработал оценку «4» и «5»

Тетради и рабочие листы сдаются учителю.

Учитель благодарит ребят за хорошую работу на уроке.

 

1. Постановка домашнего задания.

 

Каждому ученику предложено домашнее задание на карточке ( см. приложение к уроку «Домашнее задание»).