Алгебра, 9 класс 7.10.2015
Урок № 16
Тема. Графики функций 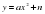 и
и 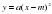 .
.
Цель: Способствовать:
а) формированию знаний основных понятий, входящих в тему;
б) выработке умений работать самостоятельно с теоретическим материалом на уровне анализа и вычленения главного;
в) умению строить графики функций вида y=ax2 + n и y=a(x-m) 2.
Задачи урока:
Образовательные:
- формировать навыки построения графиков функций в ходе урока и самостоятельной работе;
- развивать умение и навыки учащихся работать самостоятельно с теоретическим и практическим материалом на уровне анализа вычленения главного.
Развивающие:
- развивать критическое мышление;
- развивать познавательную активность.
Воспитательные:
- содействовать расширению кругозора;
- развивать самостоятельность и творчество, чувство отвественности, толерантности.
Тип урока: изучение нового материала.
Сопровождение к уроку: экран, проектор, компьютерная презентация, учебник Алгебра-9, автор Макарычев
Структура урока.
1. Организационный этап.
2. Постановка проблемы.
3. Актуализация знаний.
4. Исследование.
5. Проверочная работа с взаимопроверкой.
6. Проведение итогов урока.
7. Домашние задание.
8. Рефлексия.
Ход урока.
1. Организационный момент.
Приветствие учащихся, проверка их готовности к уроку.
2. Сообщение темы урока.
3. Постановка проблемы.
График квадратичной функции вокруг нас
(компьютерные презентации).
4. Актуализация знаний.
Из курса алгебры 8 класса вам знакома функция у=ах2
- что это за функция?
- что служит графиком этой функции?
- чем отличаются графики функций y=x2 и y=-x2 ; y=x2 и y=x2 ; y=x2 и y=2x2.
- сделайте вывод: на что указывает знак коэффициента “а”, значение коэффициента “а”.
Функция у=ах2 является частным случаем функции y=aх2+bx+c.
Таким образом, графиком квадратичной функции является парабола. Параболу можно встретить и в окружающем нас мире (компьютерная презентация) .
5. Исследование:
Итак, что же вы знаете пока о квадратичной функции?
Фронтальный опрос
Вместо многоточия поставить пропущенные слова
(на экране)
1. Функция вида y= ax2 + bx + c, где a, b, c-. . . , причем. . . 0, x-. . . , называется. . . функцией.
2. Функция y=x2 – это функция y=ax2 +. . . +. . . , при а=. . . , b=. . . , c=. . . .
3. Кривая, являющаяся графиком функции у=х2 называется. . . .
4. Парабола у=х2 касается оси ОХ в точке с координатами (. . . ).
5. График функции у=х2 симметричен относительно оси. . . .
6. Ось ОУ является осью. . . параболы.
7. При а. . . 0 ветви параболы у=ах2 направлены вверх, а при а. . . 0-вниз.
А теперь рассмотрим функции у=ах2 + n и у=а(х-m) 2, а именно у=х2 + 2 и у=(х-3) 2.
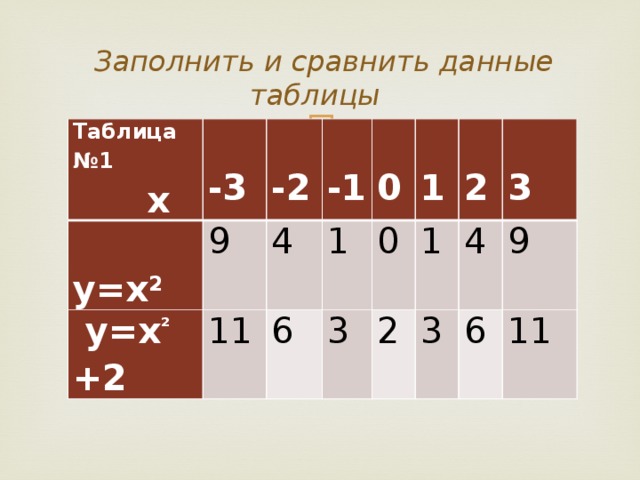
Заполнить и сравнить данные таблицы 1 (у каждого ученика на столе по 2 таблицы).
Таблица 1
Учащиеся самостоятельно заполняют таблицу, а затем проверяют по экрану
Вывод: при одних и тех же значениях х значения функции у=х2 +2 на 2 единицы больше, чем значения функции у=х2. Таким образом, график функции
у=х2 + 2 можно получить из графика функции у=х2 путем движения по оси ОY на 2 единицы вверх.
Постройте в одной координатной плоскости графики этих функций, используя шаблон параболы у=х2 (разными цветами).
Выпишите координаты вершины параболы для каждой из построенных функций.
1) (0;0) 2) (0;2)
А теперь в этой же координатной плоскости с помощью того же шаблона постройте график функций у=х2 – 2.
Сделайте вывод:
Как построить график функции у=ах2 + n при n0, при n2 ?
Далее, заполните таблицу 2
Отметьте на координатной плоскости точки, координаты которых указаны в таблице, соединив их плавной линией, получим график функции у=(х-3) 2.
В этой же плоскости постройте график функции у=х2 (с помощью шаблона)
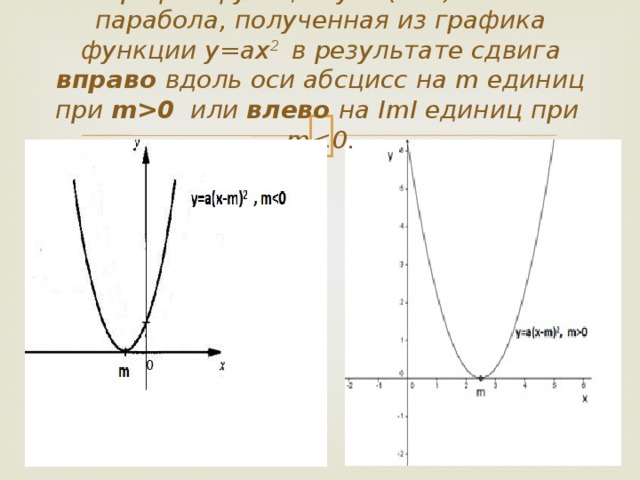
Сделайте вывод, график функции у=а(х-m) 2 есть парабола, полученная из графика функции у=ах2 в результате сдвига вправо вдоль оси абсцисс на m единиц при m0 или влево на ImI единиц при m
Координаты вершины параболы (m; 0)
А как вы думаете, что представляет из себя график функции у=а(х-m) 2 +n ?
И как можно построить график этой функции, используя сегодняшние знания?
Об этой функции и свойствах квадратичной функции будем говорить на следующем уроке, а сейчас вашему вниманию примеры зависимостей, выраженных через квадратичную функцию. Подготовленные заранее учащиеся делают краткие сообщения.
Примерами зависимости, выраженных через квадратичную функцию является:
1. Уравнение координаты тела, действующего под действием постоянной силы: Х=Х0 +V0t + a , здесь t – переменная.
2. А еще: зависимость кинетической энергии от скорости W =.
3. А еще примерами зависимости, выраженных через квадратичную функцию является:
Орбита, по которой тело будет двигаться вокруг Земли со второй космической скоростью, равной 11, 18 м/c, будет параболической.
4. А еще, тела, брошенные горизонтально или под углом к горизонту будут двигаться по параболической траектории под действие силы тяжести.
А теперь пришло время показать, чему вы научились сегодня на уроке.
6. Закрепление
106, 107, 109, 110
7. Подведение итогов урока.
Сегодня мы еще раз увидели, для чего же открыли квадратичную функцию и где можно использовать её график.
Надо помнить о том, что построение графика функции требует внимательности, аккуратности, точности в расчетах. Во всем нужен порядок. Да и математику затем учить следует, что она ум в порядок приводит.
8. Домашнее задание: №108,112, 118 (а,б)
9. Рефлексия: выходя из класса, оставьте на столе учителя одну из символов физиогностики, выражающее ваше состояние от урока.
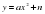 и
и 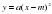 .
.







 0 или влево на ImI единиц при m " width="640"
0 или влево на ImI единиц при m " width="640"




















