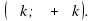МОУ лицей №10 города Советска Калининградской области
учитель математики
Разыграева Татьяна Николаевна.
Конспект урока по алгебре в 10-м классе по теме:
«Функции y = tgx, y = ctgx, их свойства и графики”.
Цели: 1. Изучить свойства функций y = tgx, y = ctgx; выработать у учащихся умения изображать схематически и читать графики этих функций. Сформировать прочные навыки в умении решать графически уравнения, выполнять преобразования графиков.
Оргмомент. Сообщение темы, целей и задач урока. Приглашение к сотрудничеству.
Актуализация знаний. Устная работа.
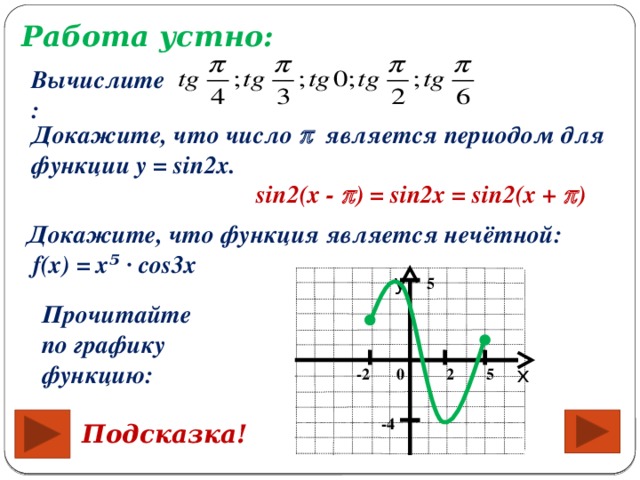
1.Вычислите: 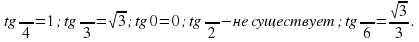
2.Докажите, что число является периодом для функции 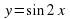 .
.
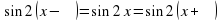
3.Докажите, что функция 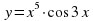 нечётная. Доказательство:
нечётная. Доказательство: 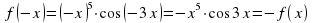 .
.
4.Прочитайте по графику функцию. 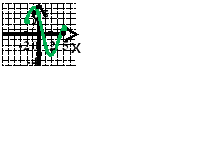
D(f) = [ -2; 5]. Функция не является ни чётной, ни нечётной. Функция возрастает на промежутках [ -2; -1], [2; 5], убывает на промежутке [ -1; 2]. Функция ограничена снизу и сверху. 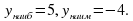 Функция непрерывна на всей области определения. E(f) = [ -4; 5].
Функция непрерывна на всей области определения. E(f) = [ -4; 5].
Изучение нового материала. Начинаем со свойств функции y = tgx. Свойство 1. Какова область определения функции y = tgx? (Все действительные числа, кроме чисел вида 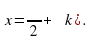

Свойство 2. Функция периодическая с периодом , т.к. 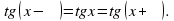
Свойство 3. Функция нечётная, т.к. 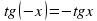 . График нечётной функции симметричен относительно начала координат.
. График нечётной функции симметричен относительно начала координат.
Составим таблицу основных значений:
| x | 0 | /6 | /4 | /3 |
| tgx | 0 | 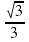
| 1 | 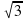
|
Построим график функции в первой четверти:
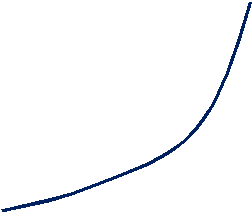
Используя свойства функции, строим полностью график функции y = tgx.
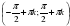
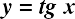
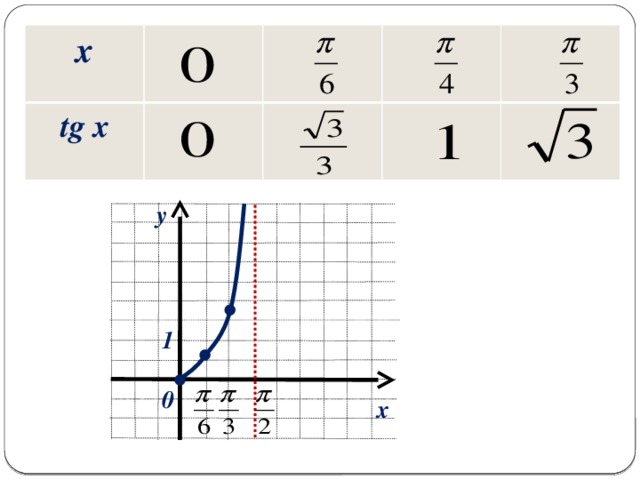
Свойство 4. Функция возрастает на всём интервале вида:
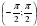 График функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.
График функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.
Свойство 5. Функция не ограничена ни снизу, ни сверху.
Свойство 6. Функция не имеет ни наибольшего, ни наименьшего значений.
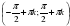 Свойство 7.Функция y = tgx непрерывна на любом промежутке вида
Свойство 7.Функция y = tgx непрерывна на любом промежутке вида
Свойство 8. E(f) = ( - ; + ).
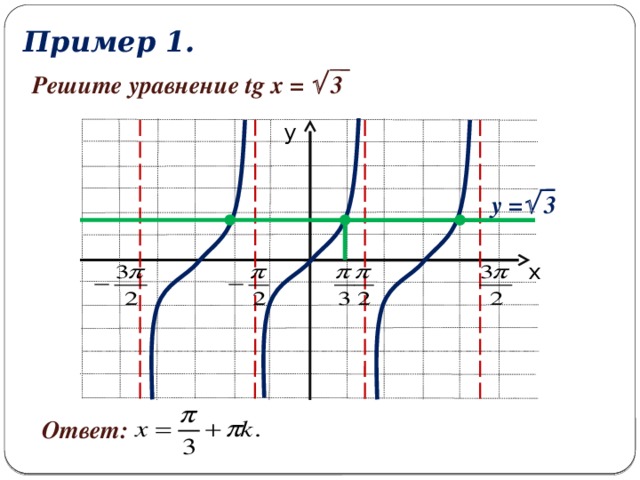
Рассмотрим пример: решите уравнение 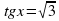 . Решим это уравнение графически. Построим в одной системе координат графики функций
. Решим это уравнение графически. Построим в одной системе координат графики функций 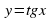 и
и 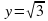 .
.

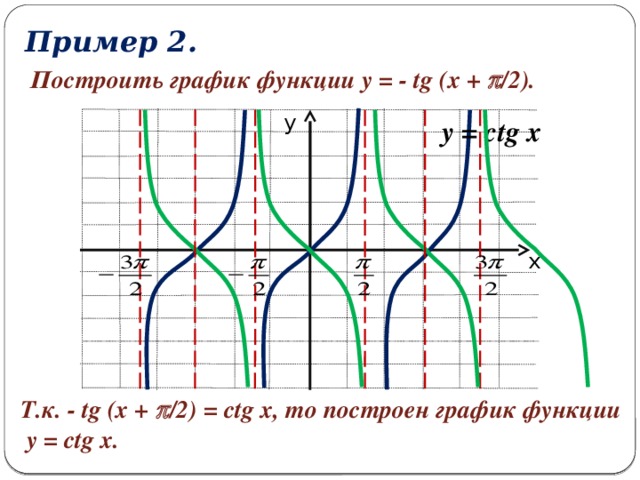
Пример 2. Построить график функции 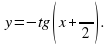
Составим план построения: 1) Построим главную тангенсоиду.
2) Отобразим эту ветвь симметрично относительно оси х. 3) Сдвинем полученную ветвь на /2 влево. 4) зная одну ветвь, построим весь график.
Т.к. 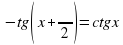 , то построен график функции
, то построен график функции 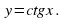
По графику полученной функции описать её свойства. Как быстро это сделать? (Большинство свойств у функций y = tgx и 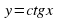 совпадают).
совпадают).
Свойство 1. D(f) – все действительные числа, кроме чисел вида x = k.
Свойство 2. Функция периодическая с периодом .
Свойство 3. Функция нечётная.
Свойство 4. Функция убывает на всём интервале вида: 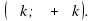
Свойство 5. Функция не ограничена ни снизу, ни сверху.
Свойство 6. Функция не имеет ни наибольшего, ни наименьшего значений.
Свойство 7.Функция y = tgx непрерывна на любом промежутке вида: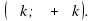
Свойство 8. E(f) = ( - ; + ).
График функции 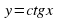 так же называется тангенсоидой.
так же называется тангенсоидой.
Закрепление изученного материала. № 254,255,257,258 – устно. № 261в, 262в – письменно.
Итог урока.
- С какими функциями мы сегодня с вами познакомились?
- Что можно сказать о них?
- Какими похожими свойствами они обладают? В чём различие?
- Как называются графики этих функций?
Домашнее задание. §15 № 256(а), 259(а), 261(а), 262(а).
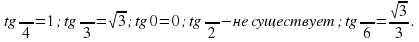
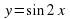 .
. 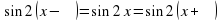
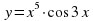 нечётная. Доказательство:
нечётная. Доказательство: 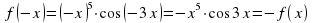 .
. 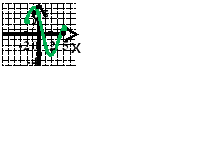
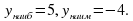 Функция непрерывна на всей области определения. E(f) =
Функция непрерывна на всей области определения. E(f) = 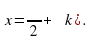

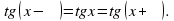
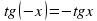 . График нечётной функции симметричен относительно начала координат.
. График нечётной функции симметричен относительно начала координат.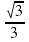
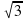

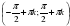
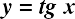
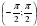 График функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.
График функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.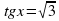 . Решим это уравнение графически. Построим в одной системе координат графики функций
. Решим это уравнение графически. Построим в одной системе координат графики функций 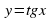 и
и 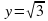 .
.
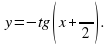
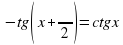 , то построен график функции
, то построен график функции 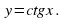
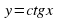 совпадают).
совпадают).